Задача о трубе

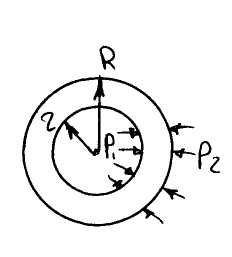
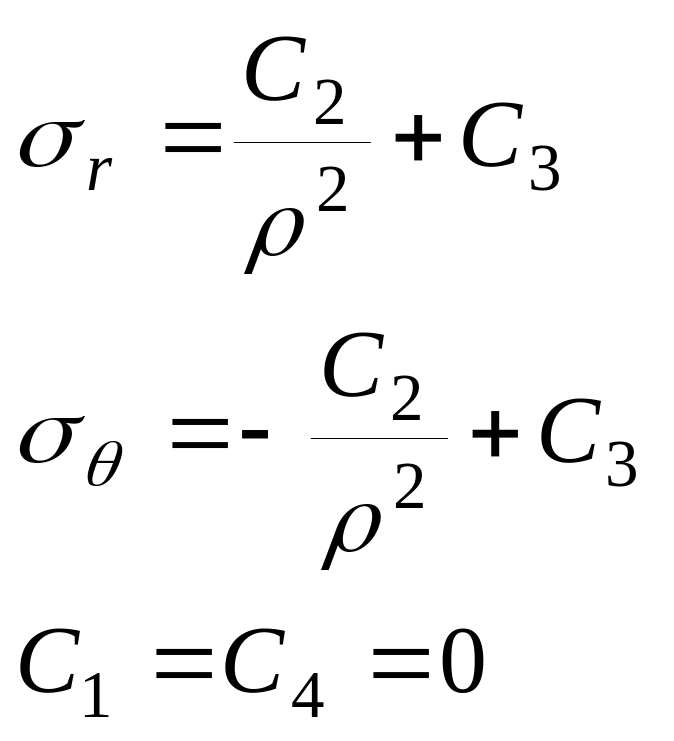
С_i – константы интегрирования уравнения

Внешнее давление:

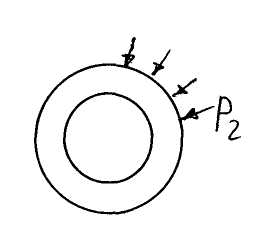
Так как R>r  C₃<0 и С₂<C₃, поэтому видно, что ₂ уменьшается к центру, ₃ наоборот увеличивается к центру, чтобы проверить на прочность надо вычислить

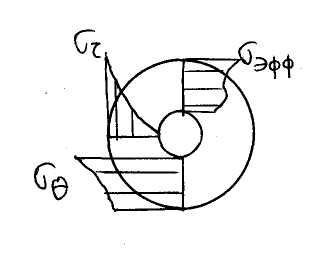
Форма кривой _эфф сильно зависит от отношения

Задача Кирша

Система уравнений в полярной системе координат позволяет легко решить и кососимметричные задачи. Одной из них является задача о растяжении пластины с отверстием (пластина считается бесконечной). Задача Кирша знаменита тем, что позволяет найти _,max . Оказывается, что _,max=3р не зависимо ни от размеров ни от упругих характеристик материала, оно возникает в точке В.

Задачи подобного типа для разных видов отверстий называются задачами о концентрации напряжений.

Следствие: при расчете даже простых с круговыми отверстиями независимо от размера отверстия мы должны уменьшать допустимое напряжение в 3 раза.

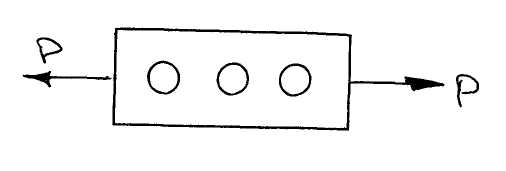
Задачи термоупругости

- закон Дюгамеля-Неймана или

Запишем обобщенный закон Гука:

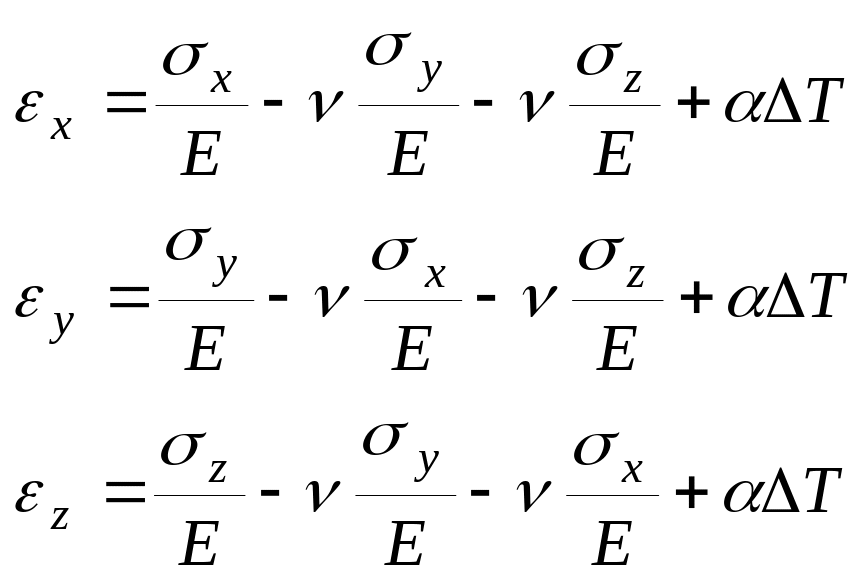
Для изотропного тела:

…

Так как Т=const , то в уравнениях внутренних элементов Т не участвует так как (Т)’=0.

Т входит только в уравнения равновесия граничных элементов и условия закрепления, если их выражаем через деформации. Аналогично задачи о трубе под давлением точное решение получено для задачи о трубе при наличии перепада температур:

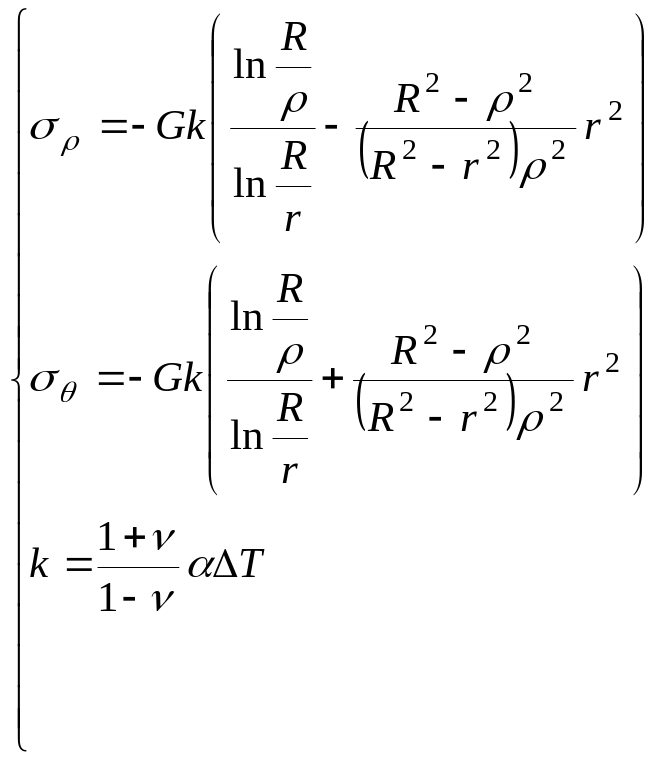
Это случай, когда нагревается наружный слой.

Примечание: в отличие от простых тел, типа параллелепипед, некоторые конструкции получают температурные напряжения с большими перепадами от сжимающих до растягивающих. Особенно большие перепады появляются в тех случаях, когда учитываются процессы теплопроводности, то есть процесс перетекания тепла из одной точки в другую, это уравнение имеет сложный вид:

,

И практически не имеет точных решений. - коэффициент отражающий способность к переносу тепла, F-внутренний источник тепла, поэтому эти задачи могут быть решены только приблизительно.