Уравнения равновесия граничных элементов

Уравнения Софи-Жермен это уравнения равновесия внутреннего элемента в виде . Кроме этого уравнения необходимо чтобы выполнялись уравнения равновесия граничных элементов. Они зависят от условий закрепления: если по краям пластина заделана, то на эти края действуют реактивные силы и записать уравнения равновесия невозможно. Можно записать только условия закрепления.

Заделка - уравнений равновесия граничных элементов нет.

Схема свободного опирания.

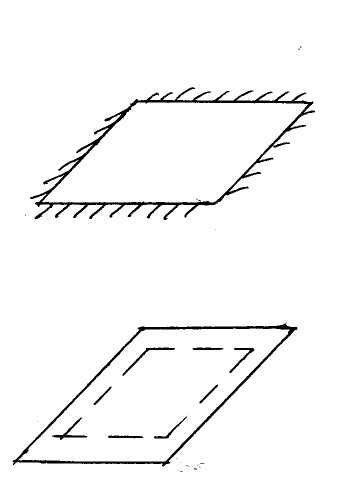
Если пластина свободно оперта по краям уравнения равновесия возможно записать.

Вырежем и рассмотрим граничный элемент, на него воздействует реактивная сила опоры.

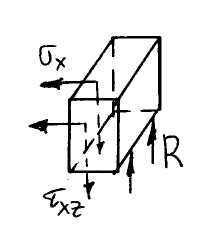
Снова видно, что условия равновесия записать в явном виде нельзя.

Составим другие условия равновесия:

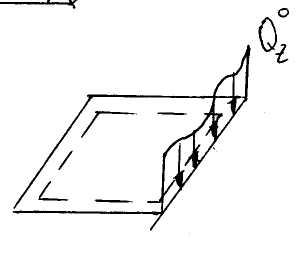
- третий случай опирания.

Рассмотрим граничный элемент:

Выражение для _xz было получено ранее:

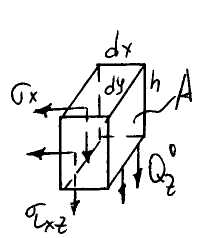
Так как выражение для _xz содержит z, то есть _xz зависти от z (переменного по высоте), поэтому его равнодействующую искать простым умножением на площадь не допустимо. Поэтому разбиваем площадь А на элементарные площадки dA, на каждой из них находим равнодействующую _xz и, суммируя, получим:

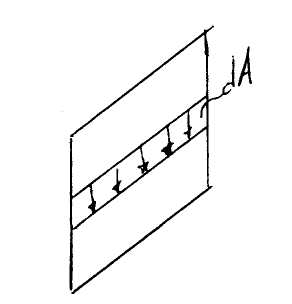
Так как при изменении у _xz почти не меняется подставляем этот результат в уравнение равновесия. Преобразуем уравнения равновесия, получим:

Подставляя сюда выражения для _xz получим алгебраическое уравнение относительно третьих производных w.

Условия закрепления

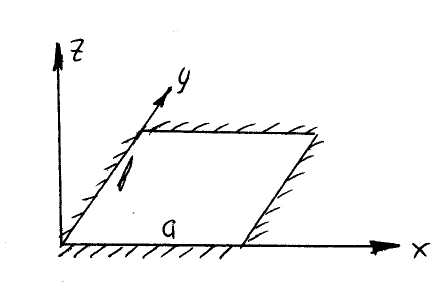
На границе w=0. Левая граница х=0 у – любая, правая х=а у – любая, передняя у=0 х – любая, задняя у=b х – любая. Кроме того угол наклона =0 на границах.

Угол наклона определяется как tg=w’_x, так как =0 w’_x=0, аналогично на передней и задней границах.

w=0 на границах w’_x0.

Точные решения задачи об изгибе жестких пластин

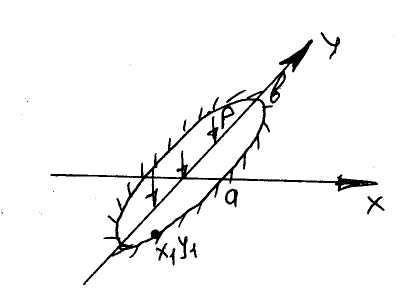
1. Решение имеет вид

Где a, b - полуоси эллипса

D – цилиндрическая жесткость пластины

B – константа, которая вычисляется из уравнения Софи-Жермен

Проверим выполнение условий закреплений :

Если взять точку на границе, то для нее выполняется уравнение эллипса подставляя это в уравнение для w, видим w=0 в точке х₁, у₁

Проверим выполнение условия w’_x=0

подставим сюда уравнение эллипса для точки х₁, у₁ получаем w’_x=0, аналогично для w’_у=0.

Найдем В из уравнения Софи-Жермен

Здесь p(x,y)=const решение можно найти только для этого случая.

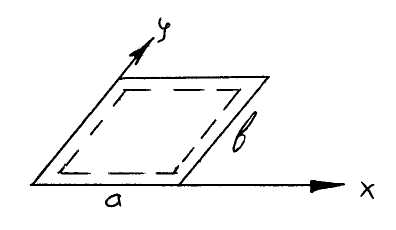
2. Задача о свободно опертой прямоугольной пластине под нагрузкой образованной сыпучим материалом. Оказалось, что из всех аппроксимаций нагрузки от сыпучего материала наиболее удачной является следующая:

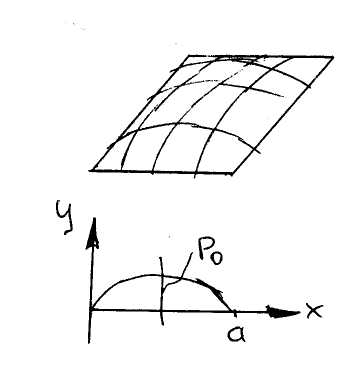
Запишем уравнение Софи-Жермен:

Очевидно, что w надо искать в виде:

В результате получим:

Проверим выполняются ли условия закрепления и уравнения равновесия граничных элементов:

- на границе

Условия закрепления выполняются на правом краю х=а σ_х=0 при любом у

При х=а отсюда σ_х0. Аналогично на других границах и уравнения равновесия граничных элементов выполняются.

Так как все уравнения и закрепления выполняются, то решение точное.

Решение задачи изгиба пластины свободно опертой по краям при произвольной нагрузке Р (метод Бубнова-Галеркина):

Подставляя, получим:

для получения алгебраических уравнений относительно В₁₁,В₂₂… можно использовать любые методы (коллокаций), но наиболее удобным является метод Бубнова-Галеркина. Причина в том, что в методе Бубнова сразу получаются выражения для B_ij.

Умножим это уравнение на , проинтегрируем по площади пластины:

Справа получим:

Рассмотрим левую часть:

Оказывается, что все слагаемые кроме первого равны нулю, причем

Таким образом получаем:

Остальные коэффициенты получаются аналогично.