Функция напряжений (Эри)

Применяется для решения плоской задачи теории упругости.

Суть этой функции в замене трех искомых напряжений одной искомой функцией.

Функция вводится следующим образом:

Для случая, когда q_x=q_y=0 подставляем в уравнения равновесия внутреннего элемента:

Таким образом, уравнения равновесия внутреннего элемента удовлетворять уже не надо, так как они выполняются тождественно. Остается выполнить уравнения равновесия граничных элементов, условия совместности деформаций или закон Гука и соотношения Коши.

Теории изгиба жестких плит

Плита называется жесткой, если ее прогибы малы по сравнению с толщиной. Если прогибы велики, то при жестком закреплении кромок появляются силы растяжения плиты, так как размеры плиты по ширине увеличиваются, что означает наличие сил растяжения.

Решение ищется в перемещениях:

Разложим функции в ряд Маклорена:

Из анализа картины деформаций элемента плиты можно заключить, что точки срединной поверхности в плоскости пластины не перемещаются (срединная поверхность z=0).

Так как толщина плиты мала, то z тоже мал, поэтому можно написать, что:

Эти упрощенные соотношения называются гипотезами Кирхгоффа-Лява (геометрические гипотезы).

Для дальнейшего упрощения u_x1, u_y1 выражают через u_z0 из геометрических соображений.

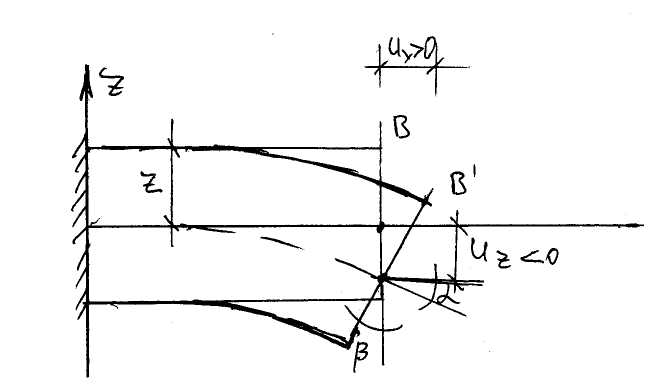
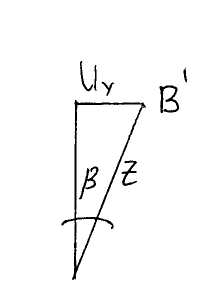
Из рисунка видно, что =, так как это углы с перпендикулярными сторонами.

Так как

Согласно гипотезам Кирхгофа-Лява:

Аналогично (так же из гипотезы Кирхгофа-Лява)

И формулируется: нормаль остается нормалью, и после деформации

Для простоты вводятся обозначения: через w обозначают u’_zo(x,y), тогда:

Таким образом перемещения любой точки пластины нам известны, тогда можно вычислить деформации по соотношениям Коши, а затем напряжения по соотношениям закона Гука:

Остальные деформации:

Эти соотношения примерны, так как мы оборвали ряд Маклорена, на самом деле деформации по z существуют.

Кирхгоф и Ляв приняли следствие как гипотезу и на сегодня они звучат следующим образом:

- поперечных деформаций нет

Это предположение является противоречивым, так как при продольном растяжении-сжатии элемента тела появляются поперечные деформации в виду эффекта Пуассона, но в совокупности, в целом для тела, это соотношение является справедливым.

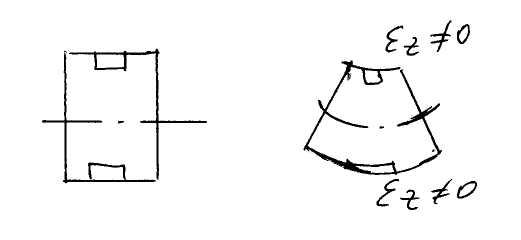
Второе противоречие:

Но это полное противоречие формуле Журавского, согласно ей

Это противоречие есть следствие приближенности выражений для перемещений (оборван ряд Маклорена). Как показали эксперименты, и точные решения на максимальные напряжения они не влияют.

Вывод уравнения для определения функции w

Используем следующие выражения:

Используем закон Гука:

Теоретически было доказано, что:

и аналогично

- статические гипотезы Кирхгофа-Лява. (Проверку их для балки смотри в предыдущей лекции)

Воспользуемся первым соотношением из статических гипотез, получим:

Но в уравнениях равновесия σ_z,_yz,_xz отбрасывать нельзя, поскольку производная это тангенс угла наклона, то даже при малости функции угол её наклона может оказаться очень большим.

Из закона Гука легко найти σ_х:

_х и _у выразим через w и получим:

Для изотропного материала , тогда , подставим это в первые два уравнения равновесия. После подстановки получим:

, отсюда можно найти _xz, _yz:

Для отыскания ₁, ₂ используем уравнения равновесия граничных элементов

При z=

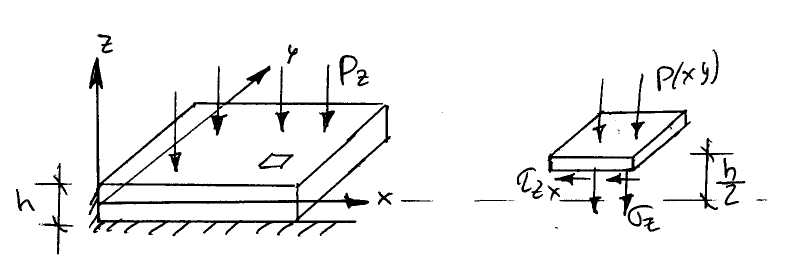
Подставим в полученные уравнения:

Аналогично из уравнения равновесия другого граничного элемента получаем:

Проверим выполняются ли уравнения равновесия граничных элементов, которые примыкают к нижней грани, где z=- , здесь z²= , поэтому уравнения равновесия выполняются автоматически.

Удовлетворим третье уравнение равновесия:

подставим сюда выражения для _xz, σ_yz с учетом ₁, ₂

Найдем σ_z, проинтегрировав это уравнение:

Как и ранее ψ(х,у) определяем из уравнений равновесия граничных элементов:

Из второго условия получим:

Введем обозначение: - цилиндрическая жесткость

Уравнение для w получим из условия при

- уравнение Софи-Жермен (получено в 1816 году).

Достоинства и недостатки полученной теории пластин:

• Нужно находить только одну функцию w, через нее вычисляются все деформации и напряжения

• w имеет физический смысл – это прогиб пластины, поэтому можно решение отыскивать по экспериментальным данным

• согласно теории _z=0 так как , из положения выходят с помощью закона Гука: , поэтому _z можно вычислить

• это противоречие решается с помощью уравнений равновесия , - это аналоги формулы Журавского

• При подсчете реактивных сил шарнирно опертой пластины в углах расчеты дают сосредоточенные силы, так как сосредоточенных сил в природе не существует, то это противоречит основам теории упругости, теория Кирхгофа-Лява позволяет получать хорошие решения только внутри области пластины, вблизи края решение может сильно отличаться от истинного, поэтому использовать решение задачи о пластине в рамках гипотез Кирхгофа-Лява не допустимо для расчета опор пластины

• Возникают трудности при формулировке уравнений равновесия граничных элементов, примыкающих к торцам пластины