Метод Бубнова-Галеркина
Как и в методе коллокаций решение ищется в виде аппроксимации с неизвестными коэффициентами, то есть :
Аналогично находятся
деформации и перемещения:
.
Напряжения подставляются в уравнения
равновесия внутреннего и граничных
элементов, перемещения подставляются
в условия закрепления. В результате
получаем не алгебраические, а функциональные
уравнения.
Уравнения равновесия внутреннего элемента:
F(a00, …, х)=-q(x)
Уравнения равновесия граничных элементов:
H (a00,… х)=p(x)
Условия закрепления:
G (a00, …, х)=0
Слева и справа в этих уравнениях функции близки друг к другу, значит и интегралы от них должны быть почти одинаковы
Исходные уравнения можно умножать на любую функцию, от этого равенство не изменится, после этого можно интегрировать еще раз
…
Недостаток метода
в том, что
,
…
выбираются расчетчиком, следовательно
решение достаточно субъективно, однако
математиками доказано, что, как правило
наилучшее приближение к точному решению
получается тогда, когда в качестве
,
…
берутся функции использованные для
аппроксимации перемещений.
Рассмотрим пример:
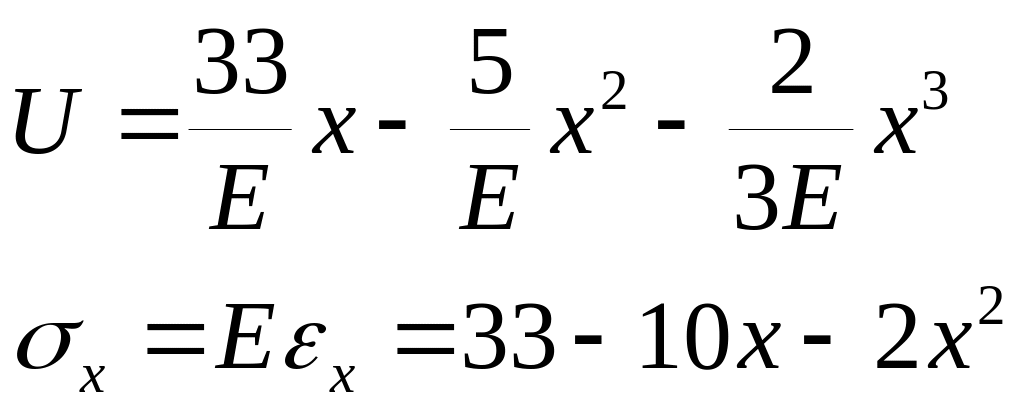
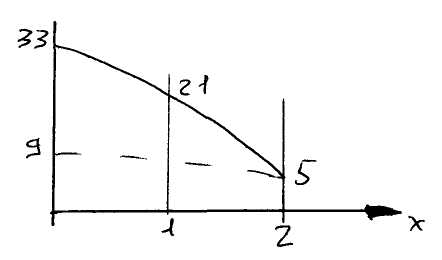
Опосредованная оценка точности решения
Для оценки вычисляют потенциальную энергию системы:
PU – работа внешних сил на перемещениях системы.
Первое слагаемое – энергия деформации, если окажется, что первое решение дает П1, а второе П2, причем П1>П2, то скорее всего второе решение более точное.
В теории упругости хорошим будем называть решение, которое ближе к точному по максимальным напряжениям. Под максимальным напряжением понимается обычно эффективное напряжение (эквивалентное, приведенное). Для плоской задачи, согласно Четвертой теории прочности:
Доказательство:
Пусть точное
решение U=Uточное
, тогда
Тогда приближенное
решение U=Uточное+ΔU,
тогда
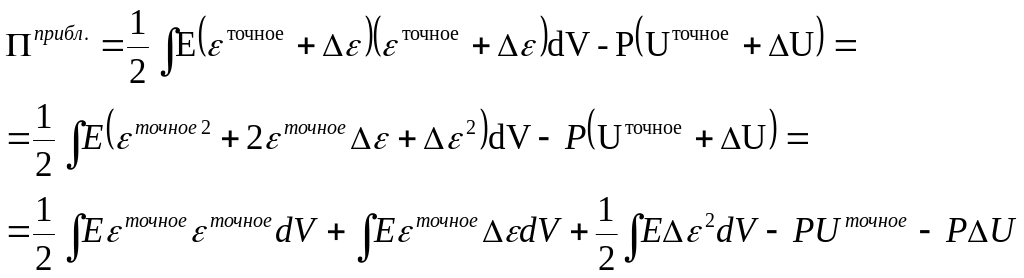
В силу принципа Лагранжа (возможных перемещений):
в результате
получаем:
Таким образом для точного решения П всегда меньше чем П для приближенного.
Типы плоских задач теории упругости
Существует два типа плоских задач:
Плоское напряженное состояние (ПНС)
Плоское деформированное состояние (ПДС)
ПНС возникает в тонких плитах, балках-стенках, оболочках.
Здесь принимают:
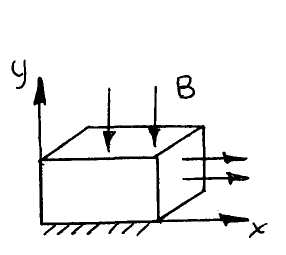
На первый взгляд
кажется, что и в поперечном направлении
напряжения должны быть большими, но
многочисленные теоретические и
экспериментальные исследования показали,
что в действительности:
и
Рассмотрим пример:
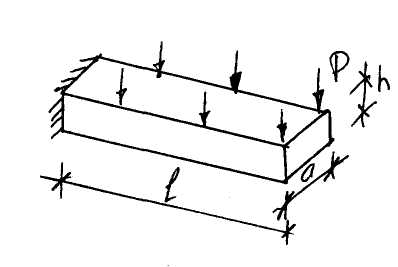
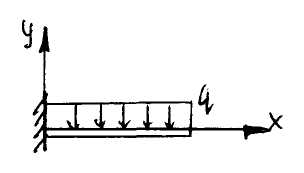
Для этого случая существует решение сопротивления материалов
Переходим к другой схеме:
Примем сечение балки квадратным a=h, тогда:
Рассмотрим эту задачу с точки зрения теории упругости:
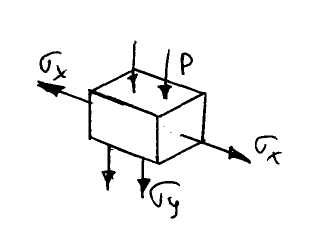
Рассмотрим элемент:
Сравним полученные результаты:
При l/h>>1,
то
,
отсюда
Пусть l=100см
h=10см,
тогда
Таким образом, поперечные напряжения в 300 раз меньше продольных максимальных напряжений.
Плоское деформированное состояние (ПДС) возникает в телах типа дамбы, ленточного фундамента, дорожного полотна…
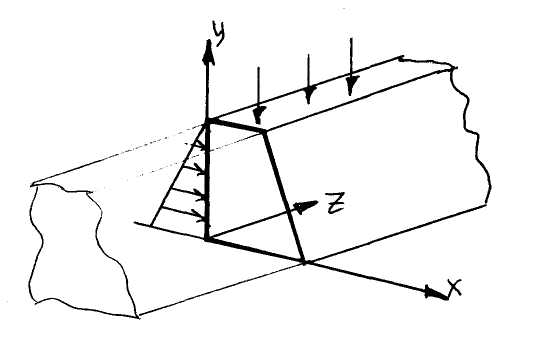
Здесь
,
в этих телах
;
;
,
так как здесь деформации нулевые, то
это состояние называется плоским
деформированным состоянием.
Однако, для обоих типов разрешающие уравнения имеют одинаковый вид, отличие состоит лишь в законе Гука.
В обоих случаях yz=0 или yz=0 соотношения выполняются одинаково.
Для граничных элементов уравнения равновесия также не отличаются.
Рассмотрим закон Гука
ПНС:
Из первых двух выражений находим напряжения через деформации, таким образом, закон Гука при этом сильно упрощается.
ПДС:
Таким образом зная σх и σу легко найдем σz. Выразим x, y через σx, σy
По аналогии получим:
Введем приведенные модуль Юнга и коэффициент Пуассона:
Таким образом, закон Гука для ПДС принимает вид:
То есть имеет такой же вид, как и в ПНС.