Метод коллокаций

Суть метода- искомые напряжения представляются в виде суммы функций с искомыми коэффициентами. Например:

Функции при коэффициентах выбираются на усмотрение того, кто вычисляет, из соображений простоты или точности.

a_ij; b_ij; c_ij – отыскиваются из уравнений равновесия

Уравнения равновесия внутреннего элемента:

Подставляем сюда заданные нами функции для σ_x, τ_xy, σ_y :

Получаем два уравнения относительно искомых коэффициентов.

Обеспечить выполнение этих уравнений во всех внутренних элементах не представляется возможным, поэтому удовлетворяем их только в некоторых элементах – точках коллокации. Точками коллокации называются координаты бесконечно малых элементов, в которых мы удовлетворяем уравнении равновесия. Самыми удобными функциями являются степенные функции.

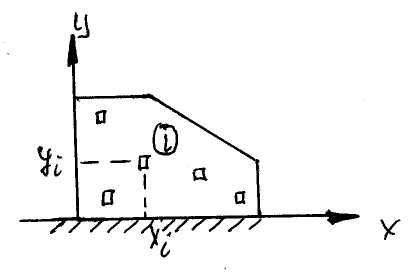
Кроме внутренних элементов аналогичным образом только в некоторых элементах выполняются граничные условия, то есть уравнения равновесия граничных элементов.

Число всех уравнений должно быть равно числу всех неизвестных коэффициентов.

Пример:

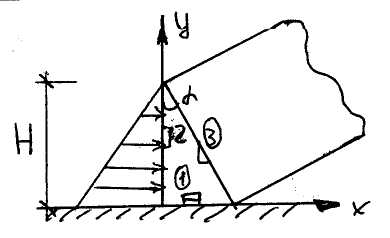
Решение ищем в виде:

a_ij=?; b_ij=?; c_ij=?

Из уравнений равновесия внутреннего элемента получаем:

Из уравнений равновесия элемента на левой грани:

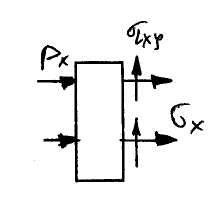
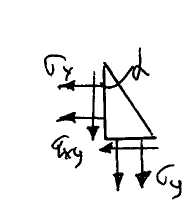
Из уравнений равновесия элемента на наклонной грани:

Получаем решение задачи о дамбе:

Аналогично определяются уравнения для отыскания оставшихся неизвестных из второго уравнения.

Выводы из решения:

• Решение имеет очень простой вид

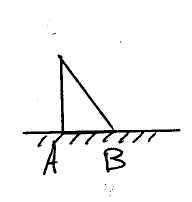
• Это решение не может удовлетворить условия закрепления основания:на линии АВ _х=0 по закону Гука: (если подставить вычисленные значения напряжений), если нас не интересует точность решения в опорной зоне, то решение приемлемо. Однако это противоречие не является столь существенным, так как условие жесткой заделки обеспечить невозможно. Все недостатки решения сглаживаются введением коэффициента запаса.

Решение задач теории упругости при наличии ограничений на перемещения

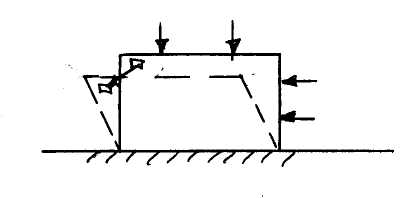
Рассмотри деформации балки-стенки под действием некоторой нагрузки. - вектор перемещений. Так как разные элементы перемещаются по разному, - зависит от координат элемента (его положения): = (х, у, z)

По закону параллелограмма мы можем рассматривать не вектор, а его компоненты.

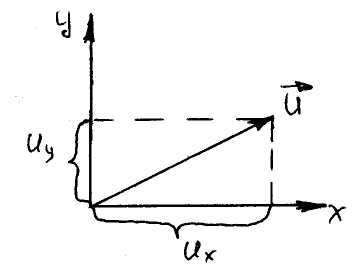
Соотношения Коши

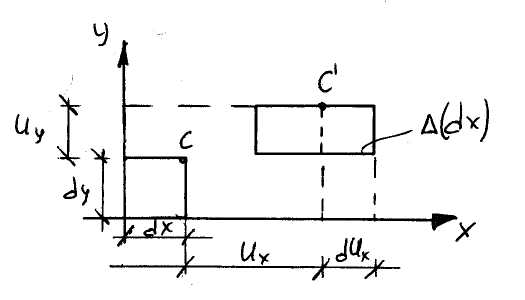
- первое соотношение Коши

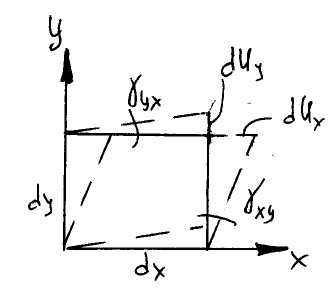
В силу малости угла  : , даже при =30⁰ погрешность составляет около 5%.

Аналогично .

При вычислении деформаций наибольшее значение имеет суммарное изменение угла:

Обобщенный закон Гука

Следствие из соотношений Коши

Оно ограничивает применение метода коллокаций (условие совместности деформаций)

Подставляя сюда ,_х, _у по закону Гука получим связь:

Таким образом выбирать аппроксимации для напряжений произвольным образом нельзя, так как должны выполняться условия совместности деформаций.

Вторая краевая задача теории упругости

Если не нужно выполнять условия закрепления конструкции, то задача называется первой краевой задачей теории упругости.

Если тело закреплено со всех сторон (если заданы перемещения границы), то задача называется второй краевой задачей теории упругости.

Если часть края конструкции закреплена, а другая часть свободна, то задача называется смешанной краевой задачей теории упругости.

Методика решения задач при наличии закреплений:

1. Перемещения задаются в виде аппроксимаций с неизвестными (искомыми) коэффициентами. Например:

2. Записываются выражения для деформаций:

3. Находим выражение для напряжений:

Знаменатель (1-²) появляется тогда, когда определяем σ_х, σ_у через _х, _у.

4. Соотношения пункта 1. подставляются в условия закрепления, а соотношения из пункта 3. в уравнения равновесия. Получается система уравнений, которая содержит искомые коэффициенты, а также функции х,у,х²,у²…

5. Выбирается какой либо метод, который позволяет исключить х,у и их функции из полученной системы.

Задача: растяжение балки-стенки

q_x=2x², p₀=5, =0

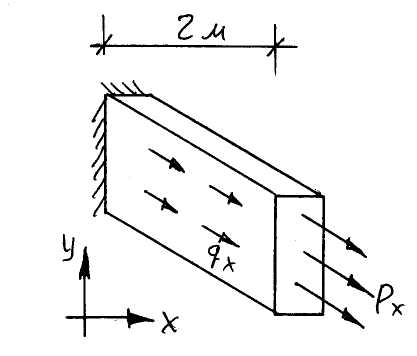
Решение:

Видно что σ_у в нашей задаче равно нулю (σ_у=0), так как =0, также отсутствуют сдвиги τ_ху=0.

Получаем уравнения равновесия в виде:

для внутреннего элемента

при х=2 – для краевого элемента

Зададим условия закрепления при х=0 U_x=0

1. 

2. 

3. 

4. 

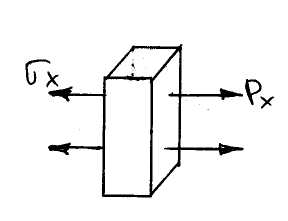
5. Используем метод коллокаций для получения алгебраической системы:

Выберем элементы коллокации

х₁=0

х₂=2

Таким образом:

Построим эпюру напряжений по длине.

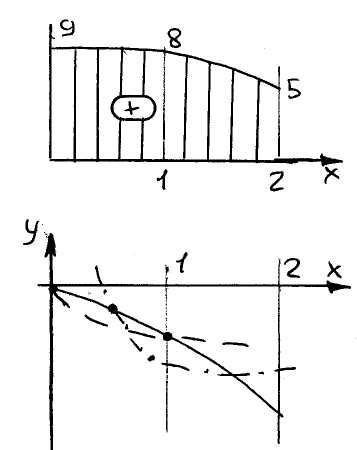
Недостатки метода коллокаций:

• Решение сильно зависит от точек коллокации, если брать число искомых коэффициентов не очень большим (23)

Второй вариант точек коллокации:

При х₁=0

Из уравнения равновесия граничного элемента:

Теперь решение принимает вид: