Теория упругости Ведение

Предмет теории упругости – это наука, которая занимается вопросами прочности, жесткости и устойчивости упругих тел произвольной конфигурации (балки-стенки, плиты, стыковые узлы – характерны для строительства).

Законы, используемые в теории упругости.

Статическая теория упругости использует следующие законы механики:

1. Уравнения равновесия

2. Закон Гука, который предполагает линейность, то есть прямо пропорциональную зависимость деформаций от нагрузок.

3. Закон сохранения энергии.

4. Закон Дюгамеля-Неймана (закон линейного температурного расширения)

Основное отличие теории упругости от сопротивления материалов заключается в следующем: в сопротивлении материалов используется метод сечений, в котором конструкцию делят на две части. Воздействие одной части на другую заменяют (изображают) силами и моментами. Эти воздействия находятся из условия, что любая часть конструкции находится в покое.

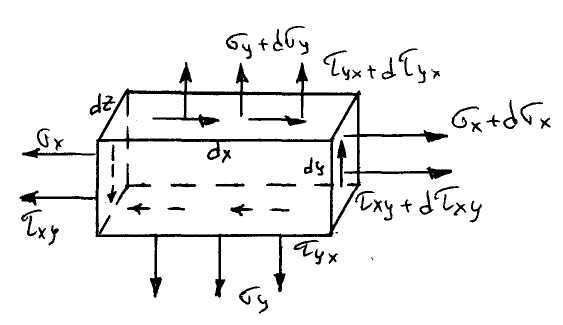
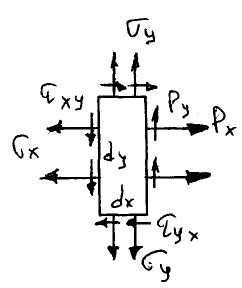
В теории упругости сечениями из конструкции выделяется микроэлемент, на него со всех сторон воздействуют соседние элементы силами σ_х, σ_у распределенными по поверхности.

Для этого элемента составляются уравнения равновесия. Совокупность таких уравнений для всех микрочастиц и является объектом изучения теории упругости.

Уравнения равновесия

Уравнения равновесия внутреннего малого элемента.

– малая величина, на которую различаются напряжении на правой и левой гранях элемента

– первый индекс в обозначении касательных напряжении показывает площадку, на которой действует напряжение, второй индекс показывает направление.

Как частица всего тела этот элемент находится в покое, поэтому можем записать уравнения равновесия.

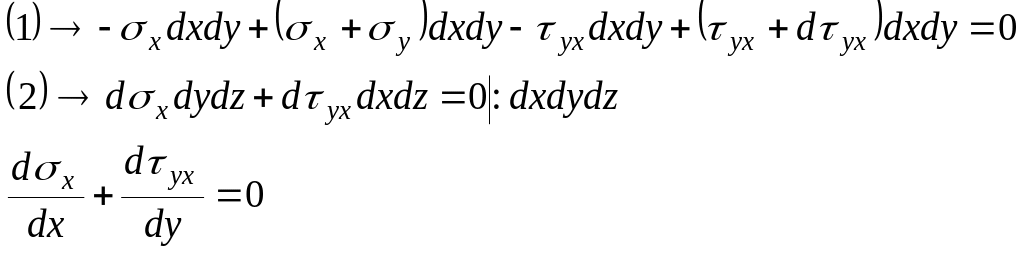
Обобщения:

1. Если имеется воздействие по оси z, то в уравнение добавляется еще одно слагаемое .

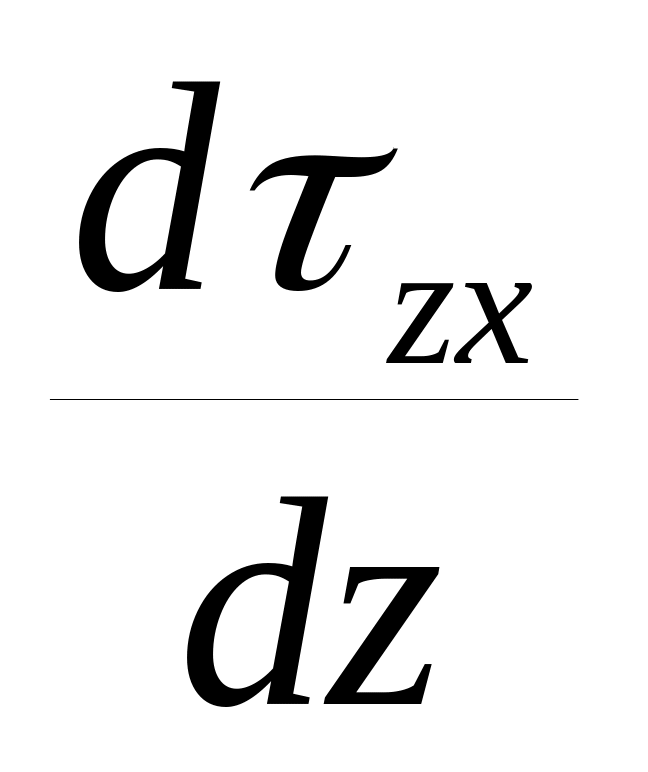2. На тело кроме поверхностных внешних сил действуют объемные силы (собственный вес в строительстве, силы инерции в динамике)

Рассмотрим эти силы:

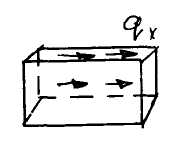
Вес параллелепипеда с удельным весом q_x ,будет:

Поэтому в уравнение равновесия добавится удельный вес.

Таким образом в общем случае уравнении равновесия имеют следующий вид:

Это дифференциальные уравнения равновесия внутреннего микроэлемента (уравнения в приращениях).

В строительстве, как правило, σ_z, τ_yz, τ_xz – очень малы, поэтому в дальнейшем будем использовать следующую систему

Эта задача может быть решена в предположении, что все внешние воздействия известны, но чаще всего реакции опор неизвестны или их трудно найти.

Этих уравнений бывает достаточно для определения σ_х, σ_у, τ_ху, если известны все активные и реактивные силы и известны уравнения равновесия граничных элементов.

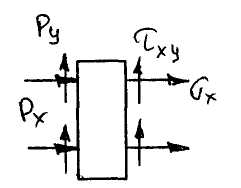
Уравнения равновесия граничного элемента

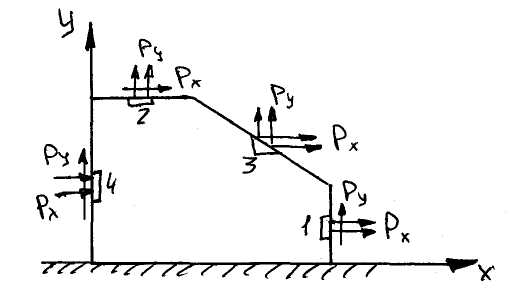
Если p_x<0, то p_x действует против оси х. Усилия всегда изображаются по оси х, если необходимо указать, что оно действует против оси, ставят знак “ – “.

Рассмотрим

Малые элементы, примыкающие к границе:

Для упрощения выкладок считаем, что , то есть d_x по сравнению с d_у бесконечно мал тогда вкладом напряжений на горизонтальных площадках можно пренебречь.

На правой грани в состоянии покоя должны выполняться такие условия:

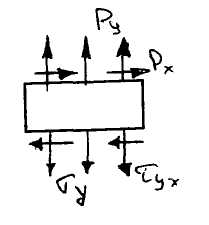
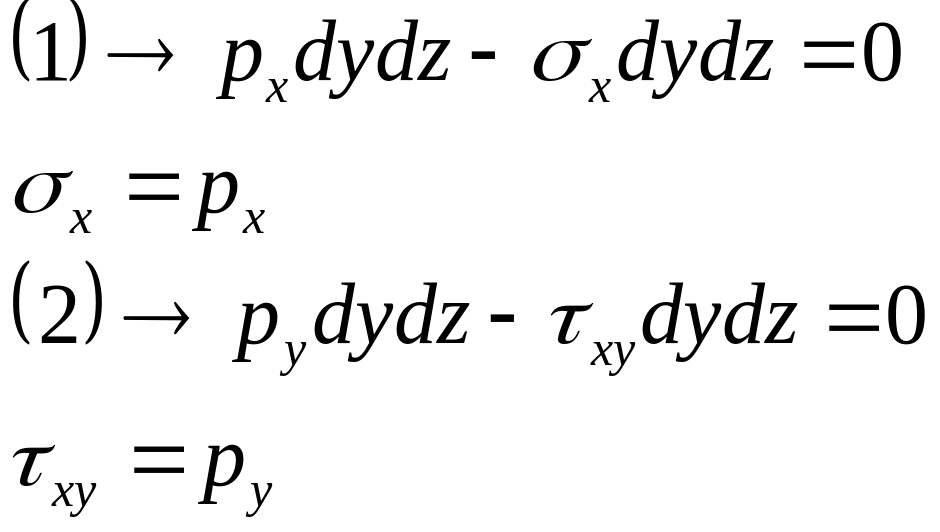
По аналогии получаем уравнения равновесия элемента расположенного на верхней грани:

Уравнения равнения равновесия элемента расположенного на наклонной грани:

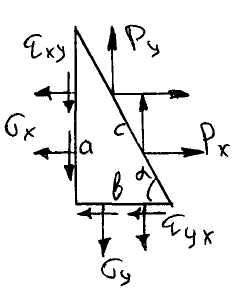
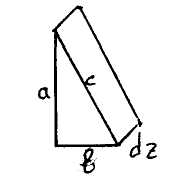
Уравнения равнения равновесия элемента расположенного на левой грани:

Правила для изображения направления напряжений

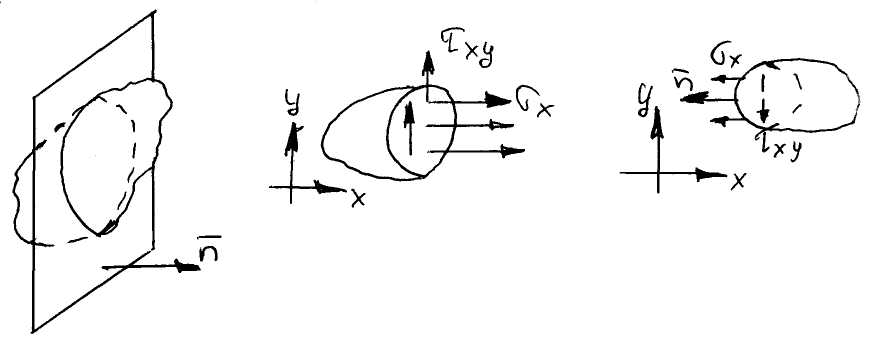
Нормаль направлена в ту сторону тела, часть которого действует на рассматриваемую часть ( в сторону отброшенной части). Если направление нормали совпадает с осью Х, то σ_х, τ_ху, направлены в положительном направлении осей, если нет, то напряжения направлены в обратную сторону.