7. Примеры решения задач
ЗАДАЧА 1. Определить индукцию магнитного поля в центре проволочной квадратной рамки со сто-роной а, если в рамке течет ток I.
Дано: Решение
а, I a2 =180o − a1
В = ? a2
J
a1
a
r
B
В = 4В1
1 = µ0 ×I × cosa1 −cosa2 ) 4pç 2ø
B = 4× æ I ö ×2cosa1
è 2ø
ЗАДАЧА 2. По двум бесконечно длинным прямым параллельным проводникам, расстояние между ко-торыми d, текут токи I1 и I2 в противоположных направлениях. Определите магнитную индукцию В в точке А, удаленной на расстоянии r1 от первого и r2 от второго проводника.
37
Дано: Решение
I1, I2, d,
B2
в b = 180º – a B
a r2
1
r
r
r
=
,
B
1
p
2
r
1
r
+В
2
В
В
1
r r
2
(
)
1 2
p
2
2 2 2
2
1
1
1
2
R
2
p
m
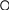
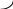
r1
B
I2
I1 d r1, r2
B = ?
µ0I1 1 2pr
B2 = µ0I2 . B = B + B2. 2
Результирующую магнитную индукцию найдем по теореме косинусов: В = 12 22 +2В 2 cosb, cosa = 12 +r 2 −d2 ,
1 2
B = µ0 × I12 + I22 − I1I2 × r 2 + r 2 −d2 .
r r r r
ЗАДАЧА 3. Напряженность Н магнитного поля в центре кругового витка с магнитным моментом pm =1,5A×м2 равна 150 А/м. Определите: 1) радиус витка; 2) силу тока в витке.
Дано: Решение
Н = 150 А/м pm =1,5 А·м2
H = I ; pm = I ×S = IpR2 = H ×Ip2R3,
R = ?
I = ?
откуда R = 3 H × I ×2p =11,7×10−2 м,
I = H ×2R =35,1 А.
ЗАДАЧА 4. Бесконечно длинный провод образует круговую петлю, касательную к проводу. По прово-ду идет ток силой I. Найти радиус петли, если известно, что напряженность магнитного поля в центре пет-ли равна Н.
Дано: Решение
H, I I
R = ?
0
R
I
38
По принципу суперпозиции полей:
H = H1 + H2 = I + 2I = I æ1+ 1 ö = I ×0,66 A/м ,
откуда R = I ×0,66.
ЗАДАЧА 5. Между полюсами магнита на двух тонких нитях подвешен горизонтально линейный про-водник весом Р = 0,1 Н и длиной l = 0,2 м. Напряженность однородного магнитного поля Н = 2×105 А/м и направлена вертикально. Весь проводник находится в магнитном поле. На какой угол a от вертикали от-клонятся нити, поддерживающие проводник, если по нему пропустить ток I = 2 A? Весом нитей пренеб-речь.
Дано: Решение
)
(
ç
÷
pR
p
2
2
R
R
R
ø
è
H
r
r
T
A
F
A
Р
Р
r
r
В
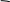
Р = 0,1 Н l = 0,2 м
Н = 2×105 А/м
I = 2 A FA
a = ?
T a a
I
Сила Ампера FA = B× I ×l
B p
Условие равновесия проводника:
r+ FA + P = 0, т. е.
T sina = F , T cosa = Р,
или
tg ×a = Р = BI ×l = µ0HI ×l »1, тогда
a = 45o.
ЗАДАЧА 6. a-частица, момент импульса которой L =1,33×10−22 кг ×м2/с, влетает в однородное маг-
нитное поле, перпендикулярное скорости ее движения. Индукция магнитного поля равна 2,5×10−2 Тл. Най-ти кинетическую энергию a-частицы.
Дано: Решение
L =1,33×10−22 кг×м2 /с B = 2,5×10−2 Тл
B ^ v
q v
Fл
q =3,2×10−19 Кл r m = 6,64×10−27 кг
ЕК = ?
На заряд, движущийся в магнитном поле, действует сила Лоренца, которая выполняет роль центрост-ремительной силы:
39
Bqv = m×v2 ,
откуда
R = m×v.
L = mvR = mv× Bq = Bq ×mv2,
mv2 = L×B×q ,
следовательно,
mv2 L×B×q 1,33×10−22 ×2,5×10−2 ×3,2×10−19 k 2 m×2 6,64×10−27 ×2
=0,8×10−16 Дж =500эВ.
ЗАДАЧА 7. Тонкий медный провод массой m = 1 г согнут в виде квадрата, и концы его замкнуты. Квад-рат помещен в однородное магнитное поле (В = 0,1 Тл) так, что плоскость его перпендикулярна линиям ин-дукции поля. Определить количество электричества, если квадрат, потянув за противоположные вершины, вытянуть в линию.
R
Bq
m
mv
m
=
=
= =
E
1
dt
e
i
dt
dq
Ф
d
d
Ф
1
,
Ф
R
1
1
1
1
R
m
S
1
S
S
2
×
×
S
B
Bm
m
1
1
r×
r×
4
S
a
1
1
Дано:
m =10−3 кг В = 0,1Тл,
r =8600кг/м3
r =1,7×10−8 Ом×м
q = ?
Решение
Согласно закону Фарадея для электро-магнитной индукции:
ei = − dФ.
По закону Ома для полной цепи I = R , где I = dq,
dt R = − dt , dq = − R × dt . (1)
Выражение (1) проинтегрируем:
q = − 1 ×( 2 −Ф1)
где Ф2 =0, Ф = В×S.
q = B×S , m = r ×V = r ×4a×S ,
где S1 – площадь поперечного сечения проводника; а – сторона квадрата; r1 – плотность меди; V – объем проводника.
a = r ×4 1 . Сопротивление
R = r×l = r×4a ,
1 1
где r – удельное сопротивление.
q = B×a4×S = B×a×S = r×4×r1×4× 1 = 16×r×r = 42,7×10−3 Кл.
40
ЗАДАЧА 8. В однородное магнитное поле напряженностью Н помещена квадратная рамка со стороной а. Плоскость рамки составляет с направлением магнитного поля угол a. Определить магнитный поток, пронизывающий рамку.
Дано: Решение
Н, а, a r – нормаль к рамке. H Магнитный поток
n
n
r
1
dF
p
х
2
µ
µ
r+l
I I
I I
dх
−
7
F
1
2p
2p
х
r
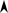
Ф = ?
a r
Ф = BS cosa,
где
B = µ0H, S = a2, тогда
Ф =µ0а2Н cosa.
ЗАДАЧА 9. Металлический стержень длиной 15 см расположен перпендикулярно бесконечно длинно-му прямому проводнику, по которому течет ток силой 2 А. Найти силу, действующую на стержень со сто-роны магнитного поля, создаваемого проводом, если по стержню течет ток силой 0,5 А, а расстояние от провода до ближайшего конца стержня 5 см.
Дано: Решение
I1 = 0,5 A I2 = 2 A
r = 0,05 м
F1 = ?
I2
B2 B2
r C
dF
dх I1 D
х
Разобьем проводник СD на малые элементы длиной dх, находящиеся на произвольном расстоянии х. По закону Ампера на каждый элемент dх действует сила 1 = I1B2 ×dх, где
B2 = µ0I2 .
Полная сила
r+l r+l
1 = òdF = 0 2 1 ò = 0 2 1 ×ln = 2,8×10 H. r r
ЗАДАЧА 10. На графике изображена зависимость магнитного потока, пронизывающего катушку, от времени. Построить график зависимости ЭДС индукции от времени.
Ф
0 t1 t2 t
41
Решение
Ф
t1 t2 t
ei
0 t
На участке ott ∆Ф > 0, то ei < 0; на участке t1t2 ∆Ф < 0, то ei >0.
ЗАДАЧА 11. В вертикальном однородном магнитном поле с индукцией В вращается в горизонтальной плоскости стержень длиной l с постоянной угловой скоростью w. Ось вращения проходит через конец стержня. Определить в стержне ЭДС индукции.
∆
t
∆
t
Ф
∆
t
t
p
2
2
2
=
=
1
W
.
,
W
2
2
I
1
2
W
2
2
−
I
2
Дано:
B, l, w
ei =?
Решение
ei = − ∆ t = B×S ×N ,
где N – число полных оборотов.
n = N – частота вращения; w = 2pn.
ei = B×p×l2 ×w = Bw×l2 .
ЗАДАЧА 12. Определить индуктивность длинного соленоида, в котором при увеличении тока от I1 = 4 А до I2 = 6 А энергия магнитного поля увеличивается на ∆W = 10 мДж.
Дано:
I1 = 4 A I2 = 6 A
∆W = 10–2 Дж
L = ?
Решение
Энергия магнитного поля внутри соле-ноида с индуктивностью L определяется по формуле:
LI2 LI2 1 2 2 2
По условию задачи
откуда
∆W =W2 −W = L ( 2 − I1 ),
L = 2×∆I1 =10−3 Гн.
42
ЗАДАЧА 13. Однослойная катушка диаметром D = 5 см помещена в однородное магнитное поле, па-
раллельное ее оси. Индукция поля равномерно изменяется со скоростью ∆t =10−2 Тл/с. Катушка содер-жит n = 1 000 витков медной проволоки r =1,75×10−8Ом×м сечением S0 = 0,2 мм2.
1. К концам катушки подключен конденсатор емкостью 10 мкФ. Определить заряд на нем.
2. Концы катушки замкнуты накоротко. Определить тепловую мощность, выделяющуюся в катушке.
∆
B
( )
∆
t
∆
∆
t
t
4
∆
4
t
2
R
∆
4
t
S
3
nS
D
÷
ç
∆
t
ø
è
Дано: ∆B =10−2 Тл/с
S0 =0,2×10−6 м2
Решение
Заряд конденсатора q =C×ei, но
ei = ∆Ф ×n = ∆BS ×n,
r=1,75×10−8 Ом×м
D = 0,05 м С =10−5 Ф
n =1000
где S – площадь сечения катушки, рав-ная pD2 .
q =C ∆B × pD2 ×n =1,95×10−7 Кл.
q = ? Р = ?
Тепловая мощность Р, выделяемая в катушке, равна P = ei .
Здесь ei = ∆B × pD2 ×n, а R = r l ×n. Следовательно 0
P =æ ∆Bö2 × p 16r 0 = 2,8×10−5 Вт.
43