4. Абстрактный тип данных «Дерево»

Операторы, выполняемые над деревьями

1. PARENT(n, Т)- возвращает родителя (parent) узла n в дереве Т.

2. LEFTMOST_CHILD(n, Т). - возвращает самого левого сына узла n в дереве Т.

3. RIGHT_SIBLING(n, Т). - возвращает правого брата узла n в дереве Т и значение L, 4. LABEL(n, Т). - Возвращает метку узла n дерева Т.

5. CREATEi(v, Т1, Т2, ..., Тi) - создает новый корень r с меткой v и далее для этого корня создает i сыновей, которые становятся корнями поддеревьев Т1, Т2, ..., Тi.

6. ROOT(T). - Возвращает узел, являющимся корнем дерева Т. 7. MAKENULL(Т). - делает дерево Т пустым деревом.

Представление деревьев с помощью массивов

• Пусть Т - дерево с узлами 1, 2, ..., n.

• Самым простым представлением дерева Т, поддерживающим оператор PARENT (Родитель), будет линейный массив А, где каждый элемент А[i] является указателем или курсором на родителя узла i.

• Корень дерева Т отличается от других узлов тем, что имеет нулевой указатель или указатель на самого себя как на родителя.

• А[i]=j, если узел j является родителем узла i, и А[i]=0, если узел i является корнем.

Дерево и курсоры на родителей:

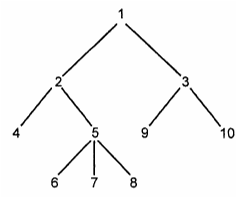
Представление деревьев с помощью списков сыновей состоит в формировании для каждого узла списка его сыновей.

• На рис. показано, как таким способом представить следующее дерево:

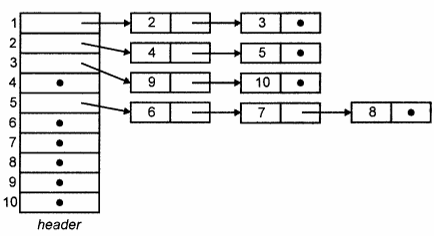
• Здесь есть массив ячеек заголовков, индексированный номерами (они же имена) узлов. Каждый заголовок (header) указывает на связанный список, состоящий из "элементов"-узлов. Элементы списка header[i] являются сыновьями узла i, например узлы 9 и 10 - сыновья узла 3.

5. Абстрактный тип данных «Множество». Методы реализации Мн-ств

Множеством называется некая совокупность элементов, каждый элемент множества или сам является множеством, или является примитивным элементом, называемым атомом. В любом множестве нет двух копий одного и того же элемента. Линейно упорядоченное множество S удовлетворяет следующим двум условиям:

1. Для любых элементов а и b из множества S может быть справедливым только одно из следующих утверждений: а<b, а=b или b<а.

2. Для любых элементов а, b и с из множества S таких, что а<b и b<c, следует а<с (свойство транзитивности).

. Объединением двух множеств является третье множество, содержащее элементы обоих множеств (AÈB). Пересечением двух множеств является третье множество, которое содержит элементы, входящие одновременно в оба множества(AÇB).

Разностью двух множеств является третье множество, которое содержит элементы первого множества, не входящие во второе множество (A \ B).

Операторы АТД, основанные на множествах

1. Процедуры UNTON(A, В, С) имеет "входными" аргументами множества А и В, а в качестве результата - "выходное" множество С, равное AÈB.

2. Процедуры INTERSECTION(A, В, С) имеет "входными" аргументами множества А и В, а в качестве результата - "выходное" множество С, равное A ÇB.

3. Процедуры DIFFERENCES(A, В, С) имеет "входными" аргументами множества А и В, а в качестве результата - "выходное" множество С, равное A\B.

4. Процедура MERGE(A, В, С)- слияние, присваивает множеству С значение AÈB, но результат будет не определен, если A ÇBƹ, т.е. в случае, когда множества А и В имеют общие элементы.

5. Функция MEMBER(x, А) имеет аргументами множество А и объект х того же типа, что и элементы множества А, и возвращает булево значение true (истина), если xÎА, и значение false (ложь), если хÏА.

6. Процедура MAKENULL(A) присваивает множеству А значение пустого множества.

7. Процедура INSERT(x, А), где объект х имеет тот же тип данных, что и элементы множества А, делает х элементом множества А. Другими словами, новым значением множества А будет АÈ{х}.

8. Процедура DELETE(x, A) удаляет элемент х из множества А,

9. Процедура ASSIGN(A, В), присваивает множеству А в качестве значения множество В.

10. Функция MIN(A) возвращает наименьший элемент множества А

11. Функция EQUAL(A, В) возвращает true когда множества А и В состоят из одних и тех же элементов.

12. Функция FIND(x) возвращает имя множества, в котором есть элемент х.

Реализация множеств посредством двоичных векторов

В этой реализации множество представляется двоичным вектором, в котором i-й бит равен 1 (или true), если i является элементом множества.

Главное преимущество этой реализации состоит в том, что здесь операторы MEMBER, INSERT и DELETE можно выполнить за фиксированное С помощью объявлений языка Pascal АТД SET можно определить следующим образом:

const N = { подходящее числовое значение };

type SET = array[1..N] of boolean;

Реализация множеств посредством связанных списков

В данном представлении занимаемое множеством пространство пропорционально размеру представляемого множества, а не размеру универсального множества.

Если универсальное множество линейно упорядочено, то в этом случае множество можно представить в виде сортированного списка, т.е, можно ожидать, что эти элементы в списке будут находиться в порядке е1, е2, e3, ..., еn, когда е<е2<e3<...<еn.

Преимущество отсортированного списка заключается в том, что для нахождения конкретного элемента в списке нет необходимости просматривать весь список.

Элемент будет принадлежать пересечению списков L1 и L2 тогда и только тогда, когда он содержится в обоих списках.

В случае несортированных списков мы должны сравнить каждый элемент списка L1 с каждым элементом списка L2, т.е. сделать порядка О(n2) операций при работе со списками длины n.