
Вступление к Спецкурсу «12 шагов к успеху».
Никто не добивается успеха случайно. Успех требует составления особого плана, которому обязательно нужно следовать. На первый взгляд, это просто, но эта затея требует усидчивости; добиться успеха несложно, но для этого придется немало потрудиться. Благо, стоит только начать, как результаты немедленно дадут о себе знать. Вся прелесть успешной жизни заключается в том, что, сделав один маленький шаг по направлению к успеху, Вы обязательно его добьетесь!
Шаг 1 . Посмотрите в ближайшее зеркало. Человек, который пристально на Вас оттуда смотрит - это единственный человек, который несет ответственность за Ваш успех. Улыбнитесь! В случае неудачи обвинять можно будет только его и никого другого. Успешные люди несут полную ответственность за свои действия.
Тема шага 1: «Сложение и вычитание натуральных чисел. Круги Эйлера»
Задачи 1 и 2 предназначены для закрепления понимания взаимосвязи операций сложения и вычитания. Здесь можно продемонстрировать учащимся способ решения задач «с конца». Для задачи 1 (1) можно сделать такой рисунок.
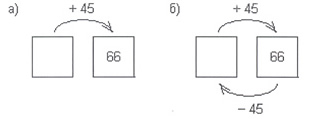
К неизвестному числу прибавили 45 и получили 66 (рис. а), следовательно, для нахождения первого числа надо из 66 вычесть 45 (рис б).
1. 1) Задумали число, увеличили его на 45 и получили 66. Каким действием можно найти задуманное число? Найдите его.
2) Задумали число, уменьшили его на 45 и получили 66. Найдите задуманное число.
3) Задумали число, увеличили его на 120, результат уменьшили на 49. Получили 200. Найдите задуманное число.
2. 1) В автобусе было 25 пассажиров. На первой остановке вышло 8 и вошло 12 пассажиров, на второй — вышло 7 и вошло 5 пассажиров. Сколько пассажиров стало в автобусе после второй остановки?
2) В автобусе было несколько пассажиров. На первой остановке вышло 7 и вошло 4, а на второй вышло 6 и вошло 13 пассажиров. Сколько пассажиров было в автобусе до первой остановки, если после второй остановки автобуса их стало 38?
Условия задач 3–5 заданы в так называемой «косвенной» форме. Здесь для нахождения неизвестного числа требуется определить, оно больше или меньше известного. Эти задачи требуют большего внимания к анализу условия задачи, к выяснению взаимосвязи между известными и неизвестными величинами.
3. В трех классах 44 девочки — это на 8 меньше, чем мальчиков. Сколько мальчиков в трех классах?
4. 1) Сын на 24 года моложе мамы, а папа на 3 года старше мамы. Сколько лет папе, если сыну 10 лет?
2) Мама на 23 года старше сына, а папа на 2 года старше мамы. Сколько лет сыну, если папе 34 года?
5. 1) Алеша прыгнул в длину на 3 м 12 см. Это на 9 см лучше результата Бори и на 13 см хуже результата Вовы. Какой результат в прыжках в длину показал Боря? Какой Вова?
2) Доярки надоили за июль 300 000 л молока, это на 4 000 л больше, чем в июне и на 6 000 л меньше, чем в августе. Сколько литров молока они надоили за летние месяцы?
В задачах 6–7: предложить несколько способов решения, будем это всячески поощрять, так как обсуждение различных способов решения одной и той же задачи, кроме прочего, способствует развитию речи школьников. Для анализа условия и выбора плана решения задачи 6 полезно использовать «круги Эйлера». Завершим работу с такими задачами следующим заданием:
— Миша и Коля за лето прочитали 15 книг. Из них Миша прочитал 10 книг, а Коля — 12. Поставьте различные вопросы и ответьте на них.
По ходу решения получаемые ответы удобно отмечать на рисунке. Например:
1) Сколько книг прочитал Миша, но не прочитал Коля?
15 – 12 = 3 (книг);
2) Сколько книг прочитали оба мальчика?
10 – 3 = 7 (книг); 3) ...

6.*(Часть задач разбирается на шаге 1,
часть – домашнее задание №1)
1) В нашем классе коллекционируют только марки и монеты. Марки коллекционируют 8 человек, монеты — 5, а всего коллекционеров 11. Объясните, как это может быть. Сколько человек коллекционируют только марки? Сколько — только монеты?
2) Из 38 учащихся класса 24 занимаются в хоре и 15 в лыжной секции. Сколько учащихся занимается и в хоре, и в лыжной секции, если в классе нет учащихся, не посещающих занятий хора или лыжной секции?
3) 12 человек участвовали в конкурсе певцов, 3 человека — и в конкурсе певцов, и в конкурсе чтецов. Хотя бы в одном из этих конкурсов участвовали 26 человек. Сколько человек участвовало в конкурсе чтецов?
4) В соревнованиях по прыжкам в длину участвовало 18 человек, а по прыжкам в высоту — 21. Причем и в тех, и других соревнованиях участвовали 16 человек. Сколько человек участвовало в соревнованиях?
5) В нашем классе 30 учащихся. На экскурсию в музей ходили 23 человека, в кино — 21, а 5 человек не ходили ни на экскурсию, ни в кино. Сколько человек ходили и на экскурсию, и в кино?
6) В нашем классе 8 человек коллекционируют марки, 6 человек коллекционируют монеты, причем и марки, и монеты коллекционируют 3 человека, а ничего не коллекционируют 19 человек. Сколько учащихся в нашем классе?
7) В нашем классе 32 человека. Из них 23 — любят кошек, 18 — собак. Причем 10 человек любят и кошек, и собак. Сколько человек из нашего класса не любят ни кошек, ни собак?
8) В нашем классе 30 учащихся. На экскурсию в музей ходили 23 человека, в кино и в музей — 6, а 2 человека не ходили ни в кино, ни на экскурсию. Сколько учащихся из нашего класса ходило в кино?
7. а) Гости спросили: сколько лет исполнилось каждой из трех сестер? Вера ответила, что ей и Наде вместе 28 лет, Наде и Любе вместе 23 года, а всем троим 38 лет. Сколько лет каждой из сестер?
б) На XXII Олимпийских Играх в Москве (1980 г.) спортсмены СССР получили 195 медалей, из них 126 золотых и бронзовых, 149 золотых и серебряных. Сколько золотых, серебряных и бронзовых медалей в отдельности получили спортсмены СССР?
Один из способов решения задачи 7 (а) может быть таким. Обозначим количество лет Веры, Нади и Любы соответственно В, Н и Л. Тогда по условию задачи верны 3 равенства:
В + Н + Л = 38,
В + Н = 28,
Н + Л = 23.
Вычитая из первого равенства второе, а потом третье, получим, что Л = 10, В = 15. Теперь легко вычислить возраст Нади:
Н = 38 – 10 – 15 = 13.
Итак, Вере 15 лет, Наде 13 лет, Любе 10 лет.
II. Круги Эйлера – задачи на пересечение или объединение множеств, Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи. Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.
