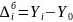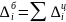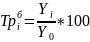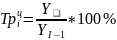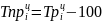- •Билет №1Статистика: понятие, ее предмет и метод. Организация статистики в России.
- •Билет № 3.Статистическое наблюдение: понятие, программно-методологические и организационные вопросы.
- •Билет №4 Организационные формы и способы статистического наблюдения.
- •Билет №5 Виды статистического наблюдения.
- •По охвату единиц совокупности:
- •2) По времени:
- •Билет №6 Статистическая сводка и группировка: назначение, понятие, виды.
- •Билет № 7 Основные этапы проведения группировок.
- •Билет№12 .Средние величины: понятие, классы. Степенные средние величины.
- •Билет№13.Структурные средние величины.
- •2.Дисперсионный метод
- •3.Кореляционно-регрессионный метод
2.Дисперсионный метод
3.Кореляционно-регрессионный метод
4.Графический метод.
Билет№18,17.Непараметрические методы оценки взаимосвязей.Методы корреляционного и дисперсионного анализа не универсальны: их можно применять, если все изучаемые признаки являются количественными. При использовании этих методов нельзя обойтись без вычисления основных параметров распределения (средних величин, дисперсий), поэтому они получили название параметрических методов.Между тем в статистической практике приходится сталкиваться с задачами измерения связи между качественными признаками, к которым параметрические методы анализа в их обычном виде неприменимы. Статистической наукой разработаны методы, с помощью которых можно измерить связь между явлениями, не используя при этом количественные значения признака, а значит, и параметры распределения. Такие методы получили название непараметрических.Если изучается взаимосвязь двух качественных признаков, то используют комбинационное распределение единиц совокупности в форме так называемых таблиц взаимной сопряженности.Однако важно получить обобщающий показатель, характеризующий тесноту связи между признаками и позволяющий сравнить проявление связи в разных совокупностях. Для этой цели исчисляют, например,коэффициенты взаимной сопряженности Пирсона (С) и Чупрова (К):
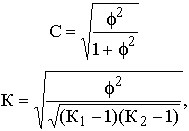
где f2 – показатель средней квадратической сопряженности, определяемый путем вычитания единицы из суммы отношений квадратов частот каждой клетки корреляционной таблицы к произведению частот соответствующего столбца и строки:
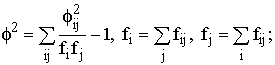
К1 и К2 – число групп по каждому из признаков. Величина коэффициента взаимной сопряженности, отражающая тесноту связи между качественными признаками, колеблется в обычных для этих показателей пределах от 0 до 1.В социально-экономических исследованиях нередко встречаются ситуации, когда признак не выражается количественно, однако единицы совокупности можно упорядочить. Такое упорядочение единиц совокупности по значению признака называется ранжированием. Примерами могут быть ранжирование студентов (учеников) по способностям, любой совокупности людей по уровню образования, профессии, по способности к творчеству и т.д.При ранжировании каждой единице совокупности присваивается ранг, т.е. порядковый номер. При совпадении значения признака у различных единиц им присваивается объединенный средний порядковый номер. Измерение связи между ранжированными признаками производится с помощью ранговых коэффициентов корреляции Спирмена (r) и Кендэлла (t). Эти методы применимы не только для качественных, но и для количественных показателей, особенно при малом объеме совокупности, так как непараметрические методы ранговой корреляции не связаны ни с какими ограничениями относительно характера распределения признака.
Билет№19.Показатели ранговой корреляции.
Вычисление ранговой корреляции помогает определить силу и направление корреляционной связи между двумя признаками, измеренными в ранговой шкале. Коэффициент ранговой корреляции Кендалла
Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:
![]() ,
,
где ![]() .
.
![]() —
суммарное
число наблюдений, следующих за текущими
наблюдениями с большим значением
рангов Y.
—
суммарное
число наблюдений, следующих за текущими
наблюдениями с большим значением
рангов Y.
![]() —
суммарное
число наблюдений, следующих за текущими
наблюдениями с меньшим значением
рангов Y. (равные
ранги не учитываются!)
—
суммарное
число наблюдений, следующих за текущими
наблюдениями с меньшим значением
рангов Y. (равные
ранги не учитываются!)
![]()
Если исследуемые данные повторяются (имеют одинаковые ранги), то в расчетах используется скорректированный коэффициент корреляции Кендалла:
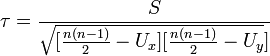
![]()
![]()
![]() —
число
связанных рангов в ряду X и Y соответственно.
—
число
связанных рангов в ряду X и Y соответственно.
Коэффициент ранговой корреляции Спирмена
Каждому
показателю X и Y присваивается ранг. На
основе полученных рангов рассчитываются
их разности ![]() и
вычисляется коэффициент корреляции
Спирмена:
и
вычисляется коэффициент корреляции
Спирмена:
![]()
Коэффициент корреляции знаков Фехнера
Подсчитывается количество совпадений и несовпадений знаков отклонений значений показателей от их среднего значения.
![]()
C — число пар, у которых знаки отклонений значений от их средних совпадают.
H — число пар, у которых знаки отклонений значений от их средних не совпадают.
Билет№20.Ряды динамики: понятие, виды, правила построения.
Ряд динамики – это система показателей характеризующих изменение явления во времени. Любой ряд динамики состоит как минимум из двух показателей:
1.Время (t)
2.У= уровень показателя
Задачи статистического изучения явлений во времени:
1.Характеристика интенсивности изменения во времени статистических показателей.
2.Определение средних показателей во времени.
3.Выявление средних закономерностей во времени.
4.Экстраполяция, интерполяция.
5.Анализ фактов, определяющих изменение показателей во времени.
Классификация рядов динамики:
1.Время(моментные – в том случае когда время это момент времени, конкретная дата, интервальные – интервальный ряд будет в том случае когда у-есть результат развития явления во времени(ВВП)) ; Суммирование уровней динамики не имеет экономического смысла, суммирование уровней интервального ряда позволяет получить новый показатель.
1.Полнота охвата во времени: - полные(расстояние между датами или интервалами времени одинаковое или его нет вообще), - неполные(в противном случае) –
2.Форма представления уровня ряда: - абсолютный, - относительный, - средних величин.
Правила построения рядов динамики:
периодизация(типологическая группировка явлений во времени )
сопоставимость(цены, територии, методики расчета.)
соответствие интенсивности изменений во времени.
Билет№21.Показатели анализа рядов динамики.
Показатели рядов динамики делятся на две группы: цепные и базисные.
Цепные: в том случае когда сравнение производится с предыдущим уровнем ряда динамики.
Базисные – в том случае когда сравнение производится с уровнем взятм за базу сравнения (одним и тем же) чаще всего этим уровнем являеся начальный уровен ряда динамики:
Показатель |
Базисный |
Цепной |
Взаимосвязь |
Абсолютный прирост |
|
|
|
Темп роста |
|
|
Трiб=ПТрiц |
Темп прироста |
|
|
Проявляется через Тр |
Абсолютное содержание 1% прироста |
Обычно не стичается |
A%= |
-------------------- |
Темп
прироста =

Билет№22.Средние показатели ряда динамики.
Средний
абсолютный прирост:
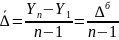 =
=
Средний
темп роста: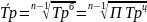
Средний
темп прироста: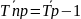
n – число уровней ряда динамики,
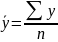 -
если ряд динамики интервальный, то
средний уровень находится по средней
арифметической простой.
-
если ряд динамики интервальный, то
средний уровень находится по средней
арифметической простой.
Если ряд динамики моментальный полный, используем среднюю хронологическую простую:
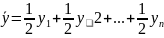
Если ряд динамики моментный неполный, то используем среднюю хронологическую взвешенную.
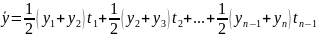
Билет№23.Проверка ряда динамики на наличие тренда. Выявление тенденций развития в рядах динамики: метод укрупнения интервалов, метод скользящей средней.
1)тренд
2)циклические и переодические колебания
3)сезонные колебания
4)случайные колебания
Изучение тренда:
1эт:проверка ряда динамики на наличие тренда если есть
2эт:выравнивание измерения
3эт:экстрополяция полученных результатов
Методы:
1)Укрепление интервалов
Уровни по годам, то растут, то падают, и не позволяют увидеть тенденцию чтобы выявить: переход к расчету уровня за большие промежутки времени. если ряду динамики 10 лет, то ряд динамики не применим
2)Скользящей средней
Для каждого уровня ряда определяется средний из близ лежащих. Испол-ют трех звенную ,5 звенную
Yi=Yi-1+Yi+Yi+1-трех звенная
3
Yi=yi-2+yi-1+yi+yi+1+yi+2-5 звенная
Билет№24.Выявление тенденций развития в рядах динамики: метод аналитического выравнивания.
Считается наиболее эффективным методом,т.к он позволяет экстрополяцию и интерполяцию
Идея: заключается в предоставление уровня ряда динамики в виде функции от времени
Уровнение трендов: yt=a0+a1t
Подбор функции осуществляется, так же как при построении уравнений регрессии.
Находим параметры уравнения (метод наименьших квадратов, наименьших расстояний, метод избранных точек)
Na+bEx=Ey
aEx+bEx2 =Exy
a=EyEx2-ExExy b=nExy-EyEx
nEx2-(Ex)2 nEx2-(Ex)2
Для упрощения расчета t заменяют чтобы сумма Et=0,и тогда
A0=Ey a1=Eyt
N Et2
A0-ср. уровень ряда
А1-сила связи, покажет на сколько изменится результат при изменении времени на единицу
Имея уровень тренда мы можем прогназировать явление на вр вперед
Билет№25.Изучение сезонных колебаний в рядах динамики.
Колебание уровней рядов динамики причиной является процессы связанные со сменой времени года.
Уровень сезонности определяется при помощи: индекс сезонности методика расчета зависит от наличия тренда в ряду динамики.
Если тренда нет то технология расчета такая:
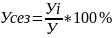
Уi-сезонное значене
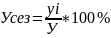
Уi=Уi1+Уi2+Уi3+Уi4+…+Уin
N
Если тренд есть, то индекс значение это выравнивание значение
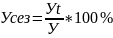
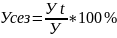
Уt=Уt1+Уt2+….+Уtn
N
Билет№26.Индексы: понятие, решаемые задачи, единицы измерения, виды.
Индекс-сравнение двух состоянии одного явления
Формы:
1)отношение двух велечин
2)разность
Задачи решаемые с помощью индексов
1)определение обобщающего показателя
2)изучение динамики средних велечин
3)изучение факторов в динамики сложных явлении
Билет№27.Агрегатный индекс как основная форма общих индексов.
Общие (сводные) индексы показывают соотношение совокупности явлений, состоящих из разнородных, непосредственно несоизмеримых элементов. Только в этом случае становится возможным сравнение, следовательно и исчисление индексов. В общих индексах различают индексируемые величины и веса. Тот показатель, изменение которого характеризует индекс, называется индексируемой величиной. Показатель, применяемый в качестве постоянного, называется весом (соизмерителем). Агрегатный индекс – основная форма общих индексов. Основной формой общих индексов является агрегатная форма. Агрегатным индексом называется соотношение сумм показателей, отражающих порядок расчета общих индексов непосредственно по данным об индексируемых величинах и их весах.
Билет№28.Общие индексы как средние из индивидуальных индексов.
P1-цена отчетного периода
P0-цена базисного периода
Q1-количество отчетного периода
Q0-количество базисного периода
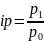 ip=
ip=
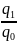 ipq=
ipq=
p1-p0 q1-q0 p1q1-p0q0
ip*iq=ipq
Общие индексы:
Ip=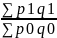 Iq=
Iq=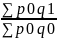 Ipq=
Ipq=Ip*Iq
Ipq=
Ipq=Ip*Iq
Билет№29.Индексы средних величин: индексы переменного, постоянного составов, структурных сдвигов.
Гармонические индекс
Ip=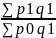 ip=
ip=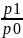 =p0=
=p0=
Cредне арефметическая
Iq=
iq=
Индексы средних велечин:
Iпер=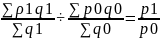
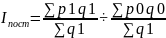
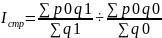
Билет№30.Территориальные индексы: понятие, способы расчета.
Территориальные индексы представляют собой разновидность относительных величин сравнения, когда сопоставляются сложные показатели, относящиеся к одному и тому же периоду времени, но к разным территориям (городам, районам, областям, государствам). На основе территориальных индексов выполняются международные сопоставления.
Территориальный индекс товарооборота — это отношение суммы выручки от продажи в одном из районов к аналогичному показателю в другом. Один из районов (например, Б) берется за базу сравнения т.е.

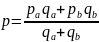

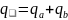
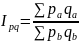
Ipq≠Ip*Iq