Билет№12 .Средние величины: понятие, классы. Степенные средние величины.

Средняя величина - это типическая характеристика совокупности.

Правила счета средних величин: 1. Необходимо исходить из качества содержания осредняемого признака. 2. Средняя должна рассчитываться по одной совокупности. 3.Общие средние должны подкрепляться груповыми.4. необходим обоснованный выбор единицы совокупности, для которой рассчитывается средняя.

Виды средних величин:

1.Степенные (средняя арифметическая, средняя гармоническая)

2.Структурные(мода, медиана, квартили и децили ).

Виды степенных средних величин:

Вид степенной средней величины зависит от показателя m и от формы представления данных. Если данные имеют не сгруппированный вид то используется простая формула расчета, если сгруппированный то взвешенная. Взвешенная формула применяется толь тогда когда есть группировка. Арифметическая и гармоническая это две противоположные формулы. Если в логической формуле расчета неизвестен числитель считается средняя арифметическая, если неизвестен знаменатель то рассчитывается средняя гармоническая.

Средняя геометрическая определяется для расчета средних показателей анализа рядов динамики.

Средняя квадратическая используется для расчета показателей вариации.

Билет№13.Структурные средние величины.

Мода – варианта (х), чаще всего встречается в совокупности т.е. варианта с наибольшей частотой.

Медиана – варианта (х), которая делит упорядоченный ряд на две равные части.

Мода и медиана в дискретном ряду распределения находятся визуально. В интервальном ряду распределения мода и медиана находятся при помощи формул

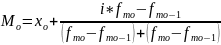
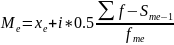
Билет №14.Вариация признака: понятие, необходимость статистического изучения. Показатели вариации.

Вариация – это наличие различий значений признака у отдельных единиц совокупности.

Показатели вариации оценивают: 1.Калеблемость значений признака у единиц совокупности. 2. Устойчивость развития изучаемых процессов во времени. 3. Влияние факторного признака на изменение результативного признака. 4. Различного рода риски.

Основные показатели вариации:

1.Размах вариации (R) R=x_max – x_min

А.Недостатки показателя:

Сильно зависит от максимальных аномальных значений признака.

1.Не учитывает внутреннее вариацию между границами, определяемыми максимальным и минимальным значением. Среднее линейное отклонение (или среднее абсолютное отклонение) (d – показывает абсолютный размер отклонения в среднем от индивидуальной величины) 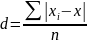; - простая формула расчета – взвешенная формула расчета.

1.Дисперсия и среднее квадратическое отклонение. Дисперсия показывает средний квадрат отклонений индивидуальных значений признака от средней величины.

2.Коэффициент вариации (V) Особенности: 1.Относительная величина 2. Если его величина меньше 33% то совокупность по данному признаку является однородной 3. Может приводить к выводам, противоположным результатам полученным на основе абсолютных показателей вариации.

При проведении группировки совокупность делится на группы однородные по какому либо признаку. Это деление приводит к тому, что общая вариация (изменчивость) будет распадаться на две: Факторная вариация (связанная с градациями группировочного признака) Остаточная вариация (вариация отражает изменчивость признака вод влиянием прочих факторов).

Билет№15.Виды дисперсий. Правило сложения дисперсий.

При проведении группировки совокупность делится на группы однородные по какому либо признаку. Это деление приводит к тому, что общая вариация (изменчивость) будет распадаться на две: Факторная вариация (связанная с градациями группировочного признака) Остаточная вариация (вариация отражает изменчивость признака вод влиянием прочих факторов).Таким образом для измерения факторной и остаточной вариаций необходимы показатели. К таким показателям относится дисперсия. Для отражения факторной вариации используется межгрупповая дисперсия, а для измерения остаточной вариации – внутригрупповая дисперсия. В сумме обе дисперсии дадут общую вариацию признака. Для этого существуют правила сложения дисперсий:

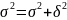
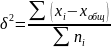
Покажет вариацию признака х связанную с гравировочным признаком.

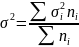
Коэффициент детерминации(эмпирический коэффициент) показывает что это относительная величина структуры. Показывает долю межгрупповой дисперсии в общей дисперсии.

Эмпирическое корреляционное отношение. Если оно колеблется от 0< < 0,3 – связь слабая, 0,3< <0,7 – умеренная, 0,7< <1 – сильная.

Билет№16.Понятие о связи. Задачи статистического изучения взаимосвязей. Виды и формы связей.

Связи бывают – причинные, - связи соответствий.

Необходимость изучения взаимосвязей: структуры взаимодействия)

- практическая (переход от объяснения связей к изменению факторов)

Этапы изучения связей:

1.Установление связей

2.Изменение связей(оценка интенсивности связей)

3.Расчет прогнозных, нормативных оценок показателей на основе проведенного измерения связей.

Классификация связей:

1)Форма проявления : - функциональная – когда конкретному х соответствует конкретное у. – Стохастическая – когда конкретному х соответствует распределение значений у.

2)Направление: - прямое х и у изменяется в одном направлении, - обратное

3) аналитическая форма - линейные – можно провести линию, - нелинейные.

4) Число взаимодействующих факторов : - парная(х влияет на у), -множественная(х1,х2,х3 влияют на у).

5) По степени взаимодействия: - непосредственные (признак сам влияет на результат), - косвенные (признак влияет на результат через уровень признака),

6) По силе: -слабые, -сильные.

Статистические методы изучения связей:

1.Функциональные (если данные представлены функцией у=f(х) балансовый метод, Средние и относительные величины (равенство) )

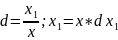2.Индексный метод (стохастические – данные представлены в виде таблиц )

3.Метод параллельных рядов (а)если данные представлены таблицей сопряженности. Показывает меры связи, основанные на х² (хи квадрат) Теоретико-информационные связи. б) Если данные представлены в виде аналитической группировки. )

1.Метод аналитической группировки (показатели силы и тесноты связи а) если данные представлены в виде функции)