Взаимное расположение прямой линии и плоскости

Возможны следующие три случая взаимного расположения прямой и плоскости:

1. прямая принадлежит плоскости;

2. прямая параллельна плоскости;

3. прямая пересекает плоскость.

4. прямая перпендикулярна плоскости

1. Первый случай мы уже рассматривали. Критерием этого случая является следующее свойство плоскости: если прямая линия соединяет две точки данной плоскости, то такая прямая лежит в этой плоскости.

2. Прямая параллельная плоскости.

П ри решении вопроса о параллельности плоскости и прямой линии, необходимо опираться на известное положение стереометрии: прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскости.

Прежде всего проедем через прямую вспомогательную плоскость , например, горизонтально проецирующую. Далее строим проекции n₁ и n₂ линии пересечения плоскостей, сравнения которых с проекций данной прямой показывают, что прямая a не параллельна плоскости ABC.

3. Прямая, пересекающая плоскость.

Это одна из основных задач как начертательной геометрии, так и компьютерной графики. Она состоит из трех этапов.

1. Построение вспомогательной плоскости , которую проводят через прямую a.

2. Построения линии пересечения n вспомогательной плоскости  и заданной .

3. Определение искомой точки как точки пересечения двух прямых: данной a и построенной n (K=an)

В качестве вспомогательной плоскости  рекомендуется брать одну из проецирующих.

На рисунке D - точка пересечения ABC и прямой a.

4. Прямая, перпендикулярная плосоксти.

Из стереометрии: прямая перпендикулярна плоскости, если она перпендикулярна двум прямым этой плоскости.

Докажем следующую теорему о перпендикуляре и плоскости: если прямая перпендикулярна плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция – фронтальной проекции фронтали той же плоскости.

, h||₁

, т.к. , то на основании теоремы о проецировании прямого угла можно утверждать, что . Аналогично, проведя через точку B по плоскости  фронталь, можно доказать, что .

Взаимное расположение двух плоскостей

Две плоскости в пространстве либо взаимно параллельны, либо пересекаются. Взаимно перпендикулярные плоскости представляют собой частный случай пересекающихся плоскостей.

1. Параллельные плоскости.

П лоскости параллельны, если две пересекающихся прямые одной плоскости, соответственно параллельны двум пересекающимся прямым другой плоскости.

Через данную точку A провести плоскость  параллельную данной плоскости  (ab).

2. Пересекающиеся плоскости

Линией пересечения двух плоскостей является прямая, для построения которой достаточно определить две точки, общие обеим плоскостям. Пред тем как рассмотреть построение линии пересечения двух плоскостей разберем вспомогательную задачу: найдем току пересечения прямой общего положения с проецирующей плоскостью

Д ана прямая a и горизонтальная проецирующая плоскость , тогда горизонтальная проекция K₁ искомой точки должна одновременно лежать на горизонтальной проекции ₁ плоскости  и на горизонтальной проекции a₁ прямой a, т.е. в точке пересечения a₁ с ₁: K₁=a₁₁. Фронтальная проекция K₂ точки K расположена на линии проекционной связи и на фронтальной проекции a₂ прямой a. (На рисунке не приведена проекция ₁, т.к. в данном случае она нас не интересует и может быть произвольной.)

Теперь разберем один из частных случаев пересечения плоскостей, когда одна из них проецирующая.

Н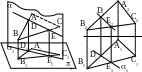 айдем две общие точки для этих двух плоскостей. Очевидно, этими общими точками для ABC будут точки пересечения сторон AB и BC с проецирующей плоскостью . Построение таких точек D и E как на пространственном чертеже, так и на эпюре базируется на предыдущем рассмотренном примере.

Таким образом, горизонтальная проекция D₁E₁ линии пересечения заданных плоскостей совпадает с горизонтальной проекцией плоскости .

Рассмотрим теперь общий случай. Пусть в пространстве заданы две плоскости общего положения  и . Для определения двух искомых точек заданные плоскости пересекают двумя вспомогательными проецирующими плоскостями. В качестве таких плоскостей целесообразно взять плоскости уровня.

Т .к. => , где

Т.к. => , где

Отрезок [AB]=.