Различные положение плоскости относительно плоскостей проекций

Различают плоскости общего положения, перпендикулярные плоскостям проекций и плоскости уровня.

Плоскость перпендикулярная ₁ называется горизонтальной проецирующей плоскостью. Горизонтальная проекция такой плоскости вырождается в прямую. Углы  и , которые образуются между плоскостью ( и ₂) и (и ₃) соответственно, проецируются на ₁ без искажения.

Плоскость  перпендикулярная ₂ называется фронтальной проецирующей плоскостью. Углы между ( и ₁) и ( и ₃) проецируются на ₂ без искажений.

Плоскость  перпендикулярная ₃ называется профильной проецирующей плоскостью. Углы между ( и ₁) и ( и ₂) проецируются на ₃ без искажений.

Плоскость параллельная _называется горизонтальной плоскостью уровня. Она перпендикулярна ₂ и ₃. Любая фигура, расположенная в плоскости  проецируется на горизонтальную плоскость проекций ₁ без искажений. Плоскости, параллельные ₂ и ₃ называются, соответственно, фронтальной и профильной плоскостями уровня.

Прямые линии и точки, расположенные в данной плоскости

Рассмотрим две основные задачи, на взаимную принадлежность точки, прямой и плоскости.

Задача 1. Построить проекции произвольной прямой l, принадлежащей плоскости общего положения , заданной двумя пересекающимися прямыми m и n.

В оспользуемся основной аксиомой принадлежности, утверждающей, что прямая принадлежит плоскости, если две точки этой прямой принадлежат той же плоскости.

Am, Bn

Al, Bl

Задача 2. Построить проекции точки A, которая принадлежит плоскости общего положения , заданной параллельными прямыми m и n.

Е сли точка расположена в плоскости, то из трех координат, определяющих ее положение в пространстве, произвольно можно задавать только две. Эти любые две координаты позволяют построить только одну проекцию точки. Возникает вопрос, как найти вторую (и, автоматически, и третью) ее проекции. Для этого воспользуемся другой аксиомой: если точка принадлежит плоскости, то она принадлежит любой прямой этой плоскости, проходящей через данную точку.

Пусть известна проекция A₂, чтобы найти проекцию A₁ нужно провести вспомогательную прямую через A₂, найти точки пересечения этой прямой с прямыми m₂ (точка B₂) и n₂ (точка C₂). Затем нужно достроить проекции этих точек, построить прямую через B₁C₁, и достроить проекцию A₁.

Главные линии плоскости

С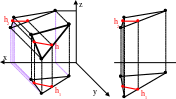 реди прямых линий, которые могут быть расположены в данной плоскости, особое место занимают четыре вида линий, называемых главными линиями плоскости:

1. горизонтали – прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций ₁. Фронтальная и профильная проекции горизонтали горизонтальны. (На рисунке показаны горизонтальная и фронтальная проекции);

2. фронтали – прямые, расположенные в данной плоскости и параллельные фронтальной плоскости проекций ₂.

3. профильные прямые – прямые, расположенные в данной плоскости и параллельные профильной плоскости проекций ₃.

4. линии наибольшего ската – прямые, проведенные по плоскости перпендикулярно к горизонталям

На любой плоскости можно провести бесконечной множество главных линий. Все линии четырех видов образуют плоские пучки параллельных прямых (например, все горизонтали параллельны между собой).

Н е трудно показать, что горизонтальная проекция линии наибольшего ската перпендикулярна горизонтальной проекции горизонтали плоскости. Действительно, если, по определению линии наибольшего ската, угол ABC – прямой, а сторона h этого угла параллельна ₁ (т.е. является горизонталью), то этот прямой угол должен проецироваться на плоскость ₁ без искажений (согласно теореме о проекции прямого угла), т.е. h₁ перпендикулярна A₁B₁.

Важно отметить, что линия наибольшего ската и ее горизонтальная проекция образуют угол, которым измеряется двугранный угол, составленный данной плоскостью (fh) и плоскостью проекций ₁ (т.к. плоскость ABB₁A₁ перпендикулярна и плоскости ₁ и плоскости ABC).