Прямая. Задание прямой линии.

Задание прямой линии возможно несколькими следующими способами:

1. двумя точками;

2. двумя проекциями;

3. двумя плоскостями;

4. точкой и углами наклона к плоскостям проекций;

5. точкой и направляющим вектором.

Рассмотрим вариант 2.

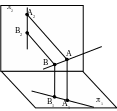
┴₁ (A₁B₁)

┴₂ (A₂B₂)



А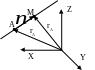 налитические способы задания.

или, если заданы P₁ и P₂

или через координаты

Различные положения прямой линии относительно плоскостей проекций

П рямой общего положения называется прямая, не параллельная ни одной из плоскостей проекций.

Прямые, параллельные плоскостям проекций, называются прямыми уровня.

Прямые, параллельные горизонтальной плоскости проекции называют гроризонталями или горизонтальными лниями уровня.

Т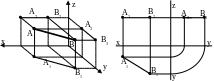 .к. для всез точек горизонтали одинаковое расстояние от плоскости ₁ (XY), то для любой пары точек горизонтали должно выполнятся равенство Z_A=Z_B и, следовательно, на комплексном чертеже фронтальная проекция A₂B₂ будет параллельна оси OX. Горизонтальная проекция может занимать относительно оси любое положение, а профильная - параллельна оси OY.

Прямые, параллельные фронтальной плоскости проекции называют фронталями или фронтальными лниями уровня.

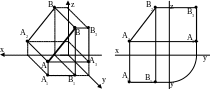
П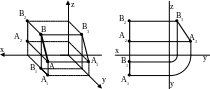 рямые, параллельные профильной плоскости проекции называют профильными лниями уровня.

Прямые, перпендикулярные плоскости проекций, называются проецирующими. В точку обращается проекция прямой на ту плоскость, относительно которой прямая перпендикулярна. Например, для горизонтально проецирующей прямой получим:

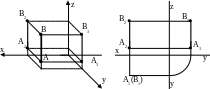
Взаимное расположение точки и прямой

Если точка лежит на прямой, то ее проекции должны лежать на одноименных проекциях этой прямой:

z

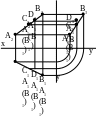
Когда прямая и точка расположены в плоскости параллельной какой-либо из плоскостей _i, то вопрос об их взаимном отношении может быть решен при построении проекций на плоскость _i.

Одним из свойств параллельного проецирования является свойство пропорциональности, т.е. если точка делит отрезок прямой в данном отношении, то проекции этой точки делят одноименные проекции прямой в том же отношении. Таким образом, чтобы на комплексном чертеже разделить отрезок в каком-то отношении, необходимо разделить в соответствующим отношении проекции этого отрезка.

О пределение длины отрезка прямой и угла ее наклона к плоскости проекции

Длину отрезка прямой AB можно определить из прямоугольного треугольника AB’B, в котором:

• катет AB’=A₁B₁ (проекция отрезка AB на плоскость ₁);

• катет BB’=Z – разность расстояний точек A и B от плоскости ₁.

У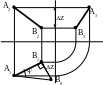 гол  в том же треугольники определяет угол наклона отрезка прямой к плоскости ₁.

Аналогично для ₂ и ₃.

На комплексном чертеже длина отрезка A₁B₀ будет равна длине отрезка AB, а угол  - это угол наклона прямой к плоскости ₁. Точка B₀ получена путем построения отрезка B₁B₀, перпендикулярного A₁B₁ и равного Z.

,

Взаимное расположение двух прямых линий

1. Пересекающиеся прямые. В этом случае прямые a и b имеют одну общую точку К, т.е. пересечения проекций расположены на одной проекционной связи:

z

b₂

K₂

a₂

K

x

b

a

y

a₁

K₁

b₁

2. Параллельные прямые. Из свойства параллельного проецирования – проекции параллельных прямых – параллельны.

3. Скрещивающиеся прямые. Прямые не пересекаются и не параллельны между собой, т.е. проекции пересекаются, но точки пересечения не лежат на одной линии проекционной связи. Точки K и L, а так же E и F называются конкурирующими.

4. Перпендикулярные прямые. Для того, чтобы прямой угол проецировался без искажений, необходимо и достаточно, чтобы, по крайне мере, одна его сторона была параллельна плоскости проекции, а вторая сторона – не перпендикулярна этой плоскости.