Метод проекций Проецирование. Отображение геометрического объекта на плоскости

Машинная графика появилась на основе достижений кибернетики и начертательной геометрии. Начертательная геометрия – это раздел геометрии, в котором пространственные фигуры изучаются с помощью изображения на плоскости. Отображение же геометрической фигуры на плоскость (или на какую-либо другую поверхность) можно осуществить путем проецирования ее точек на эту плоскость (поверхность).

Таким образом, в основу построения любого изображения положена операция проецирования, которая заключается в следующем: имеется плоскость проекций _i (картинная плоскость), на которой хотим получить изображение оригинала – точки A. Операция проецирования заключается в проведении через точку A прямой, которая называется проецирующей. Точка A_i пересечения проецирующей прямой с плоскостью _i называется проекцией точки A на плоскость _i.

Для определения в пространстве проецирующей прямой зададим точку S≠A, через которую проходят все проецирующие прямые. Точка S называется центром проецирования. Операция в этом случае называется центральным проецированием, а ее результат - центральной проекцией. Другой способ определения проецирующей прямой – задание вектора не параллельного _i, называемого направлением проецирования. Проецирующие прямые строят параллельными . Такая операция называется параллельным проецированием. Соответственно, проекция называется параллельной.

В случае параллельного проецирования проецирующие прямые наклонены по отношению к плоскости проекции под углом . Если ≠90º, то проецирование называется косоугольным. Соответственно, и проекция называется косоугольной. Когда =90º, проецирование называется прямоугольным (ортогональным), проекция называется прямоугольной (ортогональной).

Дополнение евклидова пространства.

Рассмотрим следующие примеры центрального проецирования.

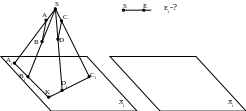
Т.к. , то по смыслу операции должна существовать , но такой точки нет, т.к. (AB)║(CD). Возникает нарушение соответствия, устанавливаемого проецированием между оригиналом и проекцией. Рассмотрим меры по устранению такого несоответствия.

Операцию центрального проецирования мы рассматриваем в евклидовом геометрическом пространстве. В евклидовом пространстве параллельные прямые не пересекаются. Условимся считать параллельные прямые пересекающимися в бесконечно удаленной (несобственной) точке. Каждая прямая дополняется несобственной точкой, к каждая точка дополняется несобственной прямой. Их совокупность порождает несобственную плоскость. Пространство, дополненное несобственными элементами – точками, прямыми и плоскостью – называется расширенным евклидовом пространством. Таким образом, дополнение евклидова пространства приводит к тому, что восстанавливается соответствие между точками оригинала и их проекциями.

В связи с тем, что каждая точка пространства при заданном аппарате проецирование будет иметь одну и только одну проекцию, но обратное утверждение не имеет место. Для определения положение точки в пространстве, необходимо иметь две ее центральные (или параллельные) проекции, полученные при двух различных центрах (или направлениях) проецирования.

Ортогональное проецирование обладает рядом преимуществ перед центральным и параллельным косоугольным проецированием. К ним в первую очередь следует отнести:

1. простоту геометрических построений для определения ортогональных проекций точек;

2. возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры.

Два важных свойства ортогональной проекции:

• проекции взаимно параллельных прямых также взаимно параллельны, а отношение отрезков таки прямых равно отношению их параллельных проекций;

• для того, чтобы прямой угол проецировался ортогонально без искажения, необходимо и достаточно, чтобы, по крайне мере, одна его сторона была параллельна плоскости проекции, а вторая сторона – не перпендикулярна этой плоскости.