13. Электромагниты переменного тока. Сравнительный анализ зависимостей

I, Ф, F_ЭМ = f(δ) электромагнитов переменного и постоянного тока.

В сравнении с ЭМП в ЭМТ при синусоидальном напряжении и отсутствии насыщения магнитной системы ток и поток изменяются по закону синуса. Особенности:

1) В магнитопроводе ЭМТ потери на гистерезис и вихревые токи. В результате магнитное сопротивление стали возрастает, при этом удельное сопротивление стали будет состоять из активной составляющей и реактивной составляющей обусловленной потерями в стали.

– справочнике.

Расчёт цепи ведётся в комплексной форме. Для уменьшения потерь в стали и следовательно магнитную систему шихтуют и выполняют из стали с повышенным удельным сопротивлением.

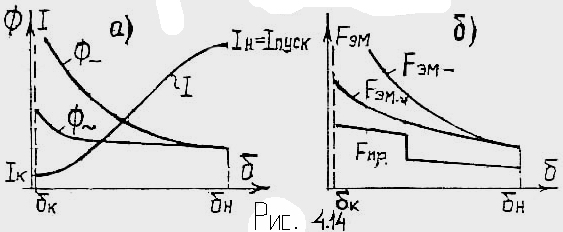
2) (рис.4.14) анализ с помощью закона Ома.

Неполное включение при переменном токе опасно.

При неизменном напряжении сети магнитный поток не зависит от величины зазора, это обеспечивается током катушки.

при изменении воздушного зазора.

3) рис 4.13

В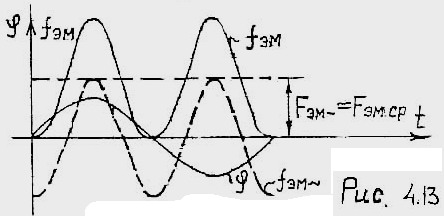 ывод:

• – не меняет своего направления.

• – можно разложить на 2-е составляющие переменную изменяющуюся с двойной частотой относительно частоты сети и постоянную составляющую равную .

.

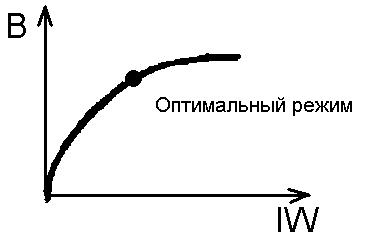
4) Статическая тяговая характеристика и сравнение ЭМП и ЭМТ по .

где – коэффициент рассеивания магнитной системы, который при изменении от до изменяется незначительно. поэтому – изменяется незначительно (пологая).

Т.о. крутизна значительно меньше крутизны ЭМП.

с

с

1)

2)

при притянутом положении якоря

для преодоления одной будет иметь меньшую материалоёмкость ( обмотки) чем электромагнит постоянного тока, это особенно справедливо при больших ходах . При малом ходе предпочтительнее электромагнит постоянного тока.

ЭМТ позволяет иметь большой коэффициент возврата до 0,7, который будет тем больше, чем меньше превышение электромагнитной характеристики над противодействующей характеристикой при . (см. § 4.5) Столь высокий коэффициент возврата позволяет осуществлять защиту двигателей от недопустимого снижения напряжения.

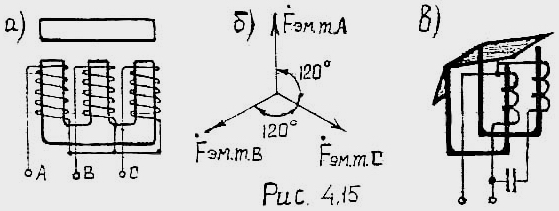
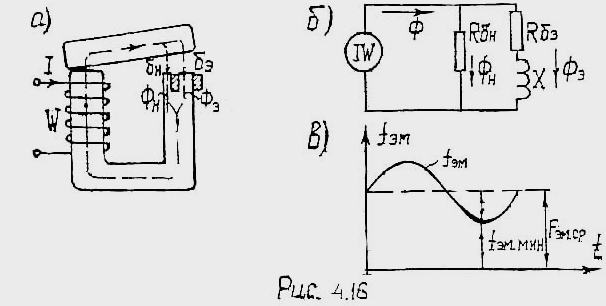
Для уменьшения вибрации рис. 4.16а, 4,15а. Принцип действия к.з.– витка по Л.Р. №2.

и в отличии от не однозначно, т.к. оно зависит от фазы напряжения в момент включения или отключения электромагнита. Если считать цепь электромагнита чисто индуктивной, т.е. ток сдвинут от напряжения на угол 90⁰, то при начальной фазе U,=0 пусковой ток будет содержать апериодическую составляющую.

; ; ; .

Учитывая, что . Это объясняет высокое быстродействие .

14. Нагрев токопровода при коротком замыкании. Расчёт температуры в конце кз.

Процесс нагрева при КЗ подчиняется тем же законам, что и процесс при номинальных режимах работы. Однако здесь есть свои особенности, которые обусловлены:

1) большим значением тока КЗ I_к (I_к/I_дл = 20 - 30 и более), большой мощностью потерь (P_к/P_дл = 400 - 900 и более) и большой скоростью нагрева токопровода [(dθ/dt)_max=P_к/cm];

2) малой длительностью нагрева (при современной релейной защите и отключающих устройствах время КЗ t_к<3 c);

3) сложным характером изменения тока КЗ во времени, обусловленным апериодической составляющей тока и работой автоматической системы регулирования напряжения генератора.

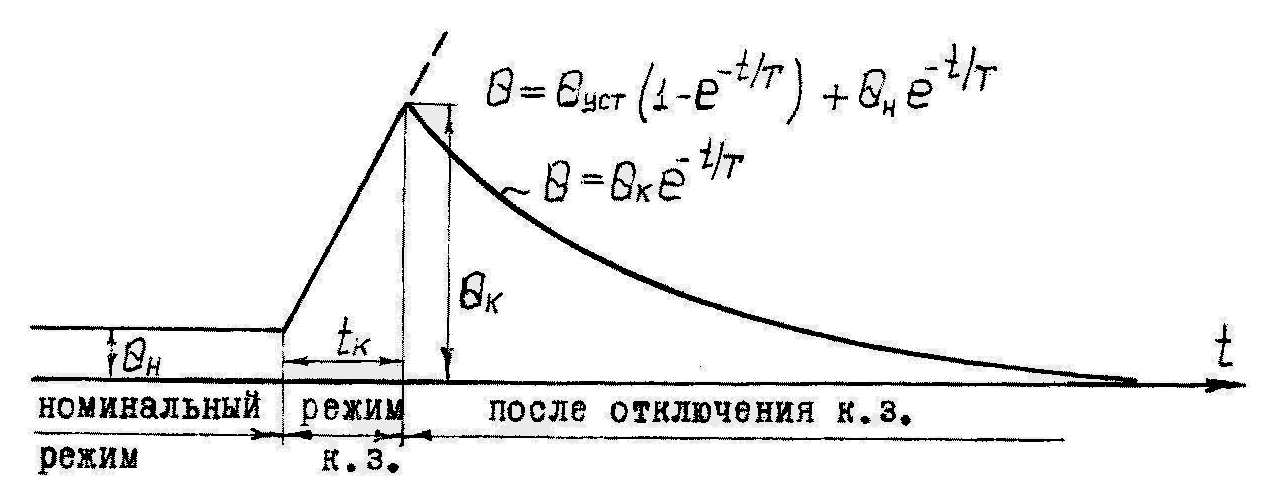
Рис. 2.7. Кривые нагрева и охлаждения токопровода при КЗ

При расчёте нагрева токопровода примем следующие допущения:

1) ввиду незначительности t_к будем считать, что процесс нагрева адиабатический, т. е. без отдачи тепла в окружающую среду. Это допущение даёт погрешность не более 2,5%, если ;

2) ток КЗ не меняется и остаётся равным установившемуся значению тока при КЗ I_к.

При этих допущениях уравнение теплового баланса токопровода при коротком замыкании примет вид . (2.39)

Сделав преобразования и проинтегрировав обе части уравнения (2.39), получим

где γ – плотность материала токопровода.

Так как температура токопровода при КЗ изменяется в большом диапазоне, то при решении данного уравнения необходимо учитывать изменение ρ и С в функции θ:

, (2.40)

где с₀ – удельная теплоёмкость при 0 °С;

β – температурный коэффициент теплоёмкости;

А_к, А_н – значение интеграла при верхнем и нижнем пределах интегрирования.

Интеграл уравнения (2.40) зависит лишь от свойств материала и пределов интегрирования. Поэтому для облегчения расчётов для наиболее распространённых проводниковых материалов построены зависимости , которые получили название кривых адиабатического нагрева.

Полученная формула (2.40) позволяет рассчитать:

1) температуру токопровода в конце КЗ, если известны I_к, t_к, q;

2) допустимый ток КЗ I_{к доп} через токопровод, если известны t_к, q, θ_н;

3) допустимое время протекания тока I_к, если известны θ_н, q;

4) площадь поперечного сечения q токопровода, если известны I_к, t_к, θ_н, θ_к.

Изложенная методика расчёта даёт ощутимую погрешность лишь при t_к<1 с, когда нагрев апериодической составляющей тока соизмерим с нагревом от периодической составляющей /9, с.204/. При необходимости проведения более точного расчёта данную методику уточняют путём исключения второго допущения и отыскания точного значения , которое получило название теплового импульса квадратичного тока КЗ.