10. Время срабатывания электромагнитов. Время трогания и время движения.

Время срабатывания эл магнитов: t_ср=t_тр+t_дв

Процесс трогания характеризуется:

1) F_эм<F_пр, δ=δ_н=const. 2) L=L_н=W²G_μн. Уравнение эл цепи обмотки эл магнита:

Это линейное диф ур 1 порядка имеет решение:

- постоянная времени цепи обмотки эл магнита при начальном потоке якоря.

- рассчитывается из условия трогания.

Время движения характеризуется:

1) F_эм>F_пр, δ=var.

2) L=var, действует встречно напр-ю сети, i начинает убывать. Когда якорь достигает конечного положения то

После срабатывания: L_к>>L_н

Рассчитать t_дв сложно, поэтому в инженерной практике t_дв рассчитывается из первого закона Ньютона, принимая допущения:

1. F_эм нарастает по статической F_эм=f(δ) рассчитывается при установившемся токе.

2. результирующая сила действующая на якорь в течении процесса движения остаётся постоянной и среднее значение

m-масса подвижных частей

, ,

начальные условия t=0, x=0, ,

.

Данный расчет дает погрешность до (25-50)%

11. Нагрев токопровода в продолжительном режиме работы. Расчёт максимальной температуры при продолжительном режиме.

При работе ЭА в его элементах идут непрерывно три тепловых процесса: выделение тепла, поглощение тепла и отдача тепла в окружающую среду. От совокупности этих процессов зависит температура элементов ЭА.

Рассмотрим процесс нагрева однородного токопровода. Уравнение теплового баланса токопровода для любого момента времени , (2.4)

где - мощность тепловых потерь в токопроводе, Вт;

С – удельная теплоёмкость материала токопровода, Вт·с/(кг·°С);

m – масса токопровода, кг;

- превышение температуры токопровода над температурой окружающей среды (перегрев), °С; согласно ГОСТ 8024-84, наибольшая температура окружающей среды ;

S₀ – поверхность охлаждения, м²;

К_т – коэффициент теплоотдачи токопровода, численно равный количеству тепла, отдаваемому в окружающую среду за 1 с всеми видами теплоотдачи (теплопроводностью, конвекцией, излучением) с 1 м² поверхности при перегреве в 1 °С, Вт/(м²·°С).

Коэффициент теплоотдачи зависит в общем случае от температуры поверхности тела, его геометрической формы и размеров, от температуры среды, её свойств, способа конвективного теплообмена (вынужденная или естественная конвекция) и других факторов. При инженерных расчётах К_т определяют по эмпирическим формулам /2, с.5/ или таблицам /1, с.69/, полученным на основании экспериментальных исследований наиболее характерных элементов ЭА.

Уравнение (2.4) говорит о том, что энергия, выделяемая в токопроводе за время dt, равна тепловой энергии, идущей на нагрев токопровода на значение и тепловой энергии, отдаваемой в окружающую среду за время dt.

Если принять ρ, с и K_т постоянными, то при постоянстве мощности потерь решение уравнения (2.4) относительно имеет вид

, (2.5)

где - перегрев токопровода к началу процесса нагрева.

Если температура токопровода в начальный момент нагрева равнялась температуре окружающей среды ( ), то уравнение кривой нагрева принимает вид

. (2.6)

Таким образом, кривая нагрева токопровода описывается экспоненциальным законом (рис. 2.3). При перегрев достигает установившегося значения

. (2.7)

Величина, обратная коэффициенту при t в уравнении экспоненты, имеет размерность времени и называется постоянной времени. В данном случае постоянная времени теплового процесса равна , (2.8)

где cm – теплоёмкость токопровода;

K_TS₀ – теплоотдача токопровода.

Постоянная времени характеризует скорость изменения перегрева токопровода и графически определяется отрезком, отсекаемым касательной к экспоненте в начале координат от прямой . Перегрев достигает практически установившегося значения за время (3…4)T.

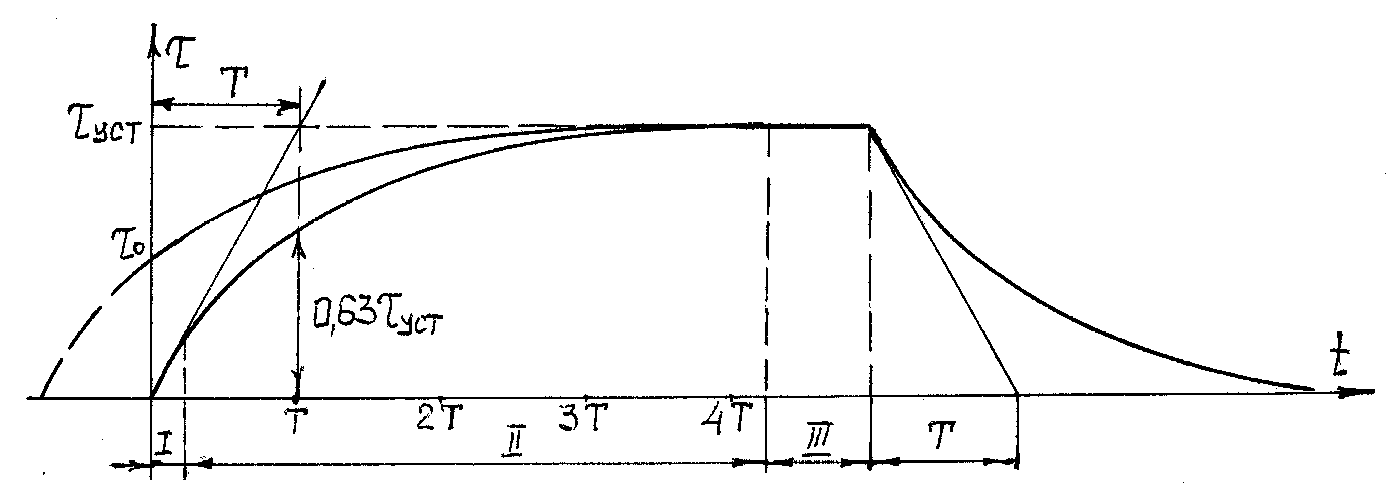
Рис. 2.3. Кривые нагрева и охлаждения однородного элемента при продолжительном режиме работы

Процесс нагрева токопровода от температуры окружающей среды до установившегося значения можно разбить на три этапа. В самом начале процесса нагрева (t<0,1T), когда перегрев ещё незначительный, ( ), теплоотдачи в окружающую среду практически нет (адиабатический процесс) и уравнение теплового баланса принимает вид

. (2.9)

Отсюда максимальная скорость нарастания перегрева равна

. (2.10)

Проинтегрировав уравнение (2.9), получим закон нарастания перегрева при адиабатическом процессе

. (2.11)

Уравнение (2.11) представляет собой уравнение касательной к экспоненте в начале координат. Поэтому можно дать следующее определение постоянной времени теплового процесса. Это отрезок времени, в течение которого перегрев тела достигает установившегося значения, если при этом отсутствует теплоотдача.

Второй этап характеризуется постепенным снижением скорости нарастания перегрева, что обусловлено постепенным увеличением количества тепла, отдаваемым токопроводом в окружающую среду.

Третий этап (t>4T) характеризуется практически прекращением дальнейшего нарастания перегрева, т. е. . При этом всё выделяющееся в токопроводе тепло идёт в окружающую среду. Поглощение тепла токопроводом отсутствует. Уравнение теплового баланса для данного этапа имеет вид

. (2.12)

Данное уравнение позволяет рассчитать допустимый ток токопровода в длительном режиме работы, приняв : , (2.13)

где - допустимый перегрев токопровода при длительном режиме работы;

R₀ – сопротивление токопровода при температуре окружающей среды;

- температурный коэффициент сопротивления материала токопровода.

После отключения токопровода тепло, накопленное в процессе нагрева, отдаётся в окружающую среду. При этом уравнение теплового баланса имеет вид

. (2.14)

Решение этого уравнения относительно перегрева

. (2.15)