Глава 2. Теории экономического роста

2.1. Становление теорий экономического роста. Важность экономического роста трудно переоценить. Эта проблема с давних пор была в центре исследований экономистов, поскольку в результате роста национального выпуска, при постоянном увеличении населения, каждый получает более высокий доход. Последний позволяет индивидам потреблять большее количество товаров и услуг, а более высокий уровень потребления обеспечивает повышение уровня жизни.

Уже в теориях меркантилистов проблема обеспечения долговременного экономического роста, которая играет ключевую роль в процветании или упадке державы, занимала центральное место.

Английская классическая школа не имела отдельной теории экономического роста. Однако она занималась факторами роста национального богатства и его соотношением с распределением дохода. Вопрос о том, чем определяется прирост национального богатства, подразумевался в самом заглавии труда А. Смита: «Исследование о природе и причинах богатства народов».

Наиболее подробно этот круг вопросов освещён в I книге «Основ политической экономии» Дж. Ст. Милля, где сначала рассматриваются все факторы производства, затем причины их роста и динамика их производительности.

Поскольку предполагалось, что величина естественных факторов производства, труда и земли в значительной степени не зависит от человеческих усилий, то в качестве основы экономического роста рассматривалось накопление − инвестирование части общественного продукта, которое приводит к возрастанию капитала. Отсюда большое значение, придаваемое «бережливости» английскими классиками, начиная с А. Смита. Поскольку основное накопление в то время производилось из прибыли капиталистов, то особое значение для экономического роста приобретала норма прибыли, а также распределение дохода, благоприятствующее капиталистам.

Что же касается нормы прибыли, то классики считали неизбежным её падение в долгосрочный период в силу действия «закона убывающего плодородия почвы», приводящего к росту ренты землевладельцев, а следовательно, к падению прибыли капиталистов, что вызывает уменьшение накопления и прекращение экономического роста.

Эту пессимистическую точку зрения отстаивали Т. Мальтус и Д. Рикардо, недооценивающие роль технического прогресса.

Схожих взглядов придерживался К. Маркс. Он доказывал тенденцию нормы прибыли к понижению в результате роста органического строения капитала. При этом он, очевидно, исходил из предпосылки, что технический прогресс может быть трудосберегающим, но не капиталосберегающим. В итоге капиталистическое производство теряет стимулы к дальнейшему росту.

С победой маржинализма возобладал статический равновесный подход, и интерес к проблемам роста снизился. Предметом этого направления в экономической теории стало распределение уже созданных редких ресурсов.

В наибольшей степени из теоретиков маржинализма проблемами экономического роста занимался А. Маршалл, который рассматривал факторы экономического роста валового и чистого дохода. Таких факторов было слишком много, а с учётом тех, которые влияют на них, теория становилась многофакторной и слишком сложной, поэтому А. Маршалл не включил её в конечный вариант «Принципов экономической науки».

Теория экономического роста развивалась в форме абстрактных моделей, обосновывающих взаимосвязь и взаимозависимость основных факторов производства и темпов его расширения. Стимул в создании такой теории – необходимость государственного регулирования роста рыночной экономики. И если сам Дж. М. Кейнс не рассматривал проблемы долгосрочного экономического роста, то его исследования послужили основанием для появления кейнсианского варианта теории экономического роста. Попытка формализовать условия экономического роста привела в 1930-е гг. к появлению моделей роста, первой из которых считается модель Харрода – Домара

2.2. Модель Харрода – Домара Англичанин Рой Харрод (1900 – 1978) и американец Евси Домар (1914 – 1997) почти одновременно разработали концепцию экономического роста в конце 30-х – 40-е гг. ХХ века. В основе её лежат две предпосылки.

Первая – рост общего выпуска определяется только одним фактором – долей инвестиций в национальном доходе. Все остальные факторы: увеличение занятости, степень использования оборудования, улучшения в организации производства, – отражающиеся на росте капиталоотдачи (У/К), исключаются.

Тогда и спрос на капитал при данной капиталоёмкости (k=К/У) или капиталоотдаче (1/k=У/К) определяется только темпом роста национального дохода.

Вторая предпосылка: сама капиталоёмкость не зависит от соотношения цен на факторы производства. Она определяется лишь техническими условиями производства, которые сохраняют её неизменной вследствие неизменного характера НТП: К/У=const.

Сбережения S есть фиксированная часть национального дохода У, определяемая неизменной нормой сбережения (s), откуда

S = sY . ( 2.2.1)

Инвестиции I равны изменению объёма капитала K, то есть

I = ∆ К. ( 2.2 .2)

Поскольку объём основного капитала К напрямую связан с национальным доходом и объёмом выпуска У через коэффициент капиталоёмкости k, то К/У=k

или ∆ К/ ∆У = k ,

откуда ∆ К = k ∆У. (2. 2.3)

Связь между долей инвестиций в национальном доходе и капиталоёмкостью строится на основе кейнсианской предпосылки о равенстве инвестиций (I) и сбережений (S): I = S. ( 2.2.4)

Из выражения (2.2.1) известно, что S=sY, а из выражений (2.2.2) и (2.2.3) cледует, что I =∆ К = k ∆У.

Отсюда равенство (2.4) между сбережениями и инвестициями можно записать следующим образом: S = sУ = k ∆У= ∆ К= I , (2.2.5)

или просто s У = k∆У. (2.2.6)

Разделив обе части равенства на У, затем на k, получим

∆У /У = s / k . (2.2.7)

Левая часть равенства (2.7) не что иное как темп роста валового продукта, т.е. темп роста экономики.

Поскольку в условиях равновесия I = S , а S = sY , темпы роста объёма выпуска и национального дохода равны темпам роста инвестиций:

∆У /У =∆ I /I = s / k.

Выражение (2.7) – это упрощённая форма известного уравнения из теории экономического роста Харрода – Домара, из которого следует, что темп роста валового продукта (и национального дохода) находится в прямой зависимости от нормы сбережений и в обратной – от коэффициента капиталоёмкости.

Основной акцент в модели сделан на темпы роста национальных сбережений, определяющих в конечном итоге и темпы экономического роста, и объёмы инвестиций в национальную экономику. Длительное время этот тезис являлся фундаментальным при разработке национальной экономической политики. Представление о том, что рост пропорционален инвестициям, не ново. Е. Домар заметил, что более раннее поколение эко­номистов, крайне озабоченных вопросами роста, – советские экономисты 1920-х гг. – уже использовали ту же идею.

Таким образом, рецепт развития был крайне прост: наращивание объёма сбережений. Специа­листы по развитию считали, что бедные страны настолько бедны, что у них нет особых надежд на рост объёма собственных сбережений. Это приводило к не­соответствию между «требуемыми инвестициями» и реальным уровнем национальных сбережений. Существующий «дефицит финансирования» в этом случае должны заполнить запад­ные доноры, что при­ведёт к достижению требуемого объёма инвестиций и, в свою очередь, обес­печит достижение целевых показателей экономического роста.

Экономисты, защищавшие данный подход, не очень хорошо понимали, сколько времени понадобится на то, чтобы помощь привела к увеличению ин­вестиций и, соответственно, к увеличению темпов роста. Но на практике они ожидали быстрых результатов: помощь этого года пойдёт на инвестиции это­го же года, что отразится на росте ВВП в следующем году.

В развивающихся странах модель роста Харрода – Домара была применена впервые при определении темпов роста первого пятилетнего плана Индии 1951 –

1956 гг. Модель была подвергнута некоторой модификации американским экономистом Х.Б. Зингером. Вскоре стало очевидным, что даже с учётом внесённых уточнений, с её помощью невозможно обеспечить качественный прогноз на будущее и тем более использовать её как инструмент для выработки экономической политики.

Основные выводы модели легли в основу теорий «большого толчка» («big push») и перехода к «самоподдерживающемуся росту». Достижение нормы накопления, достаточной для поддержания целевого темпа роста в будущем символизирует собой переход страны к «самоподдерживающемуся росту». Выводы модели широко использовались, в частности, для расчёта необходимых ресурсов, получаемых в качестве помощи от иностранных государств. Эту модель позже называли моделью «дефицита сбережений». Один из существенных недостатков модели состоит в том, что анализ факторов роста ограничен капиталом и из поля зрения выпадают естественные и трудовые ресурсы.

2.3. Модель экономического роста с двумя дефицитами. Дальнейшее совершенствование модели «дефицита сбережений» шло как в направлении её детализации и уточнения в соответствии с особенностями развивающейся экономики (учёта внешнеэкономических связей и т.п.), так и по пути разработки моделей для более низких уровней экономики развивающихся стран: секторного и отраслевого.

Модель экономического роста с двумя дефицитами (two gaps model) была разработана в 60 – 70-е гг. группой американских исследователей – X. Ченери, М. Бруно, А. Страутом, П. Экстейном, Н. Картером и др. Она представляет собой систему средне- и долгосрочных регрессивных моделей, в которых темп роста определяется в зависимости от дефицита внутренних (дефицит сбережений) либо внешних (торговый дефицит) ресурсов. Мо­дель включает три основных элемента: во-первых, расчёт необ­ходимых ресурсов, получаемых как разность сбережений (S) и инвестиций (I); во-вторых, вычисление внешнеторгового дефи­цита: экспорт (X) минус импорт (М); в-третьих, определение аб­сорбционной (поглотительной) способности, понимаемой как максимальный объём капитальных ресурсов, которые развиваю­щаяся страна способна производительно использовать в данный момент. Поэтому в статике модель можно записать следующим образом:

У ≡ Q;

У ≡ C+S+M;

Q ≡ C+I+X;

I-S ≡ M-X,

Дефицит Торговый

сбережений дефицит

где У – доход, Q – выпуск, С — совокупное потребление, S – валовые внутренние сбережения, I – валовые внутренние ин­вестиции, X – экспорт, М – импорт.

Разница между валовыми внутренними инвестициями и ва­ловыми внутренними сбережениями может быть компенсиро­вана иностранной помощью: I - S= F→I = S + F.

Разница между экспортом и импортом также может быть ком­пенсирована иностранной помощью: М - Х = F→ М = Х + F.

Объём иностранной помощи для обеспечения предусмот­ренного политикой модернизации заданного целевого темпа роста определяется наибольшим из этих двух дефицитов. По­мощь осуществляется не только для того, чтобы уменьшить внутренний и внешний дефициты, но и для того, чтобы с тече­нием времени либо вообще отказаться от иностранной помощи, либо значительно снизить её величину.

Проделанный X. Ченери и А. Страутом анализ 50 развивающихся стран показал, что средние темпы прироста сбережений составили в 1957 – 1962 гг. 6 – 8%, а максимальные – 12 – 15%. Эти последние и были приняты в качестве абсорбционной спо­собности стран «третьего мира». Максимальные темпы прироста сбережений обеспечивали при этом ежегодный темп прироста ВНП на уровне 5 – 7%. По­этому в динамике объём иностранной помощи рассчитывался по формуле

F_t = F₀ + ( β × k - α^́́׳)( Y_t –Y₀ ), (2.3.1)

где F_t – требуемый объём помощи в период времени t; β – максимально возможный темп роста инвестиций; k – приро­стный капитальный коэффициент (IСОR); α^́́׳ – предельная норма сбережений или предельная склонность к сбережениям (α^́׳ = ∆Ŝ/∆У, где ∆Ŝ – потенциальные внутренние сбережения).

Предполагается, что первая стадия модернизации закончит­ся тогда, когда темп роста инвестиций сравняется с темпом роста ВНП. Допустим, что это произойдёт в момент времени t = т. Тогда I_т = k řУ_т , где ř – целевой темп роста ВНП.

В зависимости от того, какой именно дефицит преобладает, наступает вторая или третья стадия модернизации.

Компенсировать нехватку внутренних сбережений может импорт иностранных товаров и услуг, однако целью данной стадии модернизации является обеспечение таких условий, при которых этот приток должен постепенно уменьшаться. Это дос­тигается при α^́́' > k ř, тогда S= I, М→ 0, где М – требуемый объём импорта товаров и услуг.

Для ликвидации внешнеторгового дефицита необходимо пе­рераспределить внутренние инвестиции таким образом, чтобы этот дефицит был ликвидирован. Допустим, что третья стадия модернизации начнется в момент времени t= п. Тогда

F_t= М_t-Х_t =М_n+ μ'(У_t - У_п) - Х_п(I + х)^t-n, (2.3.2)

где μ' – предельная склонность к импорту (μ' = ∆М/∆У); х – темп роста экспорта, рассчитанный экзогенно (характеризует меры государства по стимулированию экспорта).

Дефицит торгового баланса будет ликвидирован, если х > ř, а μ'< μ_ср, где μ_ср – средняя склонность к импорту. Достаточ­ный объём сбережений находится как

S= I - F_t = k řУ_t - F_t . (2.3.4)

Рост объёма потенциальных сбережений не только обеспе­чит внутренние потребности в капиталовложениях, но и позво­лит со временем полностью отказаться от иностранной помощи (если Ŝ > I ).

Решая проблему нехватки сбережений, экономика одновременно избавляется от торгового дефи­цита и, наоборот, решая проблему нехватки торгового дефицита, одновременно решает проблему дефицита сбережений. Всё зависит в конечном счёте от правильного выбора целевого темпа роста ВНП и мер, которые обеспечивают его достижение. Поэтому существует такая точка, в которой стратегии пересека­ются, она и определяет целевой темп роста ВНП.

Описанная модель модернизации была разработана для Из­раиля. В дальнейшем она была значительно усовершенствована и широко применялась для определения размеров иностранной помощи в странах Азии и Латинской Америки. В 1972 г. X. Че­нери и Н. Картером была осуществлена корректировка модели с целью показать влияние прироста иностранных ресурсов и экспорта на размеры внутренних сбережений. Поэтому форму­ла для определения потенциальных сбережений была уточнена:

Ŝ = S₀ + Ŝ₁ × У+ Ŝ₂× F + Ŝ ₃ × X , (2.3.5)

где Ŝ₁, – предельная склонность к сбережениям; Ŝ₂, Ŝ ₃ – коэф­фициенты, отражающие влияние прироста иностранных ресур­сов (F) и экспорта (X) на размер внутренних сбережений (S).

По принципу теоретической модели с двумя дефицитами в 70-е гг. было составлено около 30 практических моделей модер­низации для ЮНКТАД (Конференция ООН по торговле и развитию) и 10 – для ЭСКАТО (Экономическая и социальная комиссия ООН для Азии и Тихого океана).

Модель с двумя дефицитами есть дальнейшая конкретиза­ция идеи «большого толчка». Её цель – проследить взаимо­связь развития внутреннего накопления и внешних источников финансирования. Она явно недооценивала внутренние ресур­сы развивающихся стран, что объективно вело к завышению потребности в иностранной помощи и в конечном счёте – к стремительному росту внешнего долга. Усиление внешнеэко­номической зависимости вызвало резкую критику кейнсианской модели со стороны леворадикальной политической эконо­мии.

Рассмотренные модели экономического роста были ориентированы на использование такого ограниченного в развивающихся странах фактора, как капитал, и явно не учитывали возможности использования такого относительно избыточного фактора, как труд. Это и определило справедливую критику неокейнсианского направления со стороны неоклассиков.

Ещё одним заметным недостатком этой модели является фактическое обоснование вмешательства стран-доноров во внутренние дела стран-должников. Существенным недостатком оказался весьма агрегированный (приблизительный) характер модели. В условиях ограниченности и ненадёжности статисти­ческой информации многие важные показатели модели (напри­мер, определение абсорбционной способности экономики раз­вивающихся стран) носят чрезвычайно условный характер, что снижает ценность полученных с их помощью прогнозов и ре­комендаций.

2.4. Модель Р.Солоу. В 1950-е гг. было обращено внимание на тот факт, что модель Харрода – Домара позволяет описать лишь кратко­срочный экономический рост, поскольку в долговременной перс­пективе рост ВНП ограничивается темпами роста населения (или рабочей силы). Реакцией на это открытие явилось создание в 1957 г. американским экономистом лауреатом Нобелевской премии Робертом Мертоном Солоу (р. 1924), неоклассической моде­ли экономического роста. В отличие от посткейнсианских моделей роста в неоклассических коэффициент капиталовооружённости труда не является постоянным, а меняется в зависимости от состояния конъюнктуры. Для этого кроме технической взаимозаменяемости факторов производства необходима предпосылка неоклассической концепции о господстве совершенной конкуренции на рынках факторов. Отсюда происходит название этих моделей.

В своей модели Р. Солоу использовал классическую производственную функцию Кобба – Дугласа:

У = К^aL^1-а,

где У – объём выпуска, К – капитал, L – труд и 0 < а < 1, и трансфор­мировал её, введя технологическую константу А: У = А∙ К^a∙L^1-а. Воз­действие технического прогресса в модели Солоу выражается в приросте эффективности труда, который происходит с постоян­ным темпом. Предполагается, что данный тип технического про­гресса должен вывести на устойчивый уровень капиталовоору­жённости, обеспечивающий постоянную эффективность труда.

Предложение в этой модели описывается производственной функцией Кобба – Дугласа, в которой труд и капитал являются хорошими субститутами и сумма коэффициентов эластичности выпуска по факторам равна единице (постоянная от масштаба):

Y = F (K₁L) = K^ L^1-,

то есть m Y_t = f (m K_t, m L_t),

пусть , тогда ,

отсюда видно, что объём производства на одного работника _, является функцией капиталовооружённости одного работника .

Условимся, что будем использовать малые буквы для тех количественных показателей, которые относятся к одному рабочему:

– производительность труда;

– капиталовооружённость труда.

Тогда производственную функцию можно записать y = f(k), где f(k) = F(k,1), то есть производительность работника определяется его капиталовооружённостью. Построим график этой производственной функции (рисунок 2.4.1):

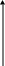y f(k)

Выпуск на одного

работника

 MP_k

1

0 k Капиталовооружённость

одного работника

Рисунок 2.4.1 – Производственная функция

tg  = MP_k, то есть тангенс угла наклона данной производственной функции показывает, сколько дополнительной продукции на одного работника можно получить, если увеличить капиталовооружённость на одну единицу. Угол наклона функции уменьшается, то есть она характеризуется понижающейся предельной производительностью капитала.

Солоу упрощает анализ экономики, предполагая, что нет государства и внешней торговли. Тогда спрос на произведённый продукт – это спрос со стороны домохозяйств (потребителей) и фирм (инвесторов), то есть продукция, произведённая каждым работником делится между потреблением и инвестициями, в расчёте на одного рабочего: y = c + i , а функция потребления

с = (1-S) Y, (2.4.1)

где S – норма сбережения _. Отсюда

Y = (1-S) y + i , упрощая получаем i = s y.

Таким образом, инвестиции (как и потребление) пропорциональны доходу.

Если i = s, норма сбережений s также показывает, какая часть произведённой продукции направляется на капиталовложения.

Представив две главных составляющих модели Солоу – производственную функцию и функцию потребления, можно проанализировать, как накопление капитала обеспечивает экономический рост.

Запасы капитала могут меняться по двум причинам:

• инвестиции приводят к росту запасов капитала;

• часть капитала изнашивается, то есть амортизируется, что приводит к уменьшению запасов капитала.

Инвестиции в расчёте на одного работника i = sy, а y = f(k), тогда i = s f(k). Отсюда, чем выше уровень капиталовооружённости (k), тем выше объём производства f(k) и больше инвестиции (i).

Представим графически (рисунок 2.4.2):

f(k)

y

c

sf(k)

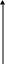y

i

0 k k

Рисунок 2.4.2 – Производство, потребление и инвестиции

Хорошо видно, как норма сбережений (s) определяет разделение продукта на потребление и инвестиции для каждого из значений капиталовооружённости.

Чтобы учесть в модели амортизацию, предполагаем что ежегодно выбывает определённая доля капитала –  – норма выбытия. (Например, если станок служит 10 лет, то  = 0,1, а если 5 лет, то  = 0,2).

Таким образом ежегодно выбывающее количество капитала =  k. Из графика видно, что выбытие пропорционально запасам капитала (рисунок 2.4.3).

Тогда изменение запасов капитала на 1 работника (k)

k = i - s k , так как i = s f(k),

отсюда Dk = s f(k) - s k

Покажем графически:

s k

i

А sf(k)

i* = s k* s k

i₁

s k₁

0 k₁ k* k

Рисунок 2.4.3 – Инвестиции, выбытие и устойчивый уровень капиталовооружённости

В точке А выбытие капитала компенсируется инвестициями s k = s f(k), поэтому k* – единственный уровень капиталовооружённости, который не будет меняться во времени. Тогда k* – устойчивая капиталовооружённость. Устойчивый уровень капиталовооружённости соответствует равновесию экономики в долгосрочном плане. Независимо от первоначального объёма капитала, с которым экономика начинает развиваться, она достигает затем устойчивого состояния. Докажем это.

Пусть k₁ < k*, при k₁, как видно на графике i₁ > s k₁, следовательно капиталовооружённость растёт, что приводит к росту производства до тех пор, пока не приблизится к устойчивому уровню капиталовооружённости (k*).

При k₂ > k* всё будет происходить наоборот.

Таким образом, если экономика не находится в устойчивом состоянии, то независимо от размера капитала на одного работающего начинают действовать силы, приводящие её к долгосрочному устойчивому равновесию. Параметр, обеспечивающий равномерный рост в модели Солоу – капиталовооружённость труда. Динамические системы, в которых переменные обладают свойством автоматически возвращаться к состоянию устойчивого равновесия, называются стабильными системами. То есть модель роста Солоу описывает стабильный динамический процесс роста.

Может ли более высокий уровень сбережений обеспечить высокий экономический рост?

Рассмотрим, что происходит в экономике с изменением нормы сбережений. Пусть норма сбережений (S) растёт с S₁ до S₂ (рисунок 2.4.4)

s k

i s k S₂ f(k) = i₂

S₁ f(k) = i₁

0 k₁ k₂ k

Рисунок 2.4.4 – Рост нормы сбережений

После увеличения нормы сбережений с S₁ до S₂ инвестиции возрастают, но инвестиции больше выбытия (I_i > s k₁), что приводит к росту капитала до тех пор, пока экономика не достигает нового устойчивого состояния k c большей капиталовооружённостью и более высокой производительностью труда, чем в исходном периоде.

Модель Солоу показывает, что норма сбережений является ключевой детерминантой величины устойчивой капиталовооружённости. Следовательно, если норма сбережений более высока, то экономика будет иметь при прочих равных условиях больший запас капитала и более высокий уровень производства.

Теоретические выводы подтверждаются эмпирическими данными: страны, которые направляют значительную часть дохода на сбережения (и инвестиции), имеют более высокий уровень душевого дохода.

Существует ряд устойчивых состояний экономики в зависимости от нормы сбережений. Какое же является наилучшим? Очевидно, что конечной целью экономического роста является увеличение экономического благосостояния общества, т.е. наиболее высокий уровень потребления.

Уровень накопления капитала, обеспечивающий устойчивое состояние с наивысшим уровнем потребления, называется золотым уровнем накопления капитала.

Чтобы найти потребление в устойчивом состоянии, вспомним, что y = c + i, тогда c = y – i. Заменим значением y и i на их величины в условиях устойчивого уровня капиталовооружённости y = f(k*),

при этом I = s k*, тогда

с* = f(k*) - s k*. (2.4.2)

Устойчивый уровень потребления есть разница между выпуском и выбытием капитала в устойчивом состоянии. Повышение капиталовооружённости двояко воздействует на величину потребления:

• способствует росту выпуска продукции;

• требует всё больше продукции для возмещения выбытия капитала (рисунок 2.4.5)

s k*

f(k*)

П роизводство

и выбытие

к апитала в

устойчивом с**

с

i

остоянии

0 k** k*

Рисунок 2.4.5 – Устойчивый уровень потребления

Видно, что существует единственный уровень капиталовооружённости – уровень золотого правила k**, при котором душевое потребление достигает максимального значения.

К этому же выводу можно прийти другим путём.

k* – начальная капиталовооружённость. Пусть она увеличивается до k*+1, тогда объём дополнительного выпуска продукции

D y = f(k* + 1) – f(k*), (2.4.3)

правая часть равенства не что иное, как предельный продукт капитала (МP_K).

Если Dk = 1, то прирост выбытия равен норме выбытия, то есть s. Чистый эффект от дополнительной единицы капитала равен увеличению потребления

D с = MP_K - s. (2.4.4)

В условиях золотого правила накопления потребления максимально. То есть любой другой запас капитала приводит к уменьшению потребления. Поэтому следующее условие составляет само золотое правило:

MP_K = s. (2.4.5)

По-другому, если выполняется золотое правило, то MP_K - s = 0.

Мы рассмотрели базовую модель Солоу, но для объяснения фактических темпов роста, которые имеет та или иная страна, необходимо включить в модель другие источники экономического роста: рост населения и технологический прогресс.

Рост численности работников ведёт к сокращению капиталовооружённости каждого из них. Пусть темп роста населения равен темпу роста рабочей силы:

n =DL/L. Изменение запаса капитала, приходящегося на одного работника, будет определяться следующим образом:

Dk = i - sk – nk.

Помня, что i = s f(k), преобразуем Dk = s f(k) – (s + n)k.

Составляющая (s + n)k может рассматриваться как критическая величина инвестиций. Это инвестиции, необходимые для поддержания запаса капитала, приходящегося на одного работника, на постоянном уровне.

Тогда график устойчивой капиталовооружённости с усложнением модели может быть представлен следующим образом (рисунок 2.4.6):

(s + n)k

i sf(k)

0 k* k

Рисунок 2.4.6 – Рост населения в модели Солоу

Рассмотрим две страны, в которых население увеличивается разными темпами: n₁ и n₂, причём n₁ < n₂ (рисунок 2.4.7):

i ( + n₂)k ( + n₁)k sf(k)

0 k₂ k₁ k

Рисунок 2.4.7 – Влияние роста населения

Графически ясно, что более высокие темпы роста населения вызывает тенденцию обнищания страны, поскольку уровень капиталовооружённости сокращается, а следовательно, уменьшаются и объёмы выпуска и доходы. Эмпирические данные совпадают с выводами модели Солоу и свидетельствуют, что темп роста населения является одной из детерминант уровня жизни в стране.

Теперь включим в модель технический прогресс. Предполагается трудосберегающая форма технического прогресса. Предполагается, что технический прогресс осуществляется путём роста эффективности труда Е с постоянным темпом g. Тогда (L E) – численность условных единиц труда с постоянной эффективностью Е. Чем больше Е, тем больше продукции может быть произведено данным числом работников.

Тогда , а .

В состоянии устойчивого равновесия уровень капиталовооружённости k* уравновешивает, с одной стороны, влияние инвестиций, повышающих фондовооружённость, а с другой стороны, воздействие выбытия, роста числа занятых и технологического прогресса, снижающих уровень капитала в расчёте на эффективную единицу труда:

k = s f(k¢) – ( + n + g) k¢. (2.4.6)

Как нам известно, капитал на единицу труда с постоянной эффективностью k в устойчивом состоянии неизменен.

Если Dk = 0, то

s f(k¢) = ( + n + g) k¢. (2.4.7)

Вспомним, что количество единиц труда, с постоянной эффективностью приходящихся на одного работника, растёт с темпом g. Следовательно, выпуск на одного работника Y/L = y E также растёт темпом g.

Модель Солоу показывает, что только технологический прогресс может объяснить непрерывно растущее благосостояние.

С учётом технологического прогресса изменяются условия выполнения «золотого» правила. Теперь устойчивый уровень потребления максимизируется, если MP_K = s + n + g или MP_K - s = n + g. (2.4.8)

Рассмотренная нами модель носит довольно общий характер и не учитывает целый ряд реальных ограничений экономического роста (социальных, экологических и т.д.) Несмотря на это, было предпринято несколько попыток конкретизации анализируемой модели на примере стран третьего мира.

Применение модели в чистом виде для развивающихся стран не может дать такие же результаты, как и в развитых странах, поскольку в ней делается акцент на капиталоёмких технологиях (типичных для развитых стран), а основа технического прогресса видится прежде всего в роста капиталовооружённости труда. В 80 – 90-е годы предпринимались попытки уточнить и дополнить модель Солоу. В частности, путём включения в неё человеческого капитала. Эти попытки принадлежат Р. Лукасу, Г. Мэнкью, Д. Ромеру и Д. Уэйлу.

2.5. Модель Солоу и проблема сходимости. Важное значение в модели Солоу имеет тезис о сходимости (конвергенции). Действительно, если две страны имеют одинаковую производственную функцию, темп роста населения (N), норму выбытия (σ) и норму сбережения (S), то очевидно, что они стремятся к одному и тому же уровню капиталовооружённости k^*. Поскольку их устойчивые состояния совпадают, бедная страна будет расти быстрее. Таким образом, бедная страна в конце концов достигнет уровня развития богатой.

Существуют различные подходы к проблеме конвергенции. Концепция абсолютной конвергенции предполагает, что бедные страны растут быстрее богатых и разница уровня среднедушевого дохода постепенно снижается независимо от характеристик экономики. Обычно рассматривается два типа абсолютной конвергенции: 1) β – конвергенция означает, что для относительно более бедных стран характерны более высокие темпы роста, чем для богатых; 2) δ – конвергенция означает уменьшение разброса в подушевом доходе с течением времени.

Можно показать, что наличие β – конвергенции не предполагает обязательно, что будет иметь место δ – конвергенция.

Естественно, что развивающаяся страна имеет первоначальный уровень капиталовооружённости (k₁) более низкий, чем развитая (k₂), и обе страны имеют уровень капиталовооружённости ниже равновесного(k^*): k₁< k₂ < k^*. Это означает, что она должна иметь первоначально и более высокие темпы роста капиталовооружённости: g _k1 > g _k2 (рисунок 2.5.1). Очевидно, что по мере приближения к устойчивому уровню капиталовооружённости темп прироста капиталовооружённости будет уменьшаться, а следовательно, будет уменьшаться и темп роста экономики в целом.

sf(k)

g _k1

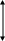
g _k2

n + δ

sf(k) (k)

k₁ k₂ k^*

k

0

Рисунок 2.5.1 – Гипотеза о строгой (абсолютной) сходимости

Гипотеза о строгой (абсолютной) сходимости объясняет тот факт, что при наличии указанных выше предпосылок страны с первоначально меньшим запасом капитала развиваются быстрее, чем страны с большим первоначальным

запасом капитала. Однако на практике такая абсолютная сходимость маловероятна. Существующие эмпирические исследования не подтверждают наличия абсолютной конвергенции. Поэтому обычно для проверки модели Солоу исходят из гипотезы о слабой (условной) конвергенции (сходимости). Это означает, что каждая страна имеет свой устойчивый уровень капиталовооружённости (k₁^*< k₂^*), т.е. снимается предпосылка об одинаковой норме сбережения, оставляя все другие без изменения.

Гипотеза условной конвергенции предполагает, что бедные страны растут быстрее богатых при прочих равных (при условии схожести структурных параметров и производственной функции), т.е. при одинаковом устойчивом состоянии. В случае если устойчивые состояния отличаются, условная конвергенция означает, что страна растёт тем быстрее, чем дальше она находится от собственного устойчивого состояния.

Если норма сбережения в развивающейся стране (s₁) меньше, чем норма сбережения в развитой стране (s₂), то темп прироста капиталовооружённости может быть больше, меньше или равен темпу прироста капиталовооружённости в развитой стране. При этом сходимость достигается отнюдь не всегда. Страна с более низким первоначальным запасом капитала может иметь более низкие темпы роста, чем страна с более высоким, если её устойчивый уровень также ниже.

Попытки эконометрических проверок наличия конвергенции с использованием выводов модели Солоу дают противоречивые результаты. Мэнкью, Ромер и Уэйл, используя базу данных, в которой представлена очень широкая выборка стран, получили статистически значимое направление связи темпов роста выпуска с нормой сбережений и темпами роста населения, предсказанное моделью Солоу. Однако количественно влияние этих показателей оказалось выше, чем оценки, рассчитанные по модели. Был сделан вывод о том, что модель Солоу не даёт возможности учесть ряд важных факторов, вызывающих различие в уровне жизни богатых и бедных стран. Одним из основных направлений критики модели Солоу является экзогенность ключевых факторов экономического роста, таких как темпы роста научно-технического прогресса, норма сбережений и темп роста населения(s, s, n, g). Поэтому позже это дало возможность квалифицировать экономический рост как экзогенный и эндогенный.

2.6. Новые теории роста. Традиционно в качестве основных факторов производства рас­сматривали землю, капитал, труд. Факторам, обеспечивавшим прогресс общественного производства за счёт создания и приведения в действие интеллектуальных ресурсов, отводили роль внешних (экзогенных) по отношению к экономическому ро­сту.

По мере возрастания роли качества человеческого капитала в производстве появляется необходимость адекватного отраже­ния этого фактора в экономической теории. Результатом стало введение в экономические модели фактора научно-техническо­го прогресса, соединяющего в себе все качественные аспекты роста эффективности традиционных факторов производства.

П. Ромер, Р. Лукас и другие сторонники «новых теорий роста» рассматривают научно-технический прогресс как внутренний, эндогенный фактор экономического роста и в значительной мере опираются на концепцию человеческого капитала. Выделяются три направления, по которым осуществляются инвестиции, обес­печивающие экономический рост: вклады в новое знание, вкла­ды в человеческий капитал и промежуточные расходы, нацелен­ные на распространение знаний и умений.

В 80 – 90-е годы Р. Лукас одним из первых попытался оценить вклад человеческого капитала в экономический рост. При предположении о равенстве темпов роста физического и человеческого капитала (в условиях динамического равновесия) Лукас делает вывод о том, что темп роста выпуска будет полностью определяться ростом человеческого капитала.

П. Ромер и его последователи разработали модель индуст­рии знания, которая обеспечивает экономический рост, произ­водя новые идеи. Основные положения этой теории таковы:

• Каждая новая идея требует определённой суммы инвестиций в нематериальные активы (типа НИОКР).

• Эта сумма снижается со временем, поскольку производящая знание индустрия может эксплуатировать постоянно увеличивающийся запас знаний и умений или, что то же самое, производить при неизменных инвестициях большее количе­ство идей.

• Индустрия знания является ёмкой в отношении человеческого капитала и использует существующий запас знания как ввод.

• Цена новых идей определяется объёмом инвестиций, идущих в индустрию знания, а также интенсивностью и эффективностью их использования.

• Более дешевые новые идеи поднимают макроэкономическую производительность и благосостояние потребителей вслед­ствие большего выбора и лучшего качества.

Накопление человеческого капитала рассматривается « новы­ми теориями роста» как результат деятельности системы образо­вания. Она обеспечивает технологический прогресс, потому что затраты на образование увеличивают запас челове­ческого капитала и таким образом улучшают способность экономики производить новые идеи и дают ей сравнительные пре­имущества в наукоёмких производствах.

С другой стороны, индустрия образования использует челове­ческий капитал как инвестиции. Эти инвестиционные расходы состоят в значительной степени из заработной платы преподава­телей и затрат на формирование материально-технической базы образования.

«Новые теории роста» уделяют особое внимание распростра­нению знаний и умений. Этот процесс, в отличие от распределе­ния и потребления обычных благ, характеризуется рядом особенностей. В данном случае имеются в виду эффекты накопления и распространения знаний. Инвести­ции в науку и образование создают условия для качественного прорыва к новым открытиям и их практического приложения. Распространение существующего знания «вширь» вызывает межотраслевые эффекты, выражающиеся в освоении новых тех­нологических принципов в тех отраслях производства, где они до сих пор не находили применения. Наконец, накопление и распространение знаний ведут к общему подъёму общественно­го сознания и культуры народа, изменяя его мировоззрение, быт, отношения с природной средой.

Как специфический продукт науки и образования знание включается в процесс общественного производства в разных фор­мах. Включение знания в процесс производства общественного продукта, или эксплуатация знания, связано со значительны­ми затратами. Эксплуатация знания означает его превращение в форму продукта, технологии, квалификации, новое качество организации. Конечный эффект выражается в росте производи­тельности труда, снижении издержек, приросте доходов. Зат­раты фирмы, связанные с эксплуатацией знаний, объективно ограничены не только её финансовыми возможностями, но и предполагаемым соотношением между затратами и результата­ми, так как фирма не может позволить себе затраты с уровнем окупаемости ниже общественно нормального. Поэтому часть затрат по эксплуатации знаний и в ещё большей степени по их производству относится к категории общественных расхо­дов и финансируется за счёт бюджетных и иных целевых источ­ников.

Сторонники «новых теорий роста» доказали, что устойчивый экономический рост возможен лишь как эндогенный рост, то есть основанный на увеличении человеческого капитала, которым располагает страна. Причём из этого следует, что низкое качество физического капитала или его относительный недостаток может быть компенсировано инвестициями в человеческий капитал (в качестве примеров приводятся Южная Корея и Тайвань). Именно человеческие ресурсы в развивающихся странах определяют социально-экономическое развитие. Причём в экономике должны быть созданы условия для эффективного использования человеческого капитала.

2.7. Модель Лукаса. В модели выпуск описывается производственной функцией Кобба – Дугласа вида

Y_t = ĀK_t^α(LH_t) ^1-α ,

где 0 < α < 1; Ā – технологический параметр, Ā > 0; H_t – уровень человеческого капитала репрезентативного агента в экономике в момент времени t (т.е. уровень человеческого капитала, которым обладает типичный представитель рабочей силы).

Как и в модели Солоу, численность населения и рабочей силы совпадают, в этом варианте численность населения неизменна, поэтому совокупный запас человеческого капитала равен LH_t. При такой интерпретации эффективность труда измеряется уровнем человеческого капитала. Производственная функция, как и в модели Солоу, описывает экономику с постоянной отдачей от масштаба. Инвестиции в момент t представляют собой сумму инвестиций в физический (I_t^k) и человеческий (I_t^h) капитал: I_t = I_t^k + I_t^h.

Равновесие на рынке товаров и услуг, как и в модели Солоу, описывается уравнением Y = C + I.

Нормы амортизации физического и человеческого капитала совпадают, поэтому K = I ^k – δK; H = I ^h - δH.

В модели предполагается полная взаимозаменяемость капитальных ресурсов. Поэтому поскольку издержки накопления физического и человеческого капитала совпадают, в устойчивом состоянии их предельные производительности также должны уравниваться, т.е. должно выполняться условие MPK = MPH. Отсюда

αĀ ^1-α = (1–α)Ā α L . (2.7.1)

Из (2.7.1) следует, что

= (2.7.2)

С учётом (2.7.2) производственная функция принимает вид:

Y = AK, (2.7.3)

где A = Ā L ^{(1 – α)} .

Модель (2.7.3) получила название «модель AK». Её основным свойством является постоянная предельная производительность капитала, в отличие от модели Солоу, в которой используется свойство убывающей предельной производительности факторов. Эта постоянная отдача становится возможной благодаря тому, что капитал понимается в широком смысле, т.е. включает в себя не только физический, но и человеческий капитал.

Все остальные предпосылки модели Солоу остаются в силе. Поэтому выпуск на душу населения можно представить в виде

y = ƒ (k) = Ak,

где k – капиталовооружённость одного работника.

Поскольку k = i – δk = sAk – δk, темп роста капиталовооружённости равен

= s – δ = sA – δ при любом значении k. (2.7.4)

В модели не рассматриваются темпы роста технологического прогресса и роста населения, так как её задача показать, что постоянный рост можно объяснить без экзогенно заданных технологических изменений.

На рисунке 2.7.1 темп роста капиталовооружённости при любом её уровне – это расстояние между горизонтальными линиями sA и δ. Если sA > δ, то > 0 и капиталовооружённость растёт с постоянным темпом.

sA,  sA



0 k

Рисунок 2.7.1 – Темпы роста капиталовооружённости в модели AK

Поскольку y = AK, а потребление с = (1 –s) y, то очевидно, что темпы роста производительности труда, потребления на одного работающего совпадают

= = = sA - . (2.7.5)

Таким образом, в рассматриваемой модели постоянный экономический рост возможен без технологического прогресса. Причём в отличие от модели Солоу, увеличение нормы сбережений приводит к тому, что темпы роста увеличиваются не временно, а постоянно. Снижение нормы амортизации также приводит к устойчивому повышению темпов экономического роста.

Из (2.7.3) следует, что A представляет собой как предельную, так и среднюю производительность капитала. Поэтому условие (2.7.5) означает, что если та часть капиталоотдачи, которая идёт на накопление капитала, превышает норму выбытия, то в экономике будет наблюдаться устойчивый экономический рост. Темпы роста увеличиваются при технологических изменениях, ведущих к росту параметра A, т.е. повышающих среднюю и предельную производительность капитала.

Модель AK предсказывает отсутствие как абсолютной, так и относительной конвергенции. Её анализ позволяет сделать следующий вывод. Если две страны имеют одинаковые производственные функции, нормы сбережений и нормы амортизации, но отличаются первоначальным уровнем запаса капитала, то капиталовооружённость, производительность труда и потребление на одного работника в этих странах будут расти с одинаковым темпом (sA – ), т.е. сближение уровней жизни происходить не будет. Этот результат – следствие постоянной предельной производительности капитала. Он ставит под сомнение адекватность модели, так как эмпирические наблюдения показывают наличие условной конвергенции. Это обстоятельство побудило к созданию модификации модели AK, оставляющей в силе постоянный темп экономического роста в долгосрочной перспективе (без использования предпосылки об экзогенном технологическом прогрессе), однако предсказывающей условную конвергенцию.

Рассмотрим уравнение, описывающее темп роста капиталовооружённости:

= s – δ. (2.7.6)

По определению, если устойчивое состояние существует, то соответствующий ему темп роста капиталовооружённости является константой. Из (2.7.6) видно, что для того, чтобы эта константа была положительной (а не нулевой, как в модели Солоу), необходимо и достаточно, чтобы выполнялось условие

 . (2.7.7)

Таким образом, (2.7.7) является необходимым и достаточным условием постоянного эндогенного роста. Если , то по правилу Лопиталя

= , т.е. при неограниченном росте k средняя и предельная производительности капитала совпадают. Тогда из (2.7.7) следует, что для наличия постоянного эндогенного роста необходимо и достаточно, чтобы выполнялось условие:

>  0 (2.7.8)

Выражение (2.7.8) означает, что отдача капитала со временем перестает быть убывающей и становится постоянной. Производственная функция, обладающая свойством (2.7.8), может быть представлена функцией вида

Y = F (K, L) = AK + BK^α L^1-α, (2.7.9)

где A > 0, B > 0 , 0 > α > 1.

С учётом постоянной отдачи от масштаба в расчёте на душу населения можно переписать (2.7.9) в виде

y = ƒ (k) = Ak + Bk^α. (2.7.10)

Отсюда

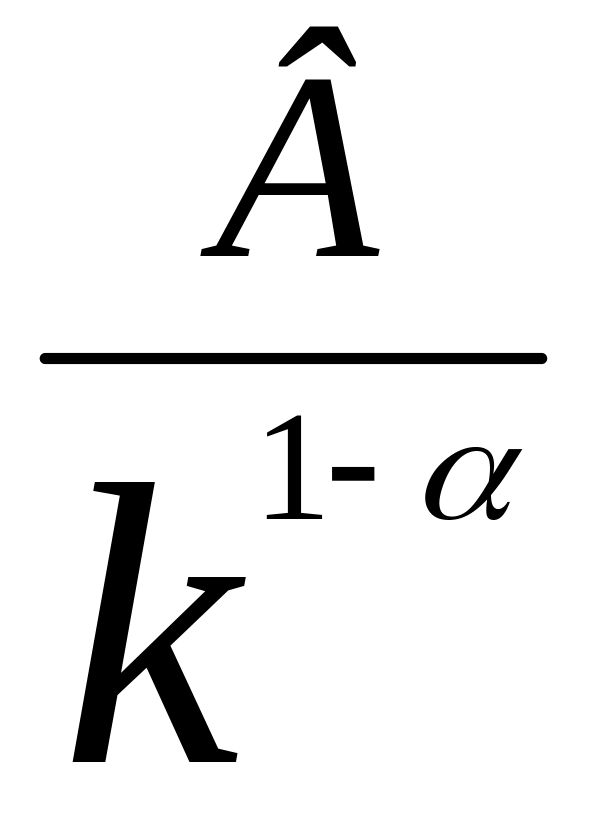. (2.7.11)

Из (2.7.11) видно, что средняя производительность капитала падает с ростом капиталовооружённости, а при её неограниченном росте стремится к А.

С учётом (2.7.11) темп роста капиталовооружённости (при отсутствии технологического прогресса и постоянном населении) равен

= s – δ = sA + . (2.7.12)

Выражение (2.7.12) показывает, что с ростом капиталовооружённости темп её роста падает, а при неограниченном возрастании k темп роста капиталовооружённости стремится к постоянной величине (sA = δ ). Если sA > δ, то темп роста k в устойчивом состоянии положителен, т.е. наблюдается постоянный эндогенный рост.

В этом случае будет также наблюдаться и условная конвергенция. Пусть в двух странах С и В производственная функция и все параметры совпадают, но в стране C первоначальный уровень капиталовооружённости ниже (k_c < k_d).

Тогда в устойчивом состоянии обе страны будут расти с одинаковым темпом (sA – ), но первоначально темп роста в C будет выше:

+ – δ > sA + s – δ. Иными словами, чем дальше страна отстоит от устойчивого уровня, тем выше темпы экономического роста. По мере накопления капитала темпы роста падают, и, в конце концов, страны приближаются к одинаковому устойчивому уровню. В соответствии с определением это означает, что имеет место условная конвергенция.

2.8. Модель Ромера. В модели Лукаса используется расширение понятия «капитал» за счёт включения в него помимо физического ещё и человеческого капитала. Одним из альтернативных способов расширения понятия капитала для получения эндогенного роста является интерпретация Ромера, предложившего рассматривать капитал как комбинацию физического капитала и продукта инвестиций в исследования и разработки (R&D). Таким продуктом могут, например, считаться идеи по производству новых товаров или по совершенствованию технологии производства уже имеющихся. Эти идеи являются, в частности, побочным продуктом инвестиций, так как фирма, увеличивая физический капитал, обучается одновременно более эффективному его использованию, этот эффект получил название «обучение на опыте» («learning – by – doing»). Часть подобного капитала порождает внешние эффекты (экстерналии), так как фирма может узнать, как произвести новый продукт или улучшить технологию производства старого, наблюдая за деятельностью других фирм. Таким образом, выпуск фирмы, помимо обычно включаемых в производственную функцию ресурсов, зависит также от общего уровня знаний (технологий) в экономике.

В модели Ромера используется производственная функция Кобба – Дугласа, причём производственная функция репрезентативной функции имеет вид:

, 0<α<1, β>0. (2.8.1)

где  соответственно выпуск, капитал и трудовые ресурсы репрезен-тативной фирмы в момент времени t;

A_t  уровень технологии в экономике.

Показатель A_t растет с ростом общего уровня знаний. Другими словами, A_t растет вместе с общим запасом капитала K_t,, так как с его ростом происходит обучение на опыте. Поэтому в этой модели в качестве аппроксимации уровня знаний служит общий запас капитала. A_t = K_t, где K_t – совокупный запас капитала в экономике в момент времени t.

Пусть в экономике действует N подобных фирм. Тогда K_t = N и выпуск в экономике описывается производственной функцией:

Y_t = K_t^αL_t^1-αK_t^β, 0 < α < 1, β > 0. (2.8.2)

Норма сбережений s и норма выбытия капитала δ задаются, как и в модели Солоу, экзогенно. Темп роста населения равен n.

В экономике наблюдается возрастающая отдача от масштаба, так как

α+(1–α)+β=(1+β) >1, однако это не обязательно означает отсутствие совершенной конкуренции, так как экономия от масштаба может достигаться за счёт экстерналий.

Изменение запаса капитала описывается следующим образом:

= sY – δK.

Отсюда и, следовательно, в устойчивом состоянии Y и K растут одинаковым темпом. Темп роста выпуска

.

Так как в устойчивом состоянии , то

.

Отсюда (2.8.3)

Из (2.8.3) следует, что если числитель и знаменатель в правой части не равны 0, то в устойчивом состоянии рост обеспечивается за счёт роста населения. Если

n > 0 и β = 1 – α, темпы роста будут стремиться к бесконечности.

В случае, когда (α + β) > 1, темпы роста также будут стремиться к бесконечности, так как

.

Во всех этих случаях мы сталкиваемся с экзогенным ростом, так как экономический рост зависит от темпа роста населения, а он задаётся в модели экзогенно.

Единственная возможность для эндогенного роста остаётся в случае, если n = 0 и β = 1 – α.

Тогда . (2.8.4)

Выражение (2.8.4) показывает, что в этом случае наблюдается постоянный эндогенный рост, причём его темпы зависят от нормы сбережений и постоянной численности населения. Из (2.8.4) следует, что темпы роста капитала не зависят от его величины, т.е. эта модель не предполагает ни абсолютной, ни условной конвергенции.

2.9. Модель заимствования технологий. Рассмотренные модели технологического прогресса подходят для развитых стран. Для большинства развивающихся стран проблема заключается не в решении, тратить или не тратить ресурсы на нововведения, а в вопросе, перенимать ли технологии, развитые другими. Рассмотрим модель заимствования технологий.

Пусть производственная функция имеет вид

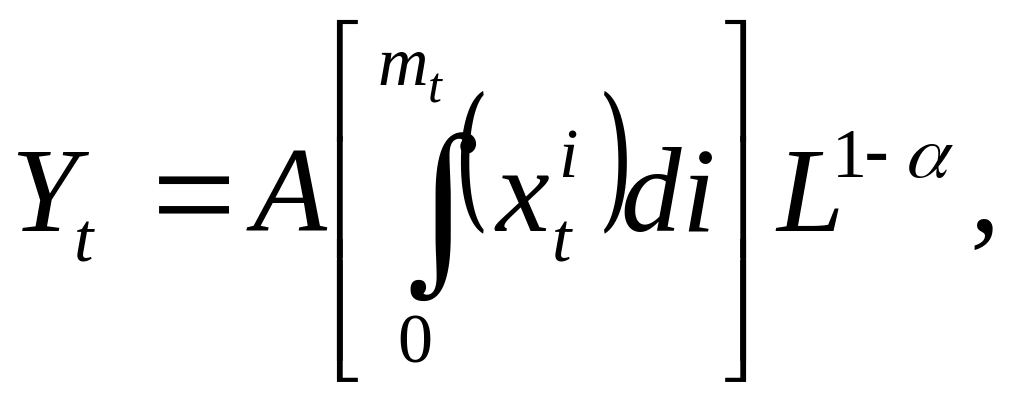0 < α < 1. (2.9.1)

Предположим, что все промежуточные продукты импортируются, и, для простоты, по одинаковой цене p. Тогда задача оптимизации сводится к следующей:

(2.9.2)

Решение (2.9.2) аналогично полученному ранее: .

Если подставить это решение в (2.9.1), то производственная функция примет вид

, где

Допустим, что количество уже введённых товаров . Пусть для того, чтобы ввести новый товар в процесс производства, надо обучить работников его использованию. Издержки обучения каждого работника равны φ, тогда

I_t = (m_{t + 1} - m_t) φL

и, следовательно,

, (2.9.3)

где I_t – инвестиции, связанные с заимствованием новых технологий.

Если сберегается постоянная часть выпуска s, то I_t = s Y_t и с учётом (2.9.3) темп роста выпуска будет

. (2.9.4)

Поскольку издержки заимствования технологий пропорциональны количеству работников, в этой модели размер экономики уже не влияет на экономический рост. Импортные цены, являющиеся для рассматриваемой экономики экзогенным фактором, оказывают влияние на темпы роста. При прочих равных условиях их увеличение снижает темпы экономического роста. Поскольку цены на импорт отражают условия торговли, отсюда следует, что укрепление национальной валюты ведёт к увеличению темпов роста выпуска. Для России это означает, что повышение реального курса рубля может способствовать ускорению экономического роста.

Все модели, пытающиеся объяснить научно-технический прогресс, не объясняют ни абсолютной, ни условной конвергенции. Интересная идея была предложена на этот счёт Ф. Агийоном. Он предложил ввести в модель заимствования технологий ограничение на уровень технологии в каждый момент времени. Темпы роста падают при заимствовании технологий и приближении тем самым бедных стран к границе производственных возможностей, заданной уровнем технологии страны-лидера. Таким образом, появляется возможность в рамках этой модели получить условную конвергенцию.

Преимущество описанных моделей состоит в том, что они выделяют новые детерминанты роста, связанные с решениями фирм по поводу нововведений. Это – издержки, связанные с производством единицы промежуточного продукта, издержки ресурсов в процессе исследований и разработок по созданию нового продукта, издержки обучения работника использованию в процессе производства нового товара, цены на импортируемые промежуточные продукты.

Выводы. Одной из первых теорий роста была теория Харрода – Домара, согласно которой темп роста валового продукта (и национального дохода) находится в прямой зависимости от нормы сбережений и в обратной – от коэффициента капиталоёмкости. Следовательно, темпы роста национальных сбережений определяют в конечном итоге и объемы инвестиций в национальную экономику, и темпы экономического роста. Недостаток внутренних сбережений («дефицит финансирования») может быть компенсирован внешними заимствованиями или помощью со стороны более развитых стран. Развитием этой модели является модель экономического роста с двумя дефицитами.

В неоклассической модели экономического роста Р. Солоу стабильный динамический процесс роста обеспечивается капиталовооружённостью труда. Последняя прямо зависит от нормы сбережений: чем она выше, тем больший запас капитала и более высокий уровень производства. Другие источники экономического роста согласно этой модели: рост населения и технологический прогресс. Причем устойчивый темп роста обеспечивает именно технологический прогресс.

«Новые теории роста» доказывают, что устойчивый экономический рост возможен лишь как эндогенный рост, то есть основанный на увеличении человеческого капитала, которым располагает страна. Низкое качество физического капитала или его относительный недостаток может быть компенсировано инвестициями в человеческий капитал

Контрольные вопросы

1. Что позволяет относить модель Харрода – Домара к числу кейнсианских моделей роста?

2. Что должны были предпринять развивающиеся страны согласно модели Харрода – Домара, чтобы обеспечить экономический рост?

3. Что отличает кейнсианские и неоклассические модели роста?

4. Чем различаются гипотезы строгой и нестрогой сходимости, вытекающие из модели Солоу?

5. Какие практические рекомендации для развивающихся стран следовали из моделей с учётом человеческого капитала?