Задание к работе

1. Методом Крамера найти решение системы линейных алгебраических уравнений.

2. Установить, что система уравнений имеет единственное решение, и найти его с помощью обратной матрицы.

3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений.

4. Интерполяционный полином Лагранжа

Образец решения варианта.

1. Методом Крамера найти решение системы линейных алгебраических уравнений

.

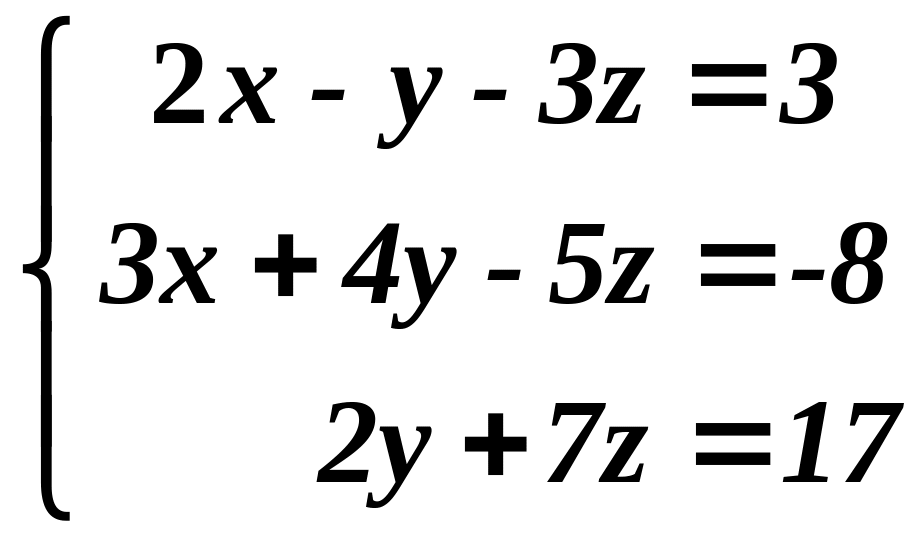Решение.

Решение системы находим по формулам Крамера

.

Вычислим определитель системы

.

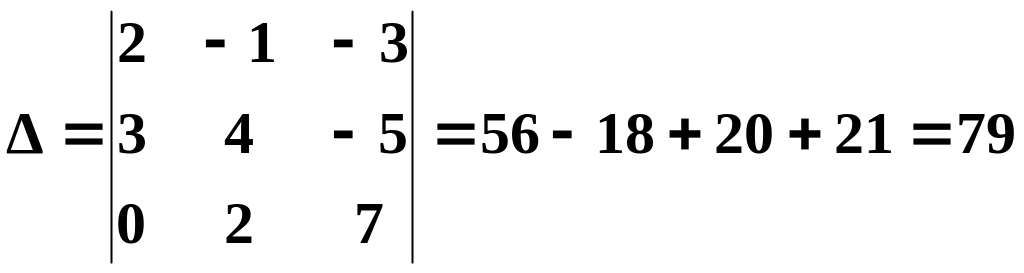Последовательно заменив в , первый, второй и третий столбцы столбцом свободных членов, получим соответственно

;

;

.

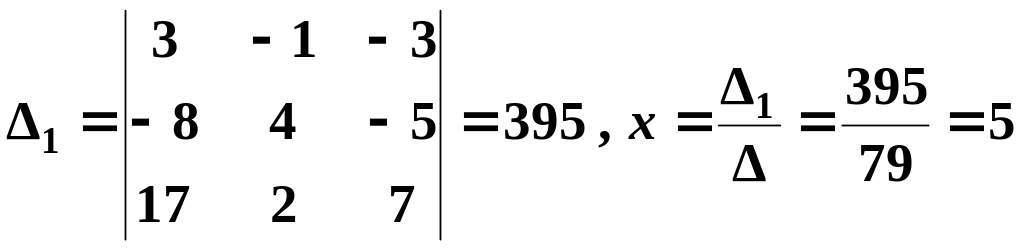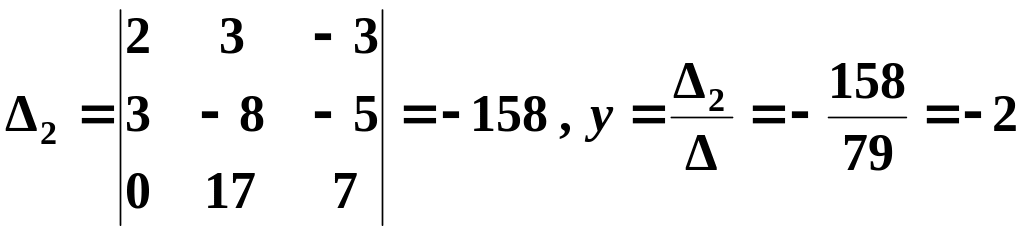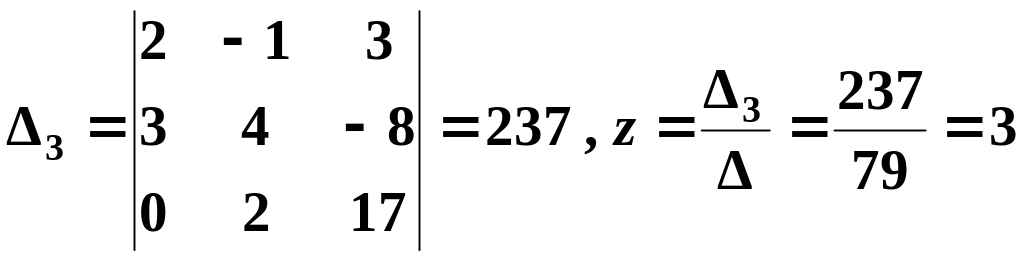Ответ : .

2. Дана система из трех уравнений с тремя неизвестными. Установить, что система уравнений имеет единственное решение и найти его с помощью обратной матрицы

.

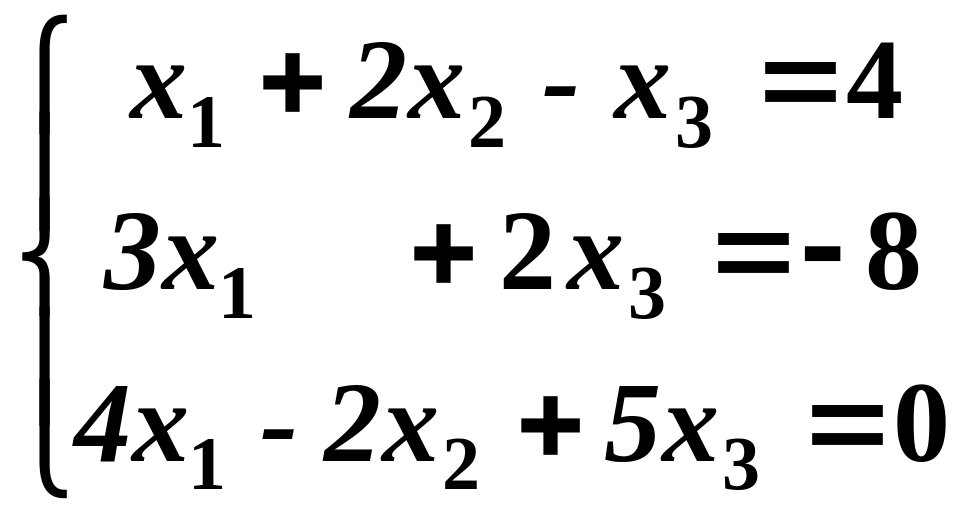Решение.

Если определитель системы отличен от нуля, то система имеет единственное решение (теорема Крамера).

Вычислим определитель данной системы :

,

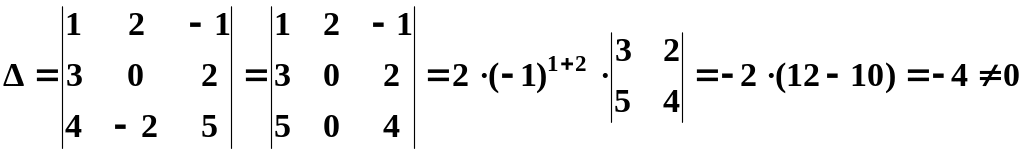следовательно, система имеет единственное решение.

Данную систему можно записать в матричной форме :

, где , , .

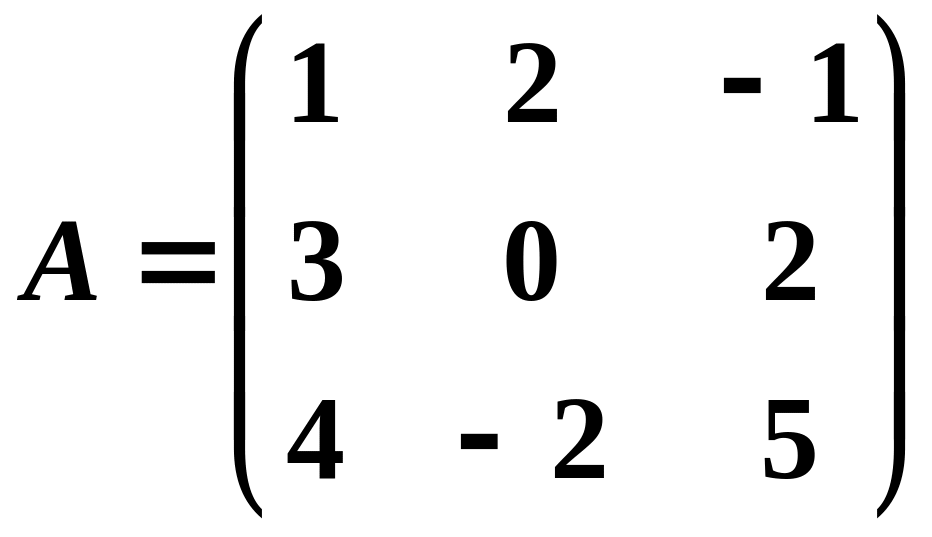Так как , то для матрицы существует обратная матрица . Умножив матричное уравнение слева на , получим , откуда , или .

Найдем обратную матрицу по формуле

,

где алгебраическое дополнение элемента .

,

,

.

.

Тогда

.

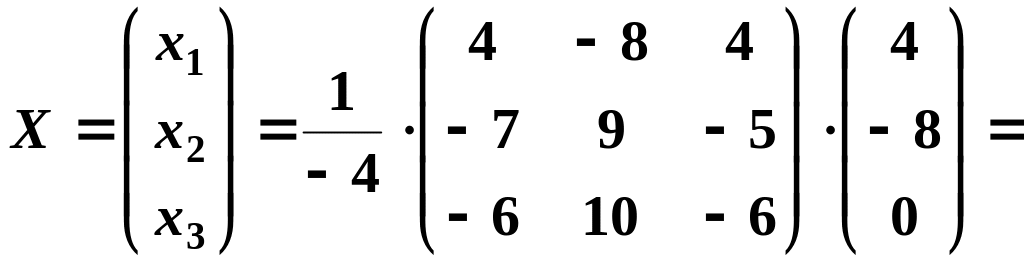
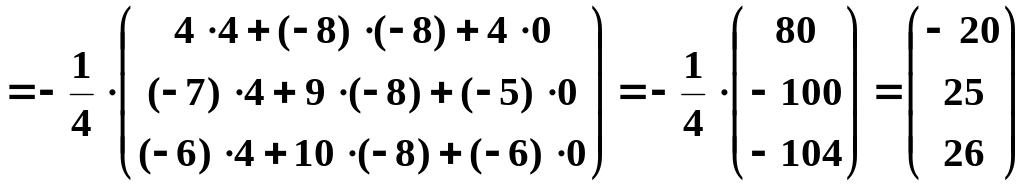Ответ : .

3. Методом Гаусса (или методом исключения неизвестных) найти решение системы линейных алгебраических уравнений

.

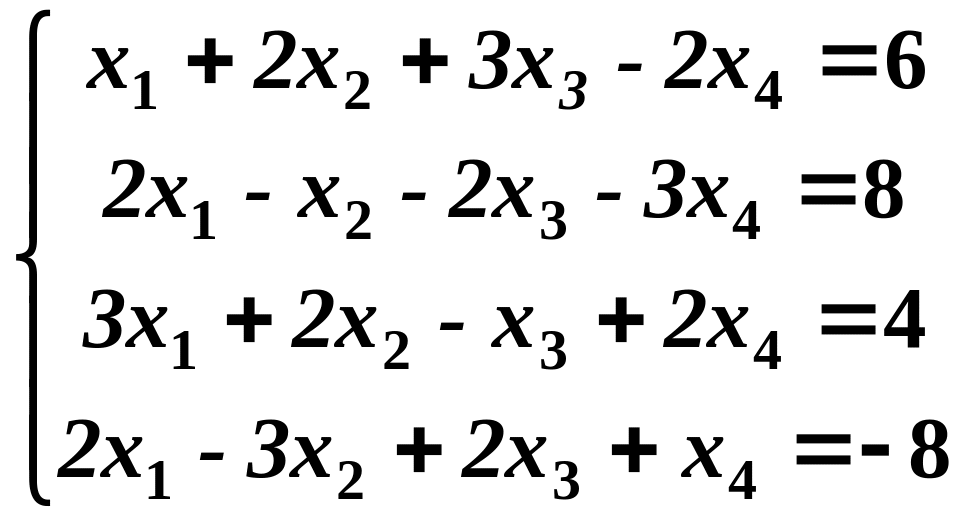Решение.

Выпишем расширенную матрицу данной системы и приведем ее к ступенчатому виду

.

Последовательно умножим первую строку на (–2) и прибавим ее ко второй строке, затем умножим на (–3) и прибавим к третьей строке, умножим на (–2) и прибавим к четвертой строке, получим

.

Ко второй строке полученной матрицы прибавим третью строку, умноженную на , затем во вновь полученной матрице умножим третью строку на , четвертую – на (–1), затем последовательно умножим вторую строку на 2 и прибавим ее к третьей строке, умножим на 7 и прибавим к четвертой строке, получим

.

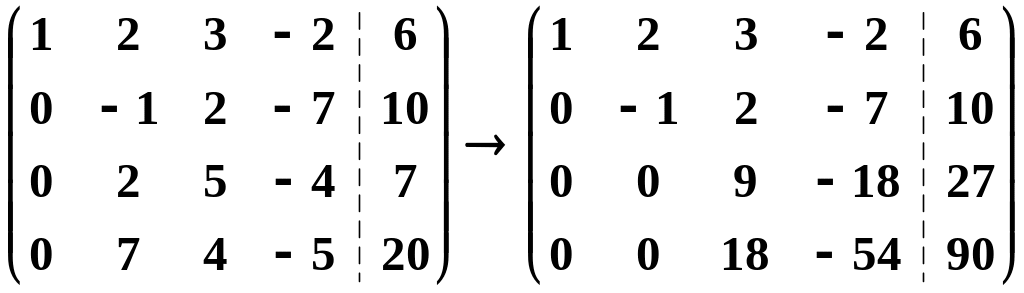Третью строку полученной матрицы умножим на , четвертую – на , затем третью строку умножим на (–1) и прибавим к четвертой строке, получим

.

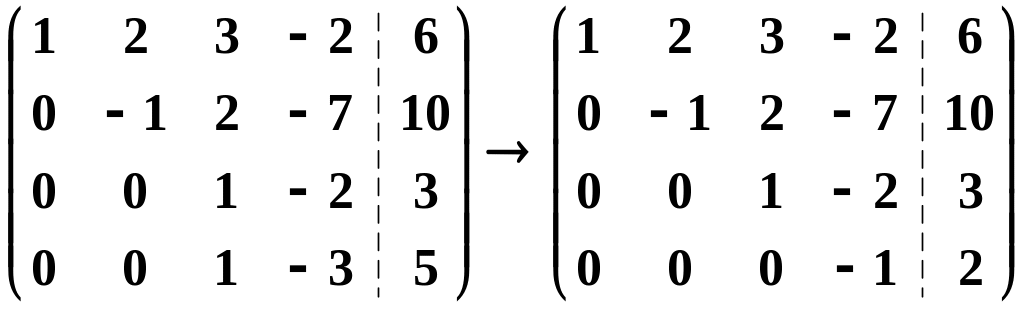Найденная матрица имеет треугольный вид; по этой матрице запишем систему уравнений, эквивалентную исходной системе,

.

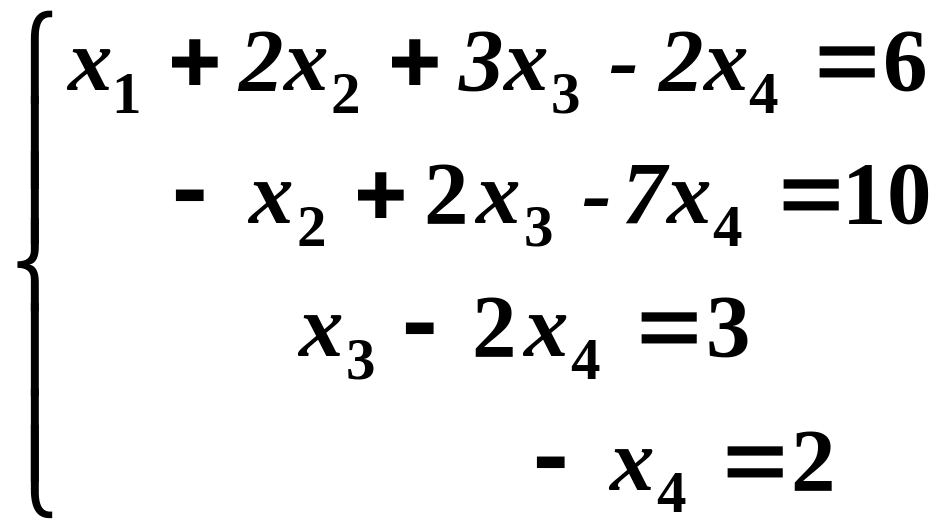Последовательно находим неизвестные, начиная с последнего уравнения, ; подставим в третье уравнение найденное , вычислим , ; затем из второго уравнения находим , ; из первого уравнения получим , .

Ответ : .

4. Построить интерполяционный полином Лагранжа для функции , значение которого приведено в таблице.

	0	1	2	3
	0	0,1	0,3	0,5
	-0,5	0	0,2	1

Интерполяционный полином Лагранжа записывается в виде:

В нашем случае . Рассчитываем полином:

Необходимый многочлен будет иметь вид:

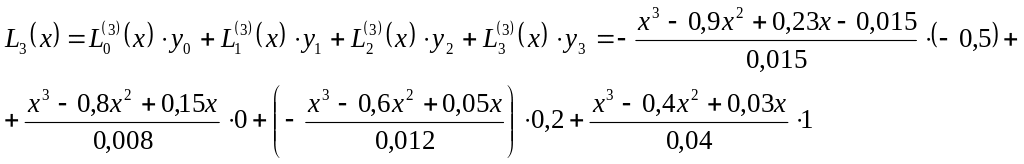
Ответ :

Индивидуальные задания