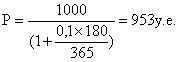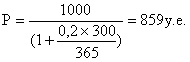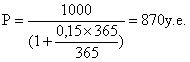Цена и доходность облигации Цена облигаций
Номинальная цена – та величина в денежных единицах, которая обозначена на облигациях.
Эмиссионная цена – та цена, по которой происходит продажа облигаций их первым владельцам. (м.б. равна, больше или меньше номинала).
Цена погашения, та цена, которая выплачивается владельцам облигации по окончанию срока займа.
Часто цена погашения равна номиналу, но может и отличаться.
Курсовая цена – цена, по которой облигации продаются на вторичном рынке.
Теоретическая стоимость: чтобы определить сколько должна стоить данная ЦБ, необходимо найти приведённую стоимость всех доходов.
Приведённая текущая стоимость:
FV- будущая стоимость
R – ставка дисконтирования
N – число лет
В зависимости от способа выплаты процентного дохода 2 типа облигаций
1) с периодической выплатой % дохода – купонная облигация
2) бескупонная (дисконтная) – доход за счет разницы между ценой погашения и эмиссионной ценой.
Купонная облигация
Ставка дисконтирования неизменна
Продается облигация номиналом 1000, купонная ставка 15%, выплата % 1 раз в год. До погашения остаётся 5 лет. Требуемая норма доходности – 20%. Определить расчетную курсовую цену облигации:
Таким образом, искомая цена облигации будет равна:
125+104,17+86,8+72,34+462,16=850,47
В процентном выражении: 85,05%
Формула может быть представлена в виде
P – цена облигации
D – купонный доход в денежных единицах
R – требуемая норма прибыли
или
где
или:
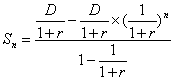
Формула для определения стоимости облигации принимает вид:
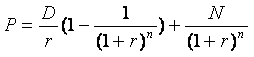
Для приведённого выше примера цена облигации выглядит так:
Ставка дисконтирования меняется из года в год
Если ставка дисконтирования меняется, то надо найти продисконтированные денежные потоки для каждого года.
Формула такая:
- приведённая
стоимость дохода i-ого
года
- доход i-ого
года
r – ставка дисконтирования
Пример:
Продается облигация номиналом 1000, купонная ставка 15%, выплата % 1 раз в год. До погашения остаётся 5 лет. Требуемая норма: в течении первых 3-х лет 20%, 4-й 15%, 5-й 10%. Определить курсовую цену облигации.
Определим приведённую стоимость для платежей каждого года.
1-й год =
2-й год =
3-й год =
4-й год =
5-й год =
P = 917,56
Процентный доход может выплачиваться несколько раз в год
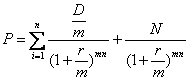
m – число выплат % дохода в течении года
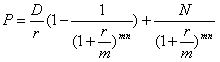
Пример:
Продается облигация номиналом 1000, купонная ставка 15%, выплата % 2 раза в год. До погашения остаётся 5 лет. Требуемая норма доходности – 20%. Определить расчетную курсовую цену облигации:
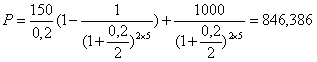
Процентный доход, когда облигация на неполное количество лет
Если, когда срок на целый год, допустим 300 дней, 65 дней в руках продавца. Определить % доход покупателя и продавца.
Формула:
D - процентный доход за год или купонный период
Т – время, в течение которого облигация находилась в руках продавца или покупателя
Dt – процентный доход за время Т
Пример:
Доход покупателя:
Доход продавца:
Доход продавца получит покупатель, то цена облигации такая, чтобы продавец не понес ущерба. (тогда к цене 850 надо добавить 26,71)
Тогда Р = 850,429+26,71≈877.
(850 – это за 5 лет, что бы было более точно, то надо продисконтировать тот доход, который остался до погашения облигации)
Формула справедливой стоимости для нецелого числа лет:
Где k=T/365
N – целое число лет, включая нецелый год.
Т – число дней до выплаты первого купона.
Определить цену облигации для нашего примера:
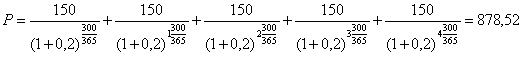
Облигации с переменным купоном
Купонные облигации могут быть с переменной купонной ставкой, т.е. величина % дохода изменяется в зависимости от ситуации на финансовом рынке. Пример – облигация государственного сберегательного займа (ОГСЗ), облигация федерального займа с переменным купоном (ОФЗ-ПК).
Формула:
D1,2…n - процентный доход для каждого периода
R1,2…n – требуемая норма прибыли (ставка дисконтирования), ставка дисконтирования.
Пример:
Номинал – 1000, до погашения 3 года, % доход 2 раза в год, по первому купону – 20%, определить курсовую цену облигации.
Инвестор пришёл к выводу, что купонная ставка по облигации будет снижаться: 1-й год 20%, 2-й 18%, 3-й 15%, соответственно будет снижаться и требуемая норма прибыли по данному типу облигации: 1-й год 20%, 2-й 19%, 3-й 16%.
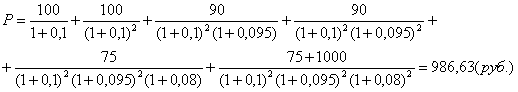
Бескупонная облигация
Цена бескупонной облигации может представляться, как купон облигации с нулевым размером купонных платежей (не правда ли, адский облом?).
.
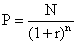Пример:
N= 1000 у.е.
n = 4 года
Определить курсовую цену, если ставка дисконтирования r = 14%
Друзья, давайте представим, что погашение через 3 года 180 дней.
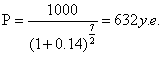
Эта формула может быть использована для цены краткосрочных ценных бумаг (депозитарных сертификатов). Пример:
Определить курсовую стоимость облигации за срок 180 дней. Требуемая норма прибыли = 20% годовых
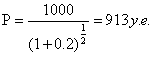
Но для определения цены краткосрочной облигации обычно используется другая формула:
,
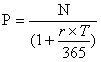где Т = количество дней через которые
гасим (наглухо) облигацию.
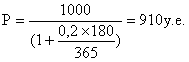
910 < 913, поэтому непонятно. Рассмотрим еще пример:
r=10%
N=1000
T=180 дней
Не врубились? Не вопрос, вот вам еще примерчег:
r=20%
N=1000
T=300 дней
Опять не воткнули? Как с вами сложно! Ладно, еще пример:
r=15%
N=1000
T=365 дней
Вот теперь врубайтесь, чуваки и чувихи, расхождение должно быть тем меньше, чем меньше r и чем больше срок до погашения облигации. Т.к. расхождения незначительны, то обычно используют вторую формулу.
Вы уже подросли. Пришло время поговорить с вами об этом!
Об определении доходности облигаций.