
- •А. Б. Климовский
- •Часть 2
- •Vqsin а
- •Мы получили линейное дифференциальное уравнение. Проинтегрируем его, за-
- •Будем считать, что электрон в атоме движется со
- •Теорема Гаусса для магнитного поля.
- •Магнитные волны отличаются друг от друга по способам создания и регистрации, а также по своим свойствам. Электромагнитные волны условно делят на несколько
- •Зеркала Френеля (1816 г.)
- •Бипризма Френеля
- •3. Билинза Бийе
- •Называют оптическои разностью хода .
- •Разности хода
- •X, или, что для интерференции то же самое, ниче-
- •Тема: Дифракция волн
- •1788-1827) И получил название принципа Гюйгенса-Френеля. Он состоит из нескольких основных положений: первичной волны
- •Если часть поверхности закрыта непрозрачным экраном, то закрытые участки не излучают, а открытые излучают так же, как если бы не было экрана.
- •Тема: Взаимодействие электромагнитных волн с веществом
- •В некоторых диапазонах длин волн k наблюдается
- •Для испускательной способности используют два выражения -
- •4,965 (Точного решения не существует). Таким образо
- •Кинетическая энергия вылетевших электронов должна зависеть от интенсивности света
- •Кинетическая энергия электронов не должна зависеть от частоты света.
- •Теперь найдем длину волны де Бройля для микрообъекта, в качестве которого
- •Функция ¥ должна быть конечной, непрерывной и однозначной;
- •Производные ——, ——, ——, -г— должны существовать и быть
- •Квадрат модуля функции № должен быть интегрируем, то есть интеграл
- •В котором разделены переменные - у является функцией координат, ф - функцией
- •Контрольные работы
- •Список лабораторных работ Электромагнетизм
- •Колебания. Волны. Оптика
- •Квантовая и атомная физика
- •Список дополнительной литературы
- •Единицы физических величин
- •Оглавление
- •Содержание остальных частей курса лекций
- •Часть 1
- •Часть 3
- •Электрические свойства полупроводников и полупроводниковые приборы
Называют оптическои разностью хода .
Е
Ar
=
L2
-
L1
Разности хода
В общем случае
2л , ч |
|
|
2п . |
Ф2 -Ф1 =— (n2L2 - n1L1) |
или |
Аф = |
ТА |
Если П1 Ф const и П2 Ф const, то оптическая разность хода находится интегрированием А = J П2dl - J Uidl. Здесь первый интеграл берется по пути второй волны в
своей среде, а второй - по пути первой волны в своей среде.
Условия максимумов и минимумов можно записать для оптической разности хо-
2п 2п
да, так как АФ = - А, то при А = 2тп получаем
X
X
А
условие максимумов
= тХ = 2т Х 2
о
- оптическая разность хода равна целому числу длин волн или четному числу полуволн. Соответственно,
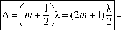
условие минимумов
птическая разность хода равна полуцелому числу длин волн или нечетному числу полуволн.
Почему же мы не наблюдаем интерференции света, например, от двух ламп. Дело в том, что все естественные источники дают некогерентный свет. Более того, абсолютно когерентных источников не существует. Это идеализация. В реальных случаях более уместно говорить о степени когерентности света.
Для определения степени когерентности рассматривают по отдельности пространственную когерентность, для количественного описания которой используют рког - радиус когерентности, и временную когерентность, для
описания которой используют т ког - время когерентности и Ьког = ctког - длину когерентности.
Рассмотрим сначала пространственную когерентность.
Если свет монохроматичен, тогда в идеальном случае точечного источника на экране будет наблюдаться устойчивая интерференционная картина. Увеличение размеров источника приводит к ухудшению ее контрастности и к полному исчезновению. Это связано с тем, что максимумы интерференционных картин точечных источников части протяженного источника наложатся на минимумы интерференционных картин точечных источников другой части протяженного источника, и общая интерференционная картина исчезнет. Для получения интерференционной картины необходимо, чтобы размер каждого источника не превосходил определенного предела, зависящего от взаимного расположения источников и расстояния между ними, а также положения экрана. Источники называются пространственно когерентными, если их размеры и положения позволяют наблюдать интерференцию.
Если
волны от крайних точек S
и
S'
протяженного источника выходят
симметрично для некоторой точки
экрана P,
и а - угловой размер источника, то
условие
хорошей контрастности
для
этого источника будет иметь вид
, . а X l sin— < — 2 2 |
, или |
1 < X |
— < ~ • а 2sin2 |
||
|
|
П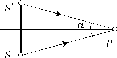 од
радиусом
когерентности понимают
минимальное
расстояние между двумя точками
протяженного источника, расположенными
на плоскости, перпендикулярной к
направлению распространения волны, при
котором интерференционная картина
от световых волн, излучаемых этими
точечными источниками, исчезает. Для
источника, размеры которого равны
радиусу когерентности,
интерференционные картины от двух
половин источника, накладываясь, дают
равномерную освещенность экрана.
од
радиусом
когерентности понимают
минимальное
расстояние между двумя точками
протяженного источника, расположенными
на плоскости, перпендикулярной к
направлению распространения волны, при
котором интерференционная картина
от световых волн, излучаемых этими
точечными источниками, исчезает. Для
источника, размеры которого равны
радиусу когерентности,
интерференционные картины от двух
половин источника, накладываясь, дают
равномерную освещенность экрана.
Радиус
когерентности определяется из условия
исчезновения интерференционной картины
при l
=
р ког.
Тогда радиус когерентности можно
выразить через угловой раз-
X . а а
мер
источника р
ког
= .
При малых углах sin
—
»
—,
следовательно,
_ . а 22
ш 2
X
р
а
ког
Радиус
когерентности обратно пропорционален
угловому размеру источника из точки
наблюдения, чем меньше а, тем больше
радиус когерентности.
Для
строго плоских
идеальных волн (излучаемых
бесконечно удаленным источником)
все направления лучей параллельны, а =
0, и они пространственно
абсо-
X
лютно
когерентны
рког
=
— = да . Для реальных источников (не
бесконечно удаленных) пространственная
когерентность повышается (растет р
ког)
по мере удаления от
источника.
Например, свет звезд обладает высокой
степенью когерентности. Высокой
пространственной когерентностью
обладает излучение лазеров, световые
лучи которых характеризуются высокой
направленностью.
В
классическом опыте
Юнга (T.
Young, 1773-1829)
источником света S
служила
освещенная узкая щель угловым размером
а» 5 • 10 4
рад.
За щелью S
на
расстоянии d
друг
от друга были расположены две щели Si
и
S2
. Для наблюдения ин-
X
терференции
должно выполняться условие d
<
р
ког
=
—. Чтобы выполнить это условие для
средней длины волны излучения X = 550 нм,
Юнг
расположил щели Si
и
S2
,
X 5,5 • 10-7
.
на
расстоянии d
<
— = — » 1 мм
,
и ему удалось наблюдать интерференцион-
а
5 • 10-4
ную
картину.
л X
При
d
>
— интерференционная
картина пропадает. Опыт, аналогичный
опыту а
Юнга,
за 150 лет до него был осуществлен в 1665
году Франческо Гримальди (F.
Grimaldi, 1618-1683).
В опыте Гримальди первой щели S
не
было, и свет падал прямо от Солнца.
Угловой размер Солнца а
* 30” = 0,0087рад,
тогда для получения интерференционной
картины было необходимо, чтобы щели Sj
и
S2
находились на расстоя-
X
нии
d
<
— * 6
•
10
нм
=
0,06
мм
.
Это условие в опыте Гримальди не было
выполне- а
но,
и интерференционную картину Гримальди
получить не удалось.
Перейдем к рассмотрению временндй когерентности.
Мы
рассматривали строго
монохроматические волны одной и той же
частоты. Такие
волны, излучаемые идеальными (точечными)
источниками, когерентны, то есть всегда
интерферируют. Интерференционная
картина таких источников устойчива,
распределение интенсивности на
экране неизменно во времени.
И_8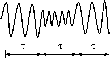 злучение
реальных источников не является строго
монохроматичным и, если они независимы,
то усиление и ослабление светового
потока при их наложении недоступны
наблюдению. Поясним это на модели
идеализированных источников, излучающих
почти монохроматические волны, амплитуда
и фаза которых хаотически изменяется
за время, много большее периода колебаний.
Такая волна представляет собой
совокупность «обрывков» гармонических
волн разной амплитуды и фазы. Примером
может служить излучение изолированного
атома, который в
злучение
реальных источников не является строго
монохроматичным и, если они независимы,
то усиление и ослабление светового
потока при их наложении недоступны
наблюдению. Поясним это на модели
идеализированных источников, излучающих
почти монохроматические волны, амплитуда
и фаза которых хаотически изменяется
за время, много большее периода колебаний.
Такая волна представляет собой
совокупность «обрывков» гармонических
волн разной амплитуды и фазы. Примером
может служить излучение изолированного
атома, который в
течение
т * 10 _ с
испускает
ряд волн или, как принято говорить,
цуг волн,
независимо следующих друг за другом.
При наложении света цугов двух атомов
на экране получится некоторая
интерференционная картина, которая
определяется разностью фаз между
колебаниями обоих цугов. За одну секунду
сотни миллионов раз сменятся пары цугов,
хаотически изменится разность фаз, и
столько же интерференционных картинок
промелькнет на экране. Глаз или другой
приемник света не в состоянии уследить
за этой сменой картин и фиксирует только
равномерную освещенность экрана.
Рассмотрим
идеализированный немонохроматический
источник. Допустим, что свет источника
S
представляет
волны с длинами волн из диапазона (X, X
+ 5X).
Если
.vл,8X
для
некоторой точки экрана разность хода
для волн с длинами волн X и X = X +
б
[N+i
V 2 У
X, то волны с длиной волны X'
удет определяться выражением Д = NX'
придут
в эту точку в фазе, а с длиной волны X
- в противофазе. В этом случае макси-
8
X, X + —
V 2 у
XЛ
мумы
интерференционных картин диапазона
наложатся
на минимумы ин-
X + , X + 8X
V 2’ ,
и интерференционные полосы
X
или
терференционных
картин диапазона исчезнут. Условие
исчезновения полос
будет NX'
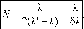
Максимумы и минимумы с номерами, меньшим, чем N, будут видны, а с номером порядка N и более будут смазаны. Это означает, что квазимонохроматические волны, когерентные при низких порядках интерференции, перестают быть когерентными при высоких порядках N ~ -=т-.
OX
Нарушение когерентности в данном случае связано с запаздыванием одних волн по сравнению с другими. Поэтому и говорят о временндй когерентности, количественной характеристикой которой является Тког - время запаздывания между волнами, при котором интерференционная картина пропадает, которое называют временем когерентности . За время когерентности волна проходит расстояние, равное длине когерентности.
Длиной когерентности называется минимальная разность хода между двумя волнами вдоль направления распространения волны, при которой интерференционная картина пропадает, и волны нельзя считать когерентными. По определению Lког - разность хода между волнами, при которой пропадает интерференционная кар-

тина, таким образом
Тогда время когерентности
,
где V
- фазовая скорость волны.
_
1
VOX
П
Тког Ov
оскольку частота волны V = —, то OV = ——, и тогдаX X2
Принято считать, что наибольший порядок наблюдаемого максимума интерференции определяется из условия
N
L
ког
.max
Для теплового источника (например, электрической лампочки), испускающего
1
10 _15 с и,
ког
Av
весь
диапазон длин волн Av
=
1015
Гц,
время когерентности, х
1
L
0 _7 м.
к
соответственно
\_7
X ~10_■ м максимальный порядок Nmax < 1 , и интерференционная картина не наблюдается.
Для лазерных источников, генерирующих достаточно монохроматические волны
2 _2 с Av«10 Гц, время когерентности хког = 10 с, и длина когерентности
LK02
*
10 м.
В принципе, используя лазерные источники,
можно наблюдать интерференцию с
разностью хода в несколько километров,
но в реальности при большой разности
хода сказываются неоднородность земной
атмосферы и трудности создания стабильного
интерференционного устройства таких
размеров.
После
обсуждения понятия когерентности света
перейдем непосредственно к рассмотрению
интерференции, и далее всегда будем
считать волны когерентными, то есть
расстояние между источниками будем
считать меньше радиуса когерентности,
а разность хода меньше длины
когерентности. При необходимости будем
указывать условия, обязательные для
выполнения этих требований.
Самый
простой случай интерференции - образование
стоячей
волны,
являющейся результатом
наложения распространяющихся навстречу
друг другу бегущих волн
(часто это падающая и отраженная от
преграды волны).
Пусть
накладываются две плоские волны,
распространяющиеся вдоль оси Ox,
первая -
в
положительном направлении, вторая -
навстречу,
Ex = E0 cos(rot - kx) и E2 = E0 cos(rot + kx + ф).
г
ФЛ
kx
+ —
Ф
rot + —
V 2 у
Суммарная
волна Е
= Е} + Е2
= 2Eo^S
cos
является
с
Ф
rot + —
V 2 у
с ампли-
тоячей волной
Ф
2
тудой A( x) = 2Eo cos
kx
+
зависящей от координаты х точки стоячей волны.
Т
Пучности
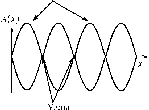
или
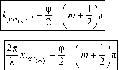
Расстояние
между узлами
Ат = х - х = —
узл Хузл (т+1) Хузл(т) 2 .
Точки,
в которых амплитуда стоячей волны
максимальна, A(x)
=
max
=
2E0,
называются пуч
н о с т я м и,
их положение определяется условием
2п ф
X ХпуЧ (т) + = тП
i Ф
kx«>4
(m)
+
2 = тП
. Расстояние между пучностями также,
или
к
Ах
пуч
ак и для узлов равно половине длины волны,
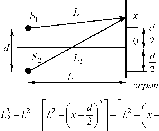
Для
стоячих
электромагнитных волн
положения пучностей напряженности
электрического
поля E
совпадает
с узлами индукции магнитного поля B,
и наоборот. Это позволяет разделить
магнитное и электрическое поле в стоячей
волне. Получение стоячих
электромагнитных волн
сопряжено с трудностями, связанными с
малостью длины волны. Кроме того,
необходимо, чтобы между областью
интерференции и отражающей поверхностью
было расстояние меньше длины когерентности
LKtог
.
Получение
стоячих
звуковых волн
с частотами, например, около V
= 1 кГц,
не вызывает никаких проблем. Скорость
звука в воздухе приблизительно равна
V
* 330 м/с
(точное значение зависит от температуры
воздуха). Нестабильность частоты
может быть легко достигнута порядка
Sv
*
10 Гц.
Следовательно, для этих волн
X
= 33 см,
а LKOB
=
Vt0
=
V
— = 33 м.
Наблюдение пучностей (и узлов), расстоя-
Sv
ние
между которыми А/ * 15 см,
в столбе воздуха длиной 1 м не представляет
экспериментальных трудностей.
Заметим, что стоячая волна в отличие от бегущей волны не переносит энергию. Можно сказать, что падающая волна переносит энергию в одну сторону, а отраженная навстречу, в результате энергия не переносится. Для стоячих электромагнитных волн энергия, не распространяясь, колеблется, переходя из энергии магнитного поля в энергию электрического поля и обратно.
Перейдем к подробному рассмотрению другого примера интерференции (уже неоднократно упоминавшемуся опыту Юнга).
Найдем положение точек экрана, соответствующих максимумам или минимумам (светлым и темным областям). Для этого нужно найти разность хода А = L2 — L1 для
произвольной
точки с координатой X,
где
L1
-
путь, проходимый светом до точки х
от
источника S1,
L2
-
от источника S
2.
Сначала
найдем разность квадратов
Л2 f
лЛ2
т2
7-2
и
L1
=
L
+
Тогда
(L2
— L1
)(L2
+ L1)
= (L2
— L:
) = 2xd.
В
опыте Юнга расстояние d
между
источниками мало (для пространственной
когерентности), x
мало
(для временной когерентности), то есть
d
<<
L
и
x
<<
L.
При
2
* L
и
L
+
l2
этом
можно считать, что L1
*
L
*
L
и
L
+
L
*
2L.
Тогда
получаем А • 2L
=
2xd,
и разность хода
\2
d
X
Н V 2У
d
x 2,
2
l22
=
LL
+
4
4
xd
А=т
Соответственно, используя условие максимумов интерференции Л = mk и усло-
Г 1 ^
ш
вие минимумов интерференции Л
+ — k,2
получаем для максимумов
V
V
1
k. Тогда их координаты
ш
+
—
2 /
L
xmaxd
„.л xmind
=
Шк,
и
минимумов
L
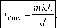
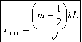
d
d
Расстояние между максимумами
^max = xmax(m+1) _ xmax(ш) Расстояние между минимумами
(ш + 1)kL mkL kL = d'
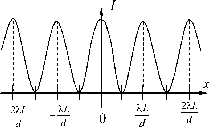
kL
^min xmin( m+1) xmin( m)
Распреде-
полос
ление интенсивности света представлено на рисунке.
Заметим, что условия максимумов и минимумов зависят от длины волны, следовательно, если свет не монохроматический (содержит
волны разной длины волны), то для каждой волны получится своя картина интерференции. Полосы для различных длин волн будут иметь разную толщину и будут находиться на разном расстоянии друг от друга (в зависимости от длины волны).
Перейдем к следующему примеру интерференции - интерференция в тонких пленках.
Пусть
тонкая пленка толщиной d
с
оптической плотностью n
находится
в воздухе, и под углом i
на
пленку падает пучок монохроматического
света.
Для
тонких пленок, если d
<
LKoa,
будет наблюдаться интерференция волн
(лучей), отраженных от передней и задней
поверхностей пленки. Результат
интерференции определяется разностью
фаз 1' -го и 2'
-го лучей.
Если свет белый, то, как мы получили ранее, LKoa * к, тогда для наблюдения интерференции толщина пленки d должна быть d < LKoa * k. При этом, если d << к,
^ _ kL
d d
Таким образом, светлые и темные области при использовании щелей в качестве источников будут представлять собой полосы, равноотстоящие друг от друга, при этом середина светлой полосы бу-
дет расположена строго меж- ду темными, а середина тем- ной полосы строго посереди- не между светлыми. Ширина
kL
Лх =
d
(m +1) +
то, как мы увидим, будет наблюдаться только центральный минимум, и пленка в отраженном свете становится темной.
Рассмотрим монохроматическую волну с длиной волны k . Найдем разность хода А лучей 1 — 1' и 2 — 2'.
Д о
отрезка АВ
волны
1
и
2
пройдут
одинаковый путь. И от точки D
волны
1' и 2'
пройдут одинаковый путь. Точки отражения
луча 2
и
выхода луча 1
совпадают,
хотя на рисунке они для
наглядности разнесены. Тогда
о
отрезка АВ
волны
1
и
2
пройдут
одинаковый путь. И от точки D
волны
1' и 2'
пройдут одинаковый путь. Точки отражения
луча 2
и
выхода луча 1
совпадают,
хотя на рисунке они для
наглядности разнесены. Тогда
А = n( AE + ED) — BD.
d
Из рисунка
AE
=
ED
=
cos у
BD = ADsin r, где y - угол преломления, r - угол отражения. Так как AD = 2AC, AC = d • tgY, r = i, то разность хода будет равна
2nd _ , . . 2nd 2nd • sin y . ~ , А = 2d • tgy • sin i = sin y = 2nd • cos y .
cosy cosy cosy
Воспользовавшись законом преломления sin i = n • sin y , получим
А = 2nd • cosy = 2nd-/1 — sin2 y = 2dVn2 — sin2i.
Окончательное выражение для оптической разности хода получим, если учтем скачкообразное изменение фазы на К при отражении луча от более плотной среды -
Аф = + п или А = +—. Тогда оптическая разность хода будет равна
2
А = 2d-/
• 2 • , k n — sin i + — 2Заметим, что здесь законы отражения, преломления и изменения фазы волны при отражении мы использовали без обоснования, поскольку все эти законы мы рассмотрим, когда будем изучать взаимодействие света с веществом.
Запишем условия максимумов и минимумов интерференции в тонких пленках (m - целое число).
Условие максимумов
2dVn2 — sin2 i =
k
—
m
+-
v 2
или
2dVn2 — sin2 i + — = mk
Условие минимумов
k
2d/
2dy/n2 — sin2 i = mk
или
9 .9 # V # V
n — sin i + — = mk + —
2 2
k
При этих условиях максимумы и минимумы будут наблюдаться в отраженном от пленки свете.
