• Теорема Гаусса для магнитного поля.

Величины, входящие в левые части уравнений Максвелла, не являются независи­мыми, и между ними существует связь, которая для изотропных несегнетоэлектриче- ских и неферромагнитных сред будет иметь вид

D = 8 ₀sE

где 8 о и ^ о - соответственно электрическая и магнитная постоянные, 8 и ц - соот­ветственно диэлектрическая и магнитная проницаемости, G - удельная проводимость вещества.

Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями.

Если поля не изменяются с течением времени, такие поля называются стацио­нарными полями, то уравнения Максвелла в пустом пространстве (вакууме) примут вид

f DdS = Q;

(S)

(L)

f BdS = 0

(S)

f Edl = 0;

(L)

f Hdl = I;

(L)

Источниками электрического поля в данном случае являются только электриче­ские заряды Q , источниками магнитного - только токи проводимости I . В этом слу­чае электрические и магнитные поля независимы друг от друга, что позволяет изучать отдельно постоянные электрическое и магнитное поля, как мы и поступали до сих пор.

Уравнения Максвелла - наиболее общие уравнения для электриче­ских и магнитных полей в покоящихся средах.

Уравнения Максвелла выражают основные законы электромагнетизма. Они столько же фундаментальны, как три закона движения и закон всемирного тяготения Ньютона в механике.

В некотором смысле уравнения Максвелла даже более фундаментальны, так как в отличие от законов Ньютона они справедливы и в релятивистском случае.

Из уравнений Максвелла следует, что переменное магнитное поле всегда порож­дает электрическое поле, а переменное электрическое поле всегда порождает магнит­ное, то есть электрические и магнитные поля неразрывно связаны друг с другом - они образуют единое электромагнитное поле. Теория Максвелла объединила в одно два взаимодействия - электрическое и магнитное, до того рассматриваемые как отдельные, независимые взаимодействия.

Важным следствием взаимопорождаемости переменных электрических и магнит­ных полей являются электромагнитные волны, существование которых вытекает непо­средственно из уравнений Максвелла.

Тема: Электромагнитные колебания

Вопросы:

1. Уравнения, описывающие электромагнитные колебания в колебательном контуре. Решение.

2. Затухающие колебания в колебательном контуре. Характеристики.

3. Вынужденные колебания в колебательном контуре. Резонанс заряда и тока.

4. Цепи переменного тока. Реактивное сопротивление.

Импеданс (полное сопротивление).

5. Закон Ома и закон Джоуля-Ленца для цепей переменного тока.

6. Эффективное (действующее) значение силы тока и напряжения.

Как мы отметили в предыдущей теме, из уравнения Максвелла непосредственно вытекает существование электромагнитных волн, которые являются распространением в пространстве колебаний электрического и магнитного полей.

Прежде чем перейти к электромагнитным волнам, мы рассмотрим электромаг­нитные колебания. Основные определения для колебательного процесса мы рассмотре­ли в первой части курса, когда говорили о механических колебаниях. В этой теме мы рассмотрим только то, что относится к электромагнитным колебаниям.

Простейшей системой, в которой возникают колебания электрического и магнит­ного поля, является колебательный контур.

К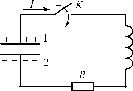

L

олебательный контур - электрическая цепь, состоящая из катушки индуктивностью L, конденсатора емкостью C и резистора сопротивлением R, ис­пользуемая для возбуждения и поддержива­ния электромагнитных колебаний.

Мы рассмотрим последовательный колебательный контур, в котором все эле­менты соединены последовательно.

П

C

о закону Ома для неоднородного участка цепи (1 — L — R — 2) имеем IR = S + ф_х — ф ₂,

где I, Аф = ф2 — фх и S

мгновенные

значения соответственно силы тока в цепи,

разности потенциалов между обкладками 1 и 2 конденсатора и алгебраической суммы ЭДС, приложенных на участке цепи (1 — L — R — 2). На рассматриваемом участке це­пи действует только ЭДС самоиндукции, возникающая в катушке при протекании по ней изменяющегося тока. Поэтому

dI L —, dt

dI

L— — Аф. dt

S

следовательно, IR

Обозначим заряд одной обкладки конденсатора через q. Тогда по определению силы тока

d

_{I =} dq_

и

I d ² q dt

dq dt dt²

Р

^Аф = ф 2 ^— ф1 = ^.

азность потенциалов между обкладками конденсатора равна

C

Подставив полученные выражения в закон Ома, получим дифференциальное уравнение второго порядка вида

или

L^q+R^q+q=о

2

dt C

dt

2

Уравнения такого типа X + 2РХ + ГО₀ x = 0 нам уже встречались в первой части курса физики, когда рассматривали затухающие механические колебания. Его решени­ем при слабом затухании ( в < ГОо ) будет функция

x(t) = Ae ^в sin (rot + а₀ )

где го = V^ю о — в~ - частота затухающих колебаний.

Сравнивая уравнение, полученное для колебательного контура, с уравнением, по­лученным ранее, видим, что для колебательного контура коэффициент затухания

о R 1

в = , и частота гармонических колебаний ГОо = , . Следовательно, решени-

^2L л! LC

ем полученного для колебательного контура дифференциального уравнения будет функция вида

R

1

q(t) = q_me ^2L sin(rot + а_о)

_R2

1

где частота затухающих колебаний в колебательном контуре ГО =

2п

а

LC 4L²

2п

период T =

го

. Начальные фаза а о и амплитуда колебаний q_m

1 R² LC 4L²

зависят от способа возбуждения колебаний, то есть от начальных условий.

Таким образом, при подключении заряженного конденсатора к цепи, состоящей из последовательно соединенных индуктивности и резистора, заряд на обкладках кон­денсатора будет совершать затухающие колебания, если сопротивление резистора не слишком велико (затухание мало).

С увеличением сопротивления R контура период колебаний в нем возрастает, и

при R = 2л/L / C обращается в бесконечность. При R > 2л/L / C решением диффе­ренциального уравнения является апериодическая функция

к = #■—

q = A_xe ~^^te^kt + A₂e ~^pte ~^—k.

ГОг

где

Если сопротивление велико, то в контуре будет происходить апериодический процесс убывания заряда на конденсаторе. Мы далее в этой теме будем говорить только о коле­бательных процессах, то есть будем считать, что затухание мало R < 2л/L / C .

Амплитуда q(t) колебаний заряда q конденсатора экспонен­циально убывает

R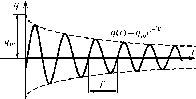

-et

1

q^(t) = qm^{e 2L} = qm^e

Разность потенциалов Дф

между обкладками конденсатора пропорциональна заряду. Поэтому

Сила тока в колебательном контуре

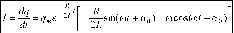
Пусть в начальный момент времени (t = 0) заряд конденсатора q = q$ и ток в цепи отсутствует. Тогда начальные условия будут иметь вид

•

R • п

q_m sm a₀ = q₀, oysma₀ - юcosa₀ = 0,

2L

откуда для начальной фазы a q и начальной амплитуды qo получим следующие выра­жения:

ю

4 L

ю

1

tg a

o

R /2L p

= qoV¹ + ^ctg^{2 a} o = qo

r ²c

qo

qo

1+

^qm

R ²C

~4.L

sm a

o

ю

1-

¹ a ^R - Г~2 r72"_

F7^ P = TT ^{, а ю} V ^ю0 ^- P =

1

r_

LC ’ ^ 2L

Таким образом, начальные фаза и амплитуда колебаний в контуре могут быть вы­ражены через параметры контура: емкости, индуктивности и сопротивления. Причем вид выражений будет разным в зависимости от способа возбуждения колебаний (на­чальных условий).

Если сопротивление R контура уменьшить, то затухание колебаний в нем также уменьшится. В пределе, при R = 0 (в = 0), такой контур называют идеальным колеба­тельным контуром, свободные электромагнитные колебания в контуре становятся не­затухающими. В идеальном колебательном контуре заряд конденсатора, разность по­тенциалов между его обкладками, сила тока в цепи и ЭДС самоиндукции изменяются по гармоническому закону

q

q = qm sin^t + aq) ; Дф = -^msin^t + aq) ;

r ⁰

так как ю

LC 4L²

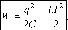
f

п

I = q_mro₀ cos(ro₀t + а₀) = q_mro₀ sin

^ro0^t + ^а0 + 9

V ²

€ = — q_mro0 sin(ro₀t + а₀ ) = q_m<TO_d sin(ro₀t + а₀ + п),

где ГОо = i/4lc - циклическая частота свободных незатухающих электромаг­нитных колебаний в контуре. Период свободных незатухающих колебаний опреде­ляется формулой Томсона (J.-J. Tomson, 1856-1940)

T = (2п / ro₀) = 2W LC

Как видим из записанных выражений, сила тока отстает по фазе от разности по­тенциалов между обкладками конденсатора на П /2 и опережает ЭДС индукции тоже на П /2.

Амплитуда I_m силы тока и амплитуда Aty_m разности потенциалов обкладок кон­денсатора соответственно равны

^qm л™ ^qm

А_Фл

I

^qm^ro0

4lc

C

поэтому для этих амплитуд можно записать

^Im =^Аф^4сТъ =■

m

Величина -JL / C называется волновым сопротивлением контура.

Полная электромагнитная энергия контура в любой момент времени будет равна суммарной энергии, запасенной в конденсаторе и катушке индуктивности

где q - заряд на обкладках конденсатора, I - сила тока в контуре.

Электрическое сопротивление R любого реального колебательного контура от­лично от нуля. Поэтому, как мы получили, свободные электромагнитные колебания в реальном колебательном контуре постепенно затухают. Для получения незатухающих электромагнитных колебаний необходимо подводить энергию, компенсирующую поте­ри на джоулево тепло. Если эту энергию будет поставлять источник переменной ЭДС, мы будем иметь дело уже не со свободными, а с вынужденными электромагнитны­ми колебаниями.

Рассмотрим простейший случай вынужденных электромагнитных колебании в контуре, происходящих под действием синусоидальной внешней ЭДС

€ = €_m sin Qt,

где €_m - амплитуда ЭДС, Q - циклическая частота.

Для получения уравнения вынужденных электромагнитных колебаний необходи­мо в закон Ома, записанный для контура, подставить суммарную ЭДС, равную сумме

вынуждающей ЭДС € = €_m sin Qt и ЭДС самоиндукции €_t = :

dt

_r d² q dq q _ ^ L—— + R 1— = €_m sm Qt. dt² dt C ^m

Общее решение этого неоднородного дифференциального уравнения будет пред­ставлять собой сумму общего решения однородного уравнения и частного решения не­однородного. Общее решение однородного уравнения мы уже рассмотрели - это зату­хающие колебания или апериодическое убывание заряда конденсатора. В любом слу-

1

чае, спустя время t >> т = —, этим слагаемым решения можно пренебречь. Тогда ре­шением уравнения останется только частное решение неоднородного уравнения, кото­рое будем искать в виде

I = = I_m sin(Qt + a).

То есть найдем такие значения амплитуды тока I_m и начальной фазы a, чтобы диф-

dq d ² q

ференциальное уравнение обращалось в тождество. Выразим q, —, —— через силу

d

I

t dt²

тока

z' -тЛ

n

Qt + a —

V ² J

Im

Q

q = _ cos(Qt + a) =

sin

Q

dq dt d ² q

f -гг л

•r-4 n

Qt + a +—

V ² J

dt

= I_m sin(Qt + a);

= I_m Q cos(Qt + a) = I_m Q sin

Подставив эти выражения в дифференциальное уравнение, получим

ImLQ sin

n Qt + a +— V 2 J

+ ImR sin(Qt + a) + sin

Qt + a — V 2 J

= €m sin Qt

Л евая часть этого тождества пред­ставляет собой сумму трех гармо­нических колебаний одной частоты, но имеющих разные начальные фазы. Для их сложения удобно воспользоваться методом векторных диаграмм, рассмот­ренным в первой части курса.

И

^€_r

з рисунка видим, что

(1/QC) _QL

tg a =

R

€ €

j _ m ^wm

^m VR ² +[(1/QC) _ QL]^{2 Z} где Z = 4R² +[(1/ QC)- QL]² .

Мы получили, что амплитуда I_m и фаза а вынужденных колебаний зависят от

частоты Q вынуждающей ЭДС.

З

АЧХ заряда

ависимость амплитуды колебаний от частоты называется амплитудно­частотной характеристикой (АЧХ).

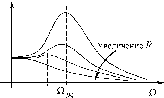
АЧХ тока

Величина Z называется импедансом (impedance, от лат. impedio - препятствую) или полным сопротивлением электрической цепи переменного то­ка. Оно складывается из активного (омического) сопротивления R, реактивного индуктивного сопротивления QL и реактивного емкостного сопротивления

0. / QC. Амплитуда силы тока в контуре зависит не только от параметров контура R, L и C и амплитуды €_т вынуждающей ЭДС, но и от циклической частоты Q .

Независимо от величины R активного сопротивления контура амплитуда силы тока в контуре достигает максимального значения

I

'm

_ = £_т / R

m

при одном и том же значении Q _p циклической частоты вынуждающей ЭДС, равном

ax

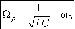
При Q = Q p полное сопротивление контура минимально и равно его активному

сопротивлению. В этом случае а = 0 - сила тока совпадает по фазе с вынуждаю­щей ЭДС.

Явление возрастания амплитуды силы тока в колебательном контуре при при­ближении циклической частоты вынуждающей ЭДС к значению Qp называется яв­лением резонанса тока в электрической цепи, а частота Qp - резонанс­ной циклической частотой тока.

Для амплитуды заряда также будет наблюдаться явление резонанса, но только

0. 2

при слабом затухании (2Р < Ю₀), на резонансной частоте

Колебательный контур с переменной внешней ЭДС представляет собой цепь пе­ременного тока. Для цепей переменного тока законы Ома и Джоуля-Ленца примени­тельно к мгновенным значениям приложенных напряжений и ЭДС, токов и мощностей не справедливы. Чтобы основными законами электрического тока можно было пользо­ваться для цепей переменного тока, кроме приложенного напряжения, нужно учиты­вать возникающую в цепи переменного тока ЭДС самоиндукции.

Действительно, мгновенное значение внешней ЭДС не пропорционально мгно­венному значению силы тока, так как ток отстает от приложенной ЭДС по фазе. Ам­плитудные значения - пропорциональны, а мгновенные - нет.

Закон Ома для переменного тока применим только для амплитуд­ных значений

E = I 7

^wm m ,

где Z - полное сопротивление цепи переменного тока.

Для цепи с последовательно включенными элементами мы получили, что

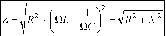
где R — активное сопротивление, а

X = QL — - реактивное сопротивление, которое состоит из

QC

^xL = QL - реактивного индукционного сопротивления,

1

Хс = _{0 п} - реактивного емкостного сопротивления.

QC

Напряжения на емкости и индуктивности находятся в противофазе, следователь­но, X = х^ — Xq .

Напряжения на активном сопротивлении R и на реактивном сопротивлении X сдвинуты по фазе на + — или — —, в зависимости от величин L и C.

Найдем мощность, выделяющуюся в цепи переменного тока.

Выберем начало отсчета времени так, чтобы

1. = I_m cosQt и E = E_m cos(Qt — а),

как на векторной диаграмме, которую мы рассматривали.

Средние значения тока и ЭДС равны нулю (i^ = 0, (Е^ = 0, но среднее зна­чение мощности отлично от нуля P=< Е Ф 0 . Скобками ( ) обозначено среднее значение.

Найдем среднее значение мощности {р = (I_m cosQt • E_m cos(Qt — a)^ . Учиты­вая, что cosP cos у = — [cos(p + y )+ cos(p — y )], получим

^P = ^{— I}m^Em{^{cos(2Qt — a)} + ^cosa) = ^{— I}m^EA^{cos(2Qt — a)}) + ^{— I}m^Em (^cosa) -

Поскольку (cos(2Qt — a)) = 0, а ^cosa^ = cosa, получаем окончательное выражение для закона Джоуля-Ленца для цепей переменного тока

^P ^^Im^€m ^cosa .

Множитель cosa, называемый коэ фф ициентом мощности, отражает сдвиг фаз между внешней ЭДС и током.

Тогда I_mR = €_m cosa и

р=1 Lm r .

В законе Джоуля-Ленца, записанном через амплитудные значения переменного

1

т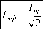 ока, появился коэффициент —, то есть выражение закона получилось разным для по­стоянного и переменного токов. Это весьма неудобно. Чтобы избежать этого неудобст­ва, для характеристики переменного тока и переменного напряжения вместо амплитуд­ных значений используют эффективные (действующие) значения тока и напряже­ния:

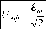
для которых, с одной стороны, закон Ома справедлив так же, как и для амплитудных значений

1. эф^Z = ^Uэф,

а, с другой стороны, закон Джоуля-Ленца может быть записан в таком же виде, как и для постоянного тока. Действительно, закон Джоуля-Ленца для эффективных значений имеет вид

^P = ¹ эф^иэф ^cosa .

С учетом закона Ома имеем = I^Z cosa. Поскольку R = Z cos a, то для эффек­тивного значения силы тока можем записать закон Джоуля-Ленца в окончательном виде

Если цепь содержит только реактивное сопротивление (R = 0), то cosa = 0 и средняя мощность будет равна нулю при любых токах и напряжениях. Если коэффици­ент мощности cos a мал, то для передачи мощности при заданном напряжении необ­ходимо увеличивать силу тока, что либо приведет к увеличению джоулевых потерь, либо, чтобы этого не происходило, потребует увеличения сечения проводов, что повы­шает стоимость линий электропередач. Поэтому на практике в качестве наименьшего допустимого значения принимают cos a = 0,85.

Физика волновых процессов

И в первой части курса физики, и в предыдущем разделе мы рассматривали про­цессы, периодически повторяющиеся во времени. Это механические колебания, в пер­вой части, и электромагнитные колебания, только что нами рассмотренные.

Если колебательный процесс происходит в пространстве, части которого «связа­ны» друг с другом, то в периодический процесс вовлекается все большая область про­странства. В этом случае говорят о распространении колебаний или о волновом про­цессе. Волновые процессы встречаются во многих областях физики. Это и волны на воде, и звуковые волны, и свет. Как мы увидим позже в этой же части курса, электроны и другие частицы в некотором отношении тоже подобны волне.

К изучению волновых процессов мы и переходим в данном разделе. Сначала мы рассмотрим общие определения волновой физики, применимые для всех волн, при этом основное внимание мы будем уделять электромагнитным волнам, частным случа­ем которых является свет. Далее на примере световых волн рассмотрим два основных явления волновой физики - интерференцию и дифракцию волн. И закончим раздел изучением основных явлений, возникающих при взаимодействии света с веществом.

Тема: Волновая физика

Вопросы:

1. Волновые процессы. Определение.

2. Классификация волновых процессов.

3. Трехмерное и одномерное волновое уравнение в однородной изотропной среде.

4. Характеристики волновых процессов

5. Электромагнитные волны. Свойства. Уравнение и график монохроматической плоской бегущей волны.

6. Понятие о световых волнах. Характеристики. Оптический показатель преломления.

Мы знаем, что колебательный процесс - это процесс, при котором изменение параметров, описывающих состояние системы, периодически повторяется со време­нем. Колебательный процесс, или колебание, происходит в ограниченной области про­странства. Он характеризуется периодом T или частотой колебаний V .

В отличие от колебаний волновой процесс является периодически повто­ряющимся процессом, который распространяется в пространстве с некоторой ко­нечной скоростью. Другими словами, волновой процесс или волна - это процесс распространения колебаний. При этом вещество (или поле) не переносится волной, а только вовлекается в колебательный процесс, происходящий относительно равновес­ных состояний. В волновом процессе переносится энергия и импульс.

Волновой процесс характеризуется частотой (распространяющихся) ко­лебаний V (циклической частотой Ю = 2^V) и скоростью распростра­нения (колебаний) V.

Волновым фронтом называется поверхность, которая разделяет про­странство на две области: в одной из них колебания уже происходят, до второй об­ласти колебания еще не дошли.

Волновой поверхностью называют поверхность, в точках которой ко­лебания имеют одинаковую фазу.

Форма волновой поверхности в однородных изотропных средах совпадает с фор­мой волнового фронта.

Рассмотрим классификацию волн, исходя из определения волны.

• По характеру периодического процесса волны бывают скалярные, когда невозможно указать пространственное направление колебаний (волна температуры) и векторные, когда колебания происходят в определенном направлении (колебание частиц воздуха в звуковой волне). При этом сам колеблющийся параметр также может быть скалярным (давление в звуковой волне) или векторным (напряженность элек­трического поля в электромагнитной волне).

• По частотным характеристикам волны делятся на две группы: монохроматические волны - распространяется гармоническое колебание с частотой Ю;

немонохроматические волны - одновременно распространяют­ся различные колебания с разными частотами.

По природе волны делятся на:

• механические - распространение упругих (механических) колебаний вещества (например, звук).

• электромагнитные - распространение колебаний электромагнит­ного поля (например, свет).

В зависимости от направления колебаний волны делятся на два типа:

• продольные волны - колебания происходят вдоль направления распространения волны (например, звук);

направление распространения волны

направление колебаний

• поперечные волны - колебания происходят перпендикулярно рас­пространению волны, такая волна называется (например, электромагнит­ные волны).

А

направление распространения волны

у направление колебаний

• Среди волн по форме волнового фронта выделяют:

• сферические волны - волновой фронт является сферой. Например, излучение точечного источника в однородной изотропной среде.

- плоские волны - волновой фронт является плоскостью.

Волновой фронт

Направление распространения волны

Волновые процессы описываются волновым уравнением, решением которого они являются.

Вспомним колебания. Уравнение свободных гармонических колебаний имеет вид

d² x 2 Л Ь ЮдX = 0 .

dt

Его решением является функция, описывающая гармонический колебательный процесс x(t) = x₀ cos(®₀t + ф).

Волновое уравнение имеет несколько похожий вид, оно представляет со­бой дифференциальное уравнение второго порядка в частных производных

или

Здесь греческой буквой ^ («кси») обозначен колеблющийся параметр, А - дифферен­циальный оператор Лапласа (P. Laplace, 1749-1827), для которого используется гре­ческая буква «дельта» А (не путать с приращением). Поскольку ^(г, t) является

функцией нескольких переменных, уравнение записывается не в полных производных, как для колебаний, а в частных производных.

Используемый дифференциальный оператор Лапласа можно представить через

2

другой дифференциальный оператор А = V . Дифференциальный оператор V («на- бла») определяется в декартовой системе координат как формальный вектор с проек-

( д д д Л ^-д ^-д ^-д

циями ——, ——, — или V = I Ь j Ь k —, тогда его действие на скалярную

^дх ду дг) dx ду д2

функцию ф можно записать

дх ² ду ² д2²

где i , j, k - орты декартовой системы координат. Оператор V ставит в соответствие произвольной скалярной функции ф векторную функцию с проекциями на оси декар-

дф дф дф товой системы координат ——, ——, ——.

дх ду д2

В развернутом виде в декартовой системе координат, учитывая, что д²^ д²^ д²^

^ дф^- дф^- дф^- 2 ^Vф =dX' + ^^J + &^k■ ^{тогда Аф} = ^{V ф}

, трехмерное волновое уравнение записывается следующим

образом:

д ²ф д ²ф д ²ф + —f +

2

2

+ ■

дх ду д2

д²^ д²^ д1 а

—- ч ч = -

дх ² ду ² dz ² V ² dt²

Любая функция вида

^, t) = Wt + r)

является решением волнового уравнения, здесь Ъ(т, t) = х, у, z, t), где r - радиус- вектор, которому можно сопоставить три декартовые координаты (х, у, z) . Таким об­разом, любая периодическая функция, зависящая от времени t и координат r , яв­ляется волной, если r и t связаны по закону r + Vt.

Если волна распространяется вдоль одного направления, тогда уравнение стано­вится одномерным волновым уравнением. Одномерное волновое уравнение при рас­пространении волны вдоль оси Ox имеет вид

d!i_ 1_ d!i dx² = v ² at².

Являющиеся его решением функции вида £,(Vt + х) описывают плоские волны: £,(Vt - х) - плоская бегущая волна, распространяющаяся в положительном направ­лении оси х ;

£,(Vt + х) - плоская бегущая волна, распространяющаяся в отрицательном направ­лении оси х .

Здесь t - время, х - координата, V - скорость распространения волны.

Характеристики волн естественно связаны с характеристиками колебаний волны. Безразмерный аргумент функции Ъ(г + Vt), описывающей волновой процесс,

н

t + —

V V ^V уу

Ю

азывается фазой волны. Фаза плоской волны <Z,(Vt + х) =

V

. Здесь Ю - частота колебаний, называемая для волнового процесса

имеет

вид Ю

частотой волны.

Скорость распространения колебаний, которую мы назвали скоростью волны, является ф а з о в о й с к о р о с т ь ю в о л н ы . Она определяет скорость, с которой перемещается поверхность постоянной (одинаковой) фазы волны.

Минимальное расстояние между двумя точками, в которых фаза колебаний оди­накова в один и тот же момент времени, называется длиной волны X . Волна (плоскость постоянной фазы волны) проходит за один период колебаний T путь, рав­ный длине волны X . То есть,

X = VT.

Волна называется г а р м о н и ч е с к о й , если распространяющиеся колебания яв­ляются гармоническими.

График монохроматической плоской волны

Д

График плоской волны

ля гармонических волн вводят понятие амплитуды волны, которая равна амплитуде гармонических колебаний в данной точке пространства.

Ин тенсивностью волны называется количество энергии, переносимой волной в единицу времени через единичную площадку, перпендикулярную распростране­нию волны. Для гармонических волн интенсивность пропорциональна квадрату ампли­туды волны.

Волновым числом называют величину, равную отношению частоты ко-

1. ю 2п 2п

лебаний к фазовой скорости волны k = - = —-- = ^—. Тогда плоскую волну, являю-

• IV А

щуюся решением одномерного волнового уравнения, можно представить в виде <^(ю? + kx).

Если волновое уравнение трехмерное, то его решением может быть плоская вол­на, которую можно записать в виде <^(ю? + kr), где k - волновой вектор, на­правление которого совпадает с направлением распространения волны, а величина

, 2 п ^

k = —г~; r - радиус-вектор точки, в которой рассматриваем

р

А

авна волновому числу волну.

Основные понятия физики волн мы определили, и далее мы будем рассматривать волновые процессы на примере электромагнитных волн, частным случаем которых являются световые волны или свет.

Э

процесс распространения в пространстве

лектромагнитная волна

возмущения электромагнитного поля.

Существование электромагнитных волн является следствием уравнений Максвел­ла. Для электромагнитного поля вдали от порождающих его свободных зарядов и мак­ротоков эти уравнения имеют вид

IDdS = 0;

(S)

I BdS = 0.

(S)

(S)

(L)

д—

дг

—» —»

(S)

(L)

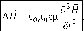
Если среда однородна и изотропна, то D = ss oE и B = ^q H. В этом случае

J HdS = 0.

( s )

Если из этих уравнений вывести уравнения для векторов напряженностей E и H, то получим волновые уравнения

уравнения Максвелла можно переписать

| Edl =-^q J -—dS;

и

Это значит, что напряженности E и H переменного электромагнитного поля в однородной, изотропной, непроводящей, нейтральной среде должны удовлетворять волновому уравнению, то есть переменное электромагнитное поле будет распростра­няться в пространстве в виде волны.

Сравнивая полученные уравнения с волновым уравнением, записанным в общем

виде, At = —- t, находим фазовую скорость электромагнитных волн

V² dt²

J EdS = 0;

( s )

(S)

JHdl = ss_q J ~^DdS;

(L) (S)

(L)

или	V с л/ф	, где

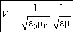
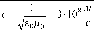
В вакууме S = ^ = 1 и, соответственно, V = С. Таким образом, величина

м

с = 3•1Q⁸ — есть скорость распространения электромагнитных волн в вакууме.

с

Из уравнений Максвелла следует также, что в однородной и изотропной среде

—*■ —*■ к, E	= кЛ	ЦЦо £		—► —► к, H	= - кл КE
	V	о s s			V№o

где квадратные скобки обозначают, как обычно, векторное произведение векторов. Откуда видно, что электромагнитные волны в однородной изотропной среде пред­ставляют собой поперечные волны (E ^ к иH ^ к ), кроме того, вектор напря­женности электрического поля E перпендикулярен вектору напряженности маг­нитного поля Н, и оба поля колеблются в фазе.

Векторы E и Н вместе с волновым вектором к образуют правую тройку векто­ров (E, H, к). То есть при вращении правого буравчика от первого вектора ко второму в сторону меньшего угла его поступательное движение будет направлено по третьему

вектору. Циклические перестановки векторов H, к, E или к, E, H также будут обра­зовывать правую тройку.

Если ось Ox выбрана по направлению распространения волны, то ось Oy можно выбрать так, что вектор напряженности электрического поля плоской монохроматиче­ской электромагнитной волны будет направлен по оси Oy E_y = Eq C0s(rat — kx + ф),

тогда E_x = E_z = 0. Вектор напряженности магнитного поля этой волны будет иметь составляющие H_z = Hq C0s((Dt — kx +ф) и H_x = H_y = 0. На рисунке представлен

п

случай ф = — и x = 0 при t = 0, тогда E_y = Eq sin( rat — kx) и H_z = Hq sin(rat — kx). 2 ^y

Э

S

лектромагнитные волны, как любые волны, не переносят вещество - это распро­страняющиеся электрические и магнитные поля, они переносят электромагнитную энергию. Для характеристики переноса энергии используют векторное произведение напряженностей электрического и магнитного поля - вектор Пойнтинга (J. Poynting, 1852-1941), введенный Джоном Пойнтингом в 1884 году

E, H

Вектор S является вектором плотности потока электромагнитной энергии. Он по­казывает, в каком направлении и какое количество энергии переносится за единицу времени через единичную площадку, расположенную перпендикулярно распростране­нию волн.

П

РРо /_Я2

SS_n \

I=(	S	к	SS 0
\		' V	РРо \

'.E²) =

Электромагнитные волны кроме энергии переносят импульс, и поскольку волны поглощаются и отражаются, они передают импульс поглощающей или отражающей поверхности, то есть оказывают на нее давление. Полученное Дж. Максвеллом в 1873 году выражение для давления плоской монохроматической электромагнитной волны при нормальном падении на поверхность с коэффициентом отражения R

1. ? P = ^ ssq E ²(1 + R)

о определению интенсивности волны она равна среднему значению модуля вектора Пойнтинга, при этом усреднение должно проводиться или за целое число пе­риодов или за время, много большее периода колебаний,

было экспериментально доказано в 1900 году П. Н. Лебедевым (1866-1912). Из-за ма­лости величины давления, например, давление света Солнца на поверхность Земли со­ставляет P * 5 мкПа, измерение давления потребовало изобретательности и мастер­ства.

При падении плоской волны на поверхность под углом а давление, оказываемое волной на поверхность, описывается выражением

P = 1 ss ₀ E ²(1 + R)cos² а.

То, что свет ведет себя подобно волне, было установлено за много лет до Мак­свелла. Но никто не мог сказать, что это за волна, то есть распространением каких именно колебаний является свет. Максвелл, основываясь на своей теории, утверждал, что свет - это электромагнитная волна.

Эта точка зрения постепенно получила признание, хотя большинство ученых по­началу считали волны, получающиеся из уравнений Максвелла, абстрактными волна­ми, не имеющими физического смысла. Окончательно точка зрения Максвелла получи­ла признание лишь после того, как в 1887 году Генриху Герцу (H. Hertz, 1857-1894) впервые удалось генерировать и наблюдать электромагнитные волны на опыте.

В качестве источника электромагнитных волн был использован колебательный контур. Герц, уменьшая число витков катушки индуктивности, а также разворачивая пластины конденсатора, чтобы они лежали в одной плоскости, перешел от закрытого колебательного контура, переменное электрическое поле в котором сосредоточено ме­жду пластинами конденсатора, а магнитное - внутри катушки индуктивности, к от­крытому колебательному контуру - вибратору Герца, переменное поле кото­рого заполняет окружающее его пространство.

Имея широкий диапазон частот V = —— (или длин волн X = VT = —), электро-

2п V