Будем считать, что электрон в атоме движется со

скоростью V по круговой орбите радиусом r.

Направления движения электрона и тока I указаны на рисунке стрелками.

Согласно определению магнитного момента тока величина орбитального магнитного момента i -го элек­трона равна

где S - площадь орбиты электрона. Вектор p_mi направлен в ту же сторону, что и маг-

гг 2пг

нитное поле в центре кругового тока I . Обозначим через T = период обращения

К

электрона. Тогда

е eV		eVr
T 2пг	и	pmi = 2

В атомах диамагнетиков четное число электронов, и в среднем половина элек­тронов имеет магнитные моменты, направленные в одну сторону, половина - в проти­воположную сторону. Суммарный магнитный момент атома равен нулю.

Во внешнем магнитном поле электроны, имеющие магнитные моменты, проекция которых на направление поля отрицательна, получат дополнительное вращение. Наоборот, электроны, проекция магнитных моментов которых на направление поля по­ложительна, замедлят свое вращение. Магнитный момент первых увеличится, а вторых

• уменьшится. И суммарный момент атома станет неравным нулю по величине и на­правленным в среднем против внешнего поля. При этом атом будет создавать собст­венное магнитное поле, направленное против внешнего.

В атомах парамагнетиков число электронов нечетное и суммарный магнитный момент атома в отсутствии внешнего поля отличен от нуля. Направлены магнитные моменты атомов хаотически, в результате чего суммарный момент всех атомов будет равен нулю. Намагничивание парамагнетиков связано с поворотом магнитных момен­тов атомов (контуров с микротоками) магнитным полем по направлению поля. Упоря­дочивающему действию магнитного поля препятствует разупорядочивающее действие теплового движения. Зависимость магнитных свойств парамагнетиков от температуры описывается законом Кюри

1

Х~

Т

Ферромагнетизм имеет квантовую природу и не может быть объяснен с пози­ции классической физики. Ферромагнетики состоят из областей спонтанной намагни­ченности - доменов, размером 10 ³ —10 ² см. Каждый домен имеет ненулевую

намагниченность. Суммарная намагниченность ферромагнетика может быть любой -

от нулевой намагниченности до максимальной намагни- домены ченности, которая достигается, когда магнитные моменты

в сех доменов сонаправлены. Согласованная намагничен­ность атомов в домене связана с перекрытием квантовоме­ханических волновых функций электронов, входящих в атомы, которое приводит к ориентации спинов электронов параллельно друг другу. О квантовомеханическом описа­нии электронов и атомов мы будем говорить дальше, в раз­деле квантовая физика.

Рассмотрим, как происходит намагничивание ферромагнетиков.

I этап (слабые магнитные поля) - намагничивание (увеличение намагниченности), связанно с движением границ доменов. Домены, магнитный момент

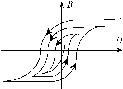
которых направлен по полю, имеют минимальную энергию (находятся в состоянии устойчивого равновесия). Домены, имеющие направление магнитного момента, близкое к направлению действующего внешнего поля, увеличиваются по размеру. Домены, имеющие магнитные моменты, направленные навстречу полю, имеют максимальную энергию (их состояние неустойчиво), они уменьшаются в размерах. На первом этапе процесс намагничивания обратим.

2. этап - необратимое смещение границ доменов. Вследствие наличия дефектов сильное смещение границ происходит скачкообразно с потерями энергии. Маленькие домены поглощаются увеличивающимися доменами. В конце этапа остается один до­мен с наиболее «благоприятной» ориентацией магнитного момента.

3. этап - магнитный момент оставшегося домена ориентируется по полю, то есть происходит доворачивание магнитных моментов. Это парапроцесс - увеличение намагниченности в результате упорядочивания магнитных моментов отдельных ато­мов.

I II III

Процесс намагничивания на втором этапе яв-

ляется необратимым, и при уменьшении внешнего ^{I II III} поля кривая намагниченности В(Н ) будет иметь другой вид.

Явление, связанное с различным значением намагниченности в одном и том же магнитном поле (в зависимости от предыстории), называется явлением гистерезиса (от греч. hysteresis - отставание, запаздывание), а график - петлей гистерезиса. Hс - коэрцитивная сила (от

лат. coercitio - удерживание), значение напряженности магнитного поля, необходимого для достижения нулевой намагниченности или нулевой магнитной индукции в ферро- магнитном веществе. Различают коэрцитивную силу мНс, когда становится равной нулю намагниченность J, и коэрцитивную силу

вНс, когда в веществе становится равной нулю магнитная индукция.

Технология размагничивания ферромагнети- ков заключается в перемагничивании с уменьше- нием петли гистерезиса. Изменяя направление на- магничивающего поля, постепенно уменьшают его величину.

Жесткие ферромагнетики имеют большую по площади петлю гистерезиса, их трудно

	\
	ж

Вг

/	\
\	/

Вг

В,

Во = 0

перемагничивать, из них делают постоянные магниты. У мягких ферромагнетиков петля гистерезиса меньше, они легче перемагничиваются, и их используют в электро­магнитах.

Ферромагнетики обладают явлением магнитострикции - изменением раз­меров и формы тела при намагничивании. Это вызывается изменением энергетического состояния кристаллической решетки в магнитном поле и, как следствие, расстояний между узлами решетки.

При высоких температурах ферромагнетики становятся парамагнетиками (фазо­вый переход второго рода/ Температура, при которой теряются ферромагнитные свойства, называют точкой Кюри. Все ферромагнетики имеют свою точку (темпера­туру) Кюри. Для железа точка Кюри соответствует 770 °С, для никеля 360 °С, а для пермалоя (сплав 70 % Fe и 30 % Ni) всего 70 °С.

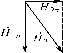
На границе раздела двух магнетиков магнитное поле претерпевает скачкообраз­ное изменение. Граничные условия, определяющие магнитное поле на границе разде­ла двух магнетиков, можно получить из теоремы о циркуляции напряженности магнит­ного поля в отсутствии токов и теоремы Гаусса для индукции магнитного поля -

| Hdl = 0 и | BdS = 0.

(

(L)

S)

#1т= H _2т;

B

Ж.

2 2 ^;

1т

B

2т

^B1n ^B2n;

H

Ж

21

1n

H

2n

	BiT	B2 X Ц1
к tcq" t-H	ч ^
Ц 2		VIЦ 2
	B2 n	\l
	У	, ^B2

где H_T, B_T, и H_n, B_n - соответственно тангенциальные и нормальные составляю­

щие векторов H и B, 21 и 22 - магнитные проницаемости (на рисунке 21 > 22 ).

Тема: Уравнения Максвелла

Вопросы:

1. Ток смещения.

2. Полная система уравнений Максвелла в интегральной форме.

Мы уже рассмотрели в предыдущих темах почти все законы, входящие в систему уравнений Максвелла (J. Maxwell, 1831-1879). Перечислим их.

Начнем с закона электромагнитной индукции Фарадея, определяющего ЭДС индукции, возбуждаемую в неподвижном замкнутом проводящем контуре,

Изменяющееся магнитное поле создает в любой точке пространства вихре­вое электрическое поле независимо от того, находится в этой точке проводник или нет. Сформулированное таким образом последнее равенство является одним из урав­нений Максвелла : циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру L равна взятой с обратным знаком скоро­сти изменения магнитного потока сквозь поверхность, натянутую на контур.

По определению магнитный поток Ф_т = J BdS . Считая поверхность интегриро-

(S)

вания S, образованную неподвижным контуром L, неподвижной, получим

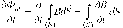
Поэтому рассматриваемое уравнение Максвелла можно записать в виде

JEdl = - J —dS ^{J J} dt

где направление обхода контура L и вектор dS согласованы между собой по правилу правого буравчика.

Следующий закон - закон полного тока, определяющий циркуляцию магнитного

поля

JBdl = ц₀(I +1'), JHdl = I,

(L) (L)

где I и I' - сила результирующего макротока и микротока, соответственно, сквозь поверхность, образованную замкнутым контуром L .

Максвелл обобщил закон полного тока. Согласно гипотезе Максвелла, кроме то­ков (макротоков в проводниках и микротоков в магнетиках), существует еще одна при­чина возникновения магнитного поля. Точно так же, как изменение магнитного поля приводит к появлению электрического, изменение электрического поля должно приво­дить к возникновению магнитного.

Максвелл проделал мысленный эксперимент. Он рассмотрел заряжающийся кон­денсатор.

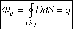
B

B

B

I

®

B

©

B

®

B

В области подводящих проводов при протекании тока заряда конденсатора возни­кает магнитное поле. Поле не может оборваться в области, где расположен конденса­тор, хотя там нет проводов, и между пластинами конденсатора ток не протекает. Что же

является источником магнитного поля внутри кон­денсатора? Изменяющееся при заряде конденсатора электрическое поле между обкладками конденсато­ра создает магнитное поле подобно некоторому гипотетическому току, названному Максвеллом током смещения.

Этот ток смещения Максвелл использовал в качестве количественной характеристики «магнит­ного действия» изменяющегося электрического по­ля. Посмотрим, как он его определил. По теореме Г аусса, которую мы получили в пер­вой части нашего курса, поток вектора D (электрического смещения) сквозь замкну­тую поверхность S

где q - алгебраическая сумма свободных электрических зарядов, охватываемых замк­нутой поверхностью S . Продифференцируем это выражение по времени

d0_e _ d dt dt

dq

dt

f DdS.

(S)

Если поверхность S неподвижна и не деформируется, то изменение во времени

потока вектора электрического смещения D сквозь поверхность S вызывается только изменением электрического смещения с течением времени. Поэтому полную производ­ную, стоящую в правой части уравнения, можно заменить частной производной по времени и дифференцирование внести под знак интеграла:

dq dt

Левая часть этого выражения имеет размерность силы тока = I = f J dS, то-

d

S

t

dD

и

гда производная

dt

меет размерность плотности тока. Поэтому Максвелл предло-

п

dD

dt

жил назвать величину

лотностью тока смещения:

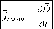
Плотность тока смещения в данной точке пространства равна ско­рости изменения вектора электрического смещения в этой точке.

Током смещения сквозь произвольную поверхность S называется некото­рый гипотетический (несуществующий) ток, сила которого численно равна потоку вектора плотности тока смещения сквозь эту поверхность:

Тогда в случае нестационарных полей закон полного тока примет вид

f

dD

dt

dS.

^Я <я = f|7

(L)

Добавив теорему Гаусса для электрического и магнитного полей, получим полную систему уравнений Максвелла, которая в интегральной форме записи имеет вид:

f Edl = — f dS - Закон электромагнитной индукции Фарадея.

^{J J} dt

(

(L)

S)

dD

dt

f DdS = f pdV

(S) (V)

fм =\[i+

(L) (S)V

BdS = 0

( s )

• Теорема Гаусса для электрического поля.

dS - Закон полного тока.