Мы получили линейное дифференциальное уравнение. Проинтегрируем его, за-

I U t

d

писав в виде

I dt r dI r dt

• — —, то есть найдем — — — .

& — IR L ^J₀ & — IR ^J₀ L

1 ( & — IR^л — ln R

t

— или

L

Откуда

&

v

	( t \
, &
I = —	1 — e X
R
	V у

L

где T — — называется постоянной времени. Значение X соответствует времени, за

R

С

1—1

v e

I max — 0,63I _max или 63 % своего

которое сила тока достигает значения I

максимального значения.

Если отключить источник ЭДС, то в результате возникновения ЭДС самоиндук­ции, препятствующей убыванию силы тока, сила тока уменьшится до нуля не мгновен­но. В этом случае дифференциальное уравнение, описывающее происходящий процесс,

будет иметь вид L Ъ RI — 0 , так как & — 0. После интегрирования получим

dt

L

где T — — - та же постоянная времени, а i о - начальная сила тока. За время X сила R

тока убывает в e — 2,71...раз.

Тема: Магнитные свойства вещества

Вопросы:

1. Магнитные свойства вещества. Намагниченность.

2. Закон полного тока в магнитных средах.

3. Магнитное поле в веществе. Напряженность магнитного поля.

4. Классификация магнетиков. Свойства. Характеристики.

5. Диамагнетики. Классическое описание.

6. Парамагнетики. Закон Кюри.

7. Ферромагнетики. Природа ферромагнетизма.

8. Намагничивание ферромагнетиков. Гистерезис. Точка Кюри.

9. Магнитное поле на границе магнетиков.

В прошлой теме мы рассматривали токи, текущие по проводникам, и токи, обу­словленные движением зарядов в свободном пространстве, - их называют макро­токами.

Кроме макротоков в веществе существуют микротоки, обусловленные движе­нием электронов в атомах и молекулах. Эти микротоки создают внутреннее магнитное поле - собственное поле магнетика.

Результирующее магнитное поле B в веществе складывается из внешнего Bq и собственного B' магнитных полей

B = В₀ + B'.

Для количественного описания магнитных свойств вводят понятие намагни­ченности J - магнитный момент единицы объема вещества

1

I р.

ду

J = lim

ду AV

г

суммарный магнит-

де p_m - магнитный момент i -го атома или молекулы, I Pmi

AV

н

В однородных материалах

где P_m

ый момент в объеме AV.

суммарный магнитный

момент всех атомов или молекул в объеме материала V .

Найдем индукцию собственного магнитного поля магнетика.

Д ля простоты рассмотрим область вещества, представляющую собой цилиндр длиной l, площадью поперечного сечения S. Допустим, что все микротоки текут в плоскостях, параллельных основанию цилиндра. Тогда все микротоки в объеме вещества компенсируют друг друга, так как они протекают навстречу друг другу. Реально действие всех микротоков сводится к тому, что по поверхности потечет ток I'. Следовательно,

микротоками, будет полем, созданным протекающим по поверхности током I', и его индукция будет равна индукции магнитного поля соленоида

N I'

ТЭ? Tf

^B - ^ц о ~y ^{- ц0} у ■

Мы рассматриваем как бы один виток ( N — 1), «размазанный» по длине l ■

I' V

Магнитный момент этого тока I будет равенp_m — IS — —-—, где V- объем вещества.

Г

Тогда намагниченность J — — —. Подставляя I — Jl в выражение для

• l

индукции B', получим B — цо J . Тогда суммарное поле будет равно

в — B₀ + в ' — B₀ + ц ₀J.

Посмотрим, как изменятся законы, описывающие магнитное поле при наличии вещества. Запишем с учетом микротоков закон полного тока для магнитного поля в

веществе (теорему о циркуляции вектора B): циркуляция вектора B по произ­вольному замкнутому контуру будет равна алгебраической сумме токов проводимо­сти и молекулярных токов, охватываемых этим контуром, умноженной на магнит­ную постоянную

I Bdl — | B_ldl — ц ₀(I +1' ),

(L) (L)

где dl - элемент длины контура, направленный вдоль обхода контура; Bl - состав­ляющая вектора B в направлении касательной контура L произвольной формы; I - суммарная сила тока свободных зарядов (макротоков или токов проводимости) и I - суммарная сила молекулярных токов (микротоков), охватываемых контуром L ■

С учетом, что B — Bo + B' — Bq + Ц о*, закон полного тока примет вид

f(^Bo + ^ц о *7) ^d~l ^{— ц} о (^I + ^ )■

(L)

В отсутствии вещества ( J — 0 и I' — 0 ) получим | Bq dl — цqI, тогда

(L)

• циркуляция намагниченности равна суммарному току намагничивания (сумме микротоков).

Выразив Bq — B — B' — B — цо J и учитывая, что | Bqdl — цqI, можем за-

(L)

писать

dl = I.

B

f

(L)

— ^ о J

Мы получили, что циркуляция некоторого выражения по замкнутому конту-

2. 0

ру равна суммарному макротоку. Этому выражению приписан физический смысл на­пряженности магнитного поля

Тогда закон полного тока для напряженности будет иметь вид

f Hdl = I.

(L)

Здесь I - сила суммарного макротока, охватываемого контуром L. Циркуляция на­пряженности магнитного поля равна суммарной силе тока, текущего по проводни­кам (реального тока), охваченного контуром, независимо от присутствия магнитных

веществ. Вектор H обычно ассоциируется со свободными токами (макротоками), век­тор намагниченности J - с токами намагничивания (микротоками), а вектор B - со всеми токами.

Суммарное поле теперь мы можем записать в виде выражения

B = Bq + B = 2 о H + 2 о J = 2 о (H + J),

связывающего между собой векторы индукции магнитного поля B, напряженности H

и намагниченности J.

В не очень сильных магнитных полях и однородных и изотропных средах можно считать, что намагниченность пропорциональна напряженности магнитного поля J ~ H или

,

коэффициент пропорциональности % называют магнитной восприимчивостью ве­щества.

Магнитная восприимчивость вещества - безмерная величина, ха­рактеризующая свойство вещества намагничиваться в магнитном поле и равная от­ношению намагниченности вещества к напряженности магнитного поля.

Кроме восприимчивости, для описания магнитных свойств веществ используют магнитную проницаемость

2. = 1 + X.

Тогда в однородных и изотропных средах

^B = 2 о⁽¹ + X^)H = 2 o2^H.

Поскольку микротоки существуют во всех веществах, то все вещества являются магнетиками, то есть обладают магнитными свойствами.

Вещества, обладающие диамагнитными свойствами

П

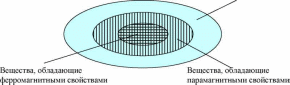
Классификацию веществ по магнитным свойствам можно изобразить так.

оясним рисунок.

Все вещества обладают диамагнитными свойствами. Диамагнетиками яв­ляются только те из них, которые другими свойствами не обладают. Оставшиеся веще­ства обладают парамагнитными свойствами, значительно более сильными, чем диа­магнитные свойства, в связи с чем, в парамагнетиках диамагнитными свойствами можно пренебречь. Часть парамагнетиков обладает более сильными ферромагнитны­ми свойствами.

Диамагнетики - вещества, в которых во внешнем магнитном поле возни­кает собственное магнитное поле, направленное противоположно внешнему намагни­чивающему полю. В отсутствии внешнего поля собственное поле диамагнетика равно нулю.

Свойства диамагнетиков:

• B' U B₀;

• выталкиваются из внешнего магнитного поля;

• магнитная проницаемость ц * 1;

• магнитная восприимчивость отрицательна X < 0 и IX * 10^—6 —10^—5.

К диамагнетикам относятся почти все газы (кроме кислорода), золото, серебро, медь, органические вещества.

Диамагнитные свойства обусловлены наведением в веществе внешним магнит­ным полем магнитных моментов атомов, магнитный момент которых в отсутствии поля равен нулю.

Парамагнетики - вещества, в которых вектор магнитной индукции собст­венного магнитного поля сонаправлен с вектором магнитной индукции намагничиваю­щего поля. В отсутствии внешнего магнитного поля собственное поле парамагнетика равно нулю.

Свойства парамагнетиков:

• B ТТ в₀;

• втягиваются во внешнее магнитное поле;

• магнитная проницаемость ц * 1;

_—5 _—3

• магнитная восприимчивость положительна X > 0 и X * 10 — 10 .

Парамагнетиками являются кислород, платина, алюминий, все редкоземельные металлы.

Атомы диэлектрических парамагнетиков имеют ненулевой магнитный момент в отсутствии магнитного поля, но намагниченность в отсутствии поля равна нулю, что связано с разупорядоченностью магнитных моментов атомов. При наличии внешнего магнитного поля происходит упорядочивание магнитных моментов атомов по внешне­му полю. У металлов значительный вклад в намагниченность дают свободные электро­ны (не связанные с атомами).

Ферромагнетики - вещества, обладающие спонтанной намагниченностью (намагничены) даже при отсутствии внешнего магнитного поля.

Свойства ферромагнетиков:

• B'TT B₀;

3 5

• магнитная проницаемость 2 = 10 ... 10 ;

3. 5

• магнитная восприимчивость положительна % > 0 и % ~ 10 — 10 .

К ферромагнетикам относятся металлы группы железа - железо, кобальт, ни­кель и др.

З ависимость индукции магнитного поля B и намагниченности J от напряженно­сти H для разных типов магнетиков имеет вид (не в масштабе):

Рассмотрим качественно классическую теорию диамагнетизма и парамагне­тизма. По классическим представлениям электроны в атоме вращаются вокруг ядра. Магнитный момент p_mi электрического тока, вызванного движением i -го электрона по орбите, называется орбитальным магнитным моментом электрона. Вектором орбитального м а г н и т н о г о м о м е н т а а т о м а P_m называется векторная сумма орбитальных магнитных моментов всех его электронов (магнитный момент ядра при­мерно в 2000 раз меньше, и им пренебрегают)

z

^p m = ^P mi .

i =1 ^