Тема: Дифракция волн

Вопросы:

1. Понятие о дифракции волн. Принцип Гюйгенса-Френеля.

2. Зоны Френеля. Метод зон Френеля.

3. Дифракция Френеля на круглом отверстии.

4. Дифракция Фраунгофера на щели.

5. Дифракционная решетка.

6. Области дифракции и прямолинейного распространения.

Дифракцией называют совокупность явлений, наблюдающихся при распро­странении света (волн) в среде с резко выраженной неоднородностью, например, при наличии препятствий. Дифракция наблюдается при размерах неоднородности среды порядка длины волны.

Часто дифракцию определяют как явление огибания волнами препятствий. Дей­ствительно, это одно из характерных явлений, наблюдающееся при дифракции.

Между интерференцией и дифракцией нет принципиального физического разли­чия, оба явления заключаются в перераспределении светового потока при суперпози­ции (наложении) когерентных волн. Когда речь идет о суперпозиции конечного числа волн, говорят об интерференции, если - бесконечного числа волн, то говорят о ди­фракции.

Для количественного описания явления дифракции не требуется никаких новых принципов. Дифракционная задача для электромагнитных волн сводится к решению уравнений Максвелла. Однако в такой строгой постановке дифракционные задачи, в виду их сложности, допускают аналитическое решение лишь в очень простых случаях. Нас будет интересовать дифракция только световых волн. И рассматривать мы будем только те методы решения дифракционных задач, которые основаны на нестрогих принципах. Несмотря на свою нестрогость данные методы имеют в оптике большее значение.

Для качественного описания огибания волной препятствий, нахождения формы и положения фронта волны, используют принцип Гюйгенса (H. Huygens, 1629-1695).

Принцип Гюйгенса : все точки волнового фронта можно рассматривать как источники вторичных сферических волн, распространяющихся только вперед. Положение волнового фронта исходной (первичной) волны, есть огибающая волновых фронтов всех вторичных волн.

К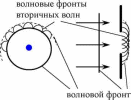 аждая точка волнового фронта точечного источника представляет собой вторич­ный сферический источник, и спустя некоторое время огибающая фронтов вторичных волн представляет собой сферу. Для плоской волны волновой фронт представляет со­бой плоскую поверхность. Если на пути плоской волны есть препятствие, то огибаю­щая фронтов вторичных волн не будет плоской, в этом случае волновой фронт изменит свою форму.

Интенсивность световых волн за препятст­вием на основании принципа Гюйгенса рассчи­тать нельзя, поскольку принцип Гюйгенса являет­ся чисто геометрическим.

Для нахождения интенсивности света прин­цип Гюйгенса был уточнен Френелем (O. Fresnel,

1788-1827) И получил название принципа Гюйгенса-Френеля. Он состоит из не­скольких основных положений: первичной волны

1. При расчете амплитуды световой волны первичный источник S₀ можно заменить р системой эквивалентных ему вторичных

и сточников, расположенных на любой замкнутой поверхности S , такой, чтобы источник S₀ находился внутри поверхно­сти, а точка наблюдения P - снаружи. Для точечных источников в качестве поверхности S удобно выбирать сферу с центром, совпадающим с источником.

2. Волны вторичных источников когерентны и распространяются во всех направлениях. Световое поле, возникающее в результате их интерференции в про­странстве снаружи поверхности S, совпадает с полем реального источника Sо.

Если в качестве поверхности S выбрана волновая поверхность первичной волны (для точечного источника - сфера), тогда все вторичные волны будут иметь одина­ковую начальную фазу.

3. А мплитуда колебаний световой волны dE каж­дого вторичного источника (элемента поверхно­сти dS) в точке наблюдения P пропорцио­нальна площади этого источника dS , обратно пропорциональна расстоянию r от него до точ­ки наблюдения P и пропорциональна амплиту­де волны вторичного источника Ео, и некото­рой функции угла f (а)

dE = f (а)^E0dS. r

П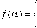 ро функцию угла f (а) можно сказать, что

1, при а = 0; 0, при аж/2,

и она монотонно убывает от 1 до 0 при изменении угла от 0 до П /2.