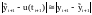Решение задачи Коши

Задача Коши или начальная задача для системы дифференциальных уравнений

, (1)

где – неизвестный вектор, – вектор-функция, состоит в нахождении решения системы, удовлетворяющего начальным условиям:

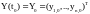(2)

Дифференциальное уравнение n-го порядка,

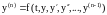
сводится к системе (1) с помощью подстановок:

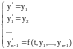
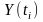При численном решении задачи Коши рассматривается последовательность точек , в общем случае, с переменной длиной шага . В каждой точке решение системы аппроксимируется вектором 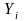, значение которого вычисляется по найденным значениям в предыдущих точках .

Погрешность аппроксимации, возникающая на каждом шаге, может быть описана следующим образом. Пусть рассматривается дифференциальное уравнение:

,

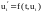где - точное решение уравнения, удовлетворяющее условию: 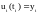. Локальной ошибкой дискретизации называется величина:

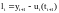
Численный метод имеет порядок точности p, если .

Рассмотрим методы решения задачи Коши на примере уравнения первого порядка

. (3)

Отметим, что все изложенные ниже методы применимы также при решении задачи Коши для системы уравнений (1), однако в этом случае все соотношения являются векторными.

Метод Эйлера для решения задачи Коши (3) описывается формулой:

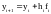, (4)

где . Метод Эйлера является методом первого порядка точности.

Два модифицированных метода Эйлера имеют второй порядок точности. Первый модифицированный метод Эйлера может быть представлен формулой:

(5)

Вторая модификация метода Эйлера (метод Эйлера-Коши) может быть описана формулой:

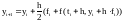(6)

В формулах (5), (6), по-прежнему, используется обозначение .

Метод Рунге–Кутта

Наиболее употребительный вариант метода Рунге-Кутта четвертого порядка может быть описан последовательностью формул:

(7)

Если решается задача Коши для системы уравнений, то величины y, f, k в формулах (4) – (7) являются векторами.

Оценка погрешности решения по правилу Рунге

Для оценки погрешности решения процесс решения повторяют дважды с разным шагом приращения аргумента: с шагом h и с шагом h/2. Пусть: – точное решение дифференциального уравнения, – численное решение, полученное с шагом h, – численное решение, полученное с шагом h/2, p - порядок метода, тогда погрешность более точного решения можно оценить, используя первую формулу Рунге:

(8)

Найденная оценка погрешности может быть использована для уточнения решения в соответствии со второй формулой Рунге:

(9)

Метод Рунге-Кутта-Фельберга позволяет оценивать погрешность решения без применения двойного пересчета. Формулы метода дают одновременно решения четвертого и пятого порядков точности. Разность этих решений служит оценкой погрешности более точного решения решения пятого порядка. Найденная оценка может использоваться для корректировки величины шага приращения аргумента.

Для нахождения нового значения неизвестной функции последовательно вычисляются величины:

(10)

Значение пятого порядка точности вычисляется как взвешенная комбинация величин :

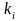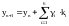(11)

Значения всех коэффициентов даны в таблице. Если в формуле (11) коэффициенты 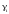заменить на коэффициенты , то получим решение четвертого порядка. Фактически на практике вычисляют решение пятого порядка и оценку погрешности:

(12)

Метод Адамса является многошаговым методом: для вычисления очередного значения неизвестной функции y_n+1 используется несколько предыдущих ее значений: y_n, y_n–1, y_n–2,… Применяется сетка значений аргумента с постоянным шагом приращения: h=t_n+1–t_n, n=0,1,… Общий вид формулы для m-шагового метода Адамса:

(13)

В этой формуле b_k, k=0,1,.., m – постоянные коэффициенты, а функция , как и прежде, представляет собой правую часть дифференциального уравнения. Если b₀=0, метод называется явным. В случае, когда 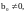неизвестная величина y_n+1 неявно входит в правую часть формулы (12); такой метод называется неявным. Порядок явного m-шагового метода Адамса равен m; порядок неявного метода равен m+1. Неявный метод является более точным и обладает более высокой устойчивостью. Однако применение неявного метода приводит к необходимости на каждом шаге приращения аргумента решать уравнение (12) относительно величины y_n+1. Эта трудность преодолевается в методе Предиктор–Корректор использованием на каждом шаге приращения аргумента двух формул: явной, называемой предиктором, и неявной, называемой корректором. Сначала вычисляется новое значение неизвестной функции с помощью менее точной явной формулы. Затем это значение уточняется с помощью формулы корректор; при этом для вычисления величины используется найденное значение Пара формул Адамса четвертого порядка для использования в методе Предиктор–Корректор имеет вид:

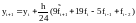
Оценка погрешности может быть найдена по формуле: