Теорема 1.1 (о существовании и единственности решения).

Если в уравнении

dy/dx = f(x,y)

функция f(x,y) непрерывна в прямоугольнике D:

x₀ -a ≤ x ≤ x₀ +a, y₀ - b≤ y ≤ y₀ + b,

и удовлетворяет в D условию Липшица:

| f(x,y₁) - f(x,y₂)| ≤ N|y₁ – y₂|,

где N – постоянная, то существует единственное решение y = y(x), x₀ -H≤ x ≤ x₀ +H, уравнения (1), удовлетворяющее условию y(x₀) = y₀, где

H< min(a, b/M, 1/N),

M = max f(x,y) в D.

Условие Липшица

| f(x,y₁) - f(x,y₂)| ≤ N|y₁ – y₂|

Может быть заменено несколько более грубым, но зато обычно легко проверяемым условием существования ограниченной по модулю частной производной f’_y(x,y) в области D.

Действительно, если в прямоугольнике D

|f’_y(x,y)| ≤ N,

То, пользуясь теоремой о конечном приращении. Получим

| f(x,y₁) - f(x,y₂)| =f’_y(x,ξ)|y₁ – y₂|,

где ξ – промежуточное между y₁ и y₂ значение. Следовательно, точка (x,ξ) лежит в D, поэтому

f’_y(x,ξ) ≤ N и | f(x,y₁) - f(x,y₂)| =N|y₁ – y₂|.

Доказательство теоремы существования и единственности.

Заменим дифференциальное уравнение

(3) dy/dx = f(x,y)

с начальным условием

(4) y(x₀) = y₀

эквивалентным интегральным уравнением (5)

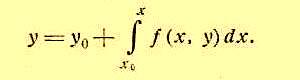
Действительно, если некоторая функция y = y(x) при подстановке обращает в тождество уравнение (3) и удовлетворяет условию (4), то, интегрируя тождество (3) и принимая во внимание условие (4), получим, что y = y(x) обращает в тождество и уравнение (5).

Строим ломаную Эйлера y = y_n(x), исходящую из точки (x₀,y₀) с шагом h_n=H/n на отрезке x₀ ≤ x ≤ x₀ +H , n – целое положительное число (совершенно аналогично доказывается существование решения на отрезке x₀ -H≤ x ≤ x₀). Ломаная Эйлера, проходящая через точку (x₀,y₀), не может выйти из области D при x₀ ≤ x ≤ x₀ +H (или x₀ -H≤ x ≤ x₀), так как угловые коэффициенты каждого звена ломаной по модулю меньше M.

Дальнейшее доказательство разобьем на три этапа:

1. Последовательность y = y_n(x) равномерно сходится.

2. Функция y =lim y(x) является решением интегрального уравнения (5).

3. Решение y(x) уравнения (5) единственно.

Метод последовательных приближений.

Предположим, что известно, решение y(x), которое приводится к y₀ при x=x₀. Это решение, очевидно, удовлетворяет соотношению

которое является интегральным уравнением, содержащим зависимую переменную под знаком интеграла. Будем рассматривать функцию y(x) как известную, тогда интегральное уравнение может быть решено методом последовательных приближений.

Допустим, что x лежит в интервале (x₀,x₀+h) и рассмотрим последовательность функций y₁(x), y₂(x), …,y_n(x), определенных следующим образом

Докажем теперь, что

1. с неограниченным ростом n, последовательность функций y_n(x) стремится к пределу, который является непрерывной функцией x;

2. предельная функция удовлетворяет дифференциальному уравнению;

3. найденное таким образом решение принимает значение y₀ при x=x₀ и является единственным непрерывным решением, которое обладает этим свойством.

Сначала докажем методом индукции, что если x лежит в рассматриваемом интервале, то |y_n(x)-y₀|≤b. Предположим, что |y_n+1(x)-y₀|≤b; отсюда следует, что |f{t, y_n-1(t)}| ≤M, поэтому

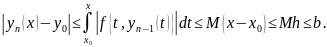
Очевидно,

Следовательно,

для всех значений n. Отсюда следует, что f{x, y_n(x)} ≤M при x₀<x<x₀+h.

Аналогично докажем, что

Если мы предположим, что то

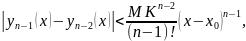
Откуда, согласно условию Липшица,

Так что

Неравенство, справедливое при n=1, действительно также для всех значений n. Аналогично можно доказать его справедливость при ,следовательно оно верно для |x-x₀|≤h.

Отсюда следует, что ряд

абсолютно и равномерно сходится при |x-x₀|≤h и более того – каждый член является непрерывной функцией x. Но

следовательно, предельная функция

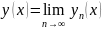
Существует и является непрерывной функцией x в интервале (x₀-h, x₀+h).

Теперь, если соотношение

верно, отсюда следует, что y(x) будет решение интегрального уравнения

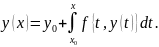
Законность перемены порядка интегрирования и перехода к пределу может быть доказана следующим образом:

где ξ_n не зависит от x и стремится к нулю, когда n стремится к бесконечности.

Функция f{t, y_n(t)} непрерывна в интервале x₀<t<x₀+h, следовательно

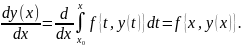
Отсюда следует, что предельная функция y(x) удовлетворяет дифференциальному уравнению; она также приводится к y₀, когда x принимает значение x_0.

Остается доказать, что это решение y(x) единственное. Предположим, что Y(x) является решением, отличным от y(x), удовлетворяющим начальному условию Y(x₀)=y₀ и непрерывным в интервале (x₀, x₀+h’), где h’≤h, а h’ таково, что условие,

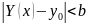
удовлетворяется для этого интервала. Тогда, поскольку Y(x) является решением данного уравнения, оно удовлетворяет интегральному уравнению

и следовательно,

Пусть n=1, тогда

и из условия Липшица следует, что

Аналогично при n=2

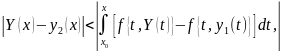
и в общем случае

откуда

для всех значений x в интервале (x₀, x₀+h’), поэтому полученное новое решение тождественно предыдущему. Следовательно, имеется только одно непрерывное решение дифференциального уравнения, которое удовлетворяет начальным условиям.