Построение действительных чисел с помощью сечений. Теоремы Вейерштрасса и Дедекинда. Представление действительных чисел десятичными, двоичными последовательностями.

Рассмотрим разбиение множества всех рациональных числе на два не пустые множества . Такое разбиение называется сечением, если выполняются условия:

1. каждое рациональное число попадает в одно, и только в одно из множеств А или А'.

2. каждое число а множества А меньше каждого число а' множества А'.

Множество А называется нижним классом сечения, множество А' – верхним классом. Сечение обозначаем через А│А’.

Из определения сечения следует, что всякое рациональное число, меньшее числа а нижнего класса, также принадлежит нижнему классу. Аналогично, всякое рациональное число, большее числа а' верхнего класса, и само принадлежит верхнему классу.

Сечения могут быть трех видов:

1. либо в нижнем классе А нет наибольшего числа, а в верхнем классе А' есть наименьшее число r;

2. либо в нижнем классе А имеется наибольшее число r, а в верхнем классе А' нет наименьшего;

3. либо ни в нижнем классе нет наибольшего числа, ни в верхнем классе – наименьшего.

В первых двух случаях сечение производится рациональным числом r (которое является пограничным между классами А и А') или это сечение определяет рациональное число r. В третьем случае пограничного числа не существует, сечение не определяет никакого рационального числа. Введем новые объекты – иррациональные числа, условившись говорить, что всякое сечение вида 3 определяет некоторое иррациональное число α.

Говоря о сечении рациональное число r включим в верхний класс.

Числа рациональные и иррациональные называются вещественные (или действительные).

Упорядочение области действительных чисел.

Два иррациональных числа α и β, определяемых соответственно сечениями А│А' и В│В', считаются равными в том и только в том случае, если эти сечения тождественны.

Свойства:

1. Для каждой пары вещественных чисел α и β имеет место одно, и только одно, из соответсвий:

α=β, α>β, β>α

2. Из α>β, β>γ следует, что α>γ

Теорема Дедекинда.

Для всякого сечения А│А' в области вещественных чисел существует вещественное число β, которое производит это сечение. Это число β будет 1) либо наибольшим в нижнем классе А, 2) либо наименьшим в верхнем классе А'.

Это свойство области вещественных чисел называют ее полнотой, а также – непрерывностью.

Доказательство.

Обозначим через А множество всех рациональных чисел, принадлежащих к А, а через А' – множество всех рациональных числе, принадлежащих к А'. Легко убедиться, что множества А и А' образуют сечение в области всех рациональных чисел.

Это сечение А│А' определяет некоторое вещественное число β. Оно должно попасть в один из классов А, А'; предположим, что β попадает, например, в нижний класс А, и докажем, что тогда осуществляется случай 1), а именно, β является в классе А наибольшим. В самом деле, если бы это было не так, то нашлось бы другое число α₀ этого класса, большее β. Вставим между α₀ и β рациональное число r:

α₀ >r>β;

r также принадлежит классу А и, следовательно, принадлежит классу А. Мы пришли к противоречию: рациональное число r, принадлежащее нижнему классу сечения, определяющего число β, больше этого числа! Этим доказано наше утверждение.

Аналогичное рассуждение показывает, что если β попадает в верхний класс А', то осуществится случай 2

Лемма Больцано-Вейерштрасса.

Из любой ограниченной последовательности всегда можно извлечь такую частичную подпоследовательность, которая сходиласьбы к конечному пределу.

Первая теорема Вейерштрасса.

Если функция f(x) определена и непрерывна в замкнутом промежутке [a,b], то на ограничена, т.е. существуют такие постоянные и конечные числа m и M, что

Доказательство проведём от противного: допустим, что функция f(x) при изменении x в промежутке [a,b] оказывается неограниченной.

В таком случае для каждого натурального числа n найдётся в промежутке [a,b] такое значение , что

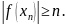
По лемме Больцано-Вейерштрасса, из последовательности 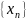можно извлечь частичную подпоследовательность 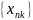сходящуюся к конечному пределу:

,

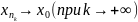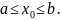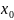Причем, очевидно, Вследствие непрерывности функции в точке , тогда должно быть и

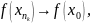а это невозможно, так как из 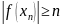следует, что

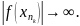
Полученное противоречие доказывает теорему.