2.1.3. Интерференция в тонком клине

П редставим себе, что плоская световая монохроматическая волна падает на тонкий клин, изготовленный из оптически прозрачного вещества, перпендикулярно к его основанию (см. рис. 2.4).

Клин настолько тонок, что отраженные лучи 1 и 3 идут практически параллельно друг другу вертикально вверх. Рассматриваемый сверху в отраженном свете клин представится нам «полосатым», причем световые полосы, чередуемые с темными полосами, будут параллельны острой кромке клина и будут находиться на равном расстоянии друг от друга - х.

Для двух соседних максимумов интерференции (двух соседних полос) можем записать:

2nd - (λ₀/2) = mλ₀

2n(d+h) - (λ₀/2) = (m+1)λ₀

Вычитая из одного равенства другое, получим:

2nh = λ₀

Т.к. h = х·tgφ ≈ х·φ,

то 2nхφ = λ₀.

Откуда следует:

х = λ₀/2nφ,

следовательно, расстояние между соседними светлыми (темными) полосами тем больше, чем тоньше клин. В пределе при φ → 0 поверхность клина представляется нам либо равномерно освещенной, либо равномерно затемненной.

Явление интерференции в оптически прозрачном клине нашло очень важное применение в технологии изготовления оптических линз. Ведь линза представляет своеобразный клин (хотя его поверхности не являются плоскими). Наблюдая за поверхностью линзы в отраженном свете можно по искривлению интерференционных полос обнаружить очень незначительные дефекты - неровности поверхности, неоднородность стекла.

2.1.4. Интерферометр Майкельсона

Рекордная точность в измерениях длины линейных отрезков (перемещений) достигается с помощью интерферометра Майкельсона, схема которого изображена на рис. 2.5.

П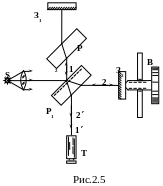 учок света от источника S падает на полупрозрачную пластинку P₁, покрытую тонким слоем серебра. Половина упавшего светового потока отражается пластиной Р₁ в направлении луча 1, половина проходит сквозь пластинку и распространяется в направлении луча 2. Пучок 1 отражается от зеркала З₁, и возвращается к P₁. Пучок 2, отразившись от зеркала З₂, тоже возвращается к пластине Р₁. Прошедшие через пластинку Р₁ лучи 1^/ и 2^/ когерентны между собой и имеют одинаковую интенсивность. Результат интерференции этих пучков зависит от оптической разности хода от пластинки Р₁ до зеркал 3₁ и З₂ и обратно. Луч 2 проходит толщину пластинки трижды, луч 1 - только 1 раз. Чтобы скомпенсировать возникающую за счет этого разную (вследствие дисперсии) для различных длин волн и различных температур оптическую разность хода, на пути луча 1 ставится точно такая, как Р₁, но не посеребренная пластинка Р₂.Тем самым уравниваются пути лучей 1 и 2 в стекле. Интерференционная картина наблюдается с помощью зрительной трубы Т. Вращая микрометрический винт В, можно плавно перемещать зеркало 3₂, тем самым можно изменять оптическую разность хода между лучами 1^/ и 2^/.

2n·∆L=2·N·λ₀/2 (max) , где n = 1.

Пусть в результате вращения микрометрического винта зеркало З₂ переместилось вдоль измеряемого отрезка на ∆L, при этом наблюдая в зрительную трубу, мы зафиксировали N интерференционных миганий. Нетрудно получить ∆L=N·λ₀/2. Откуда следует, что цена деления измерительного прибора составляет λ₀/2, т.е. для зеленого света она равна 0,27 мкм.