
- •Введение
- •1.Основные законы геометической оптики
- •Явление полного отражения.
- •2. Волновой характер световых волн.
- •2.1. Интерференция когерентных волн
- •2.1.1. Условия максимума и минимума интерференции когерентных волн
- •2.1.2. Интерференция при отражении света от тонких пластинок
- •2.1.3. Интерференция в тонком клине
- •2.1.4. Интерферометр Майкельсона
- •2.1.5. Интерференционные рефрактометры
- •2.2. Дифракция света
- •2.2.1. Принцип Гюйгенса-Френеля
- •2.2.2 Зоны Френеля
- •2.2.3 Дифракция Фраунгофера от щели.
- •2.2.4. Дифракционная решетка
- •2.2.5. Дифракция рентгеновских лучей
- •2.2.6. Голография
- •2.3. Поляризация света
- •2.3.1. Естественный и поляризованный свет
- •2.3.2. Способы получения поляризованного света
- •2.3.3 Закон Брюстера
- •2.3.4 Закон Малюса
- •2.3.5 Вращение плоскости поляризации
- •3. Взаимодействие электромагнитного излучения с веществом
- •3.1 Взаимодействие света с веществом
- •3.2. Классическая теория дисперсии
- •3.3 Тепловое излучение, его характеристика Абсолютно черное тело
- •3.4. Тепловое равновесие, закон Кирхгофа
- •3.5. Закономерности излучения абсолютно черного тела
- •3.6. Рассеяние света. Закон Рэлея
- •3.7 Поглощение света. Закон Бугера-Ламберта
- •3.8 Фотоэлектрический эффект и природа электромагнитного излучения
- •3.9.Эффект Комптона
- •4. Элементы квантовой механики
- •4.1 Гипотеза де Бройля (Волновые свойства микрочастиц. Дуализм материи)
- •4.2. Дифракция электронов. Опыт Дэвисона и Джермера
- •4.3. Соотношение неопределенностей
- •4.4. Волновая функция. Уравнение Шредингера
- •4.5 Операторы физических величин. (Самостоятельно)
- •Электрон в «потенциальной яме» Квантование энергии
- •(Теория атома водорода по Бору. Модель атома Резерфорда. Линейчатый спектр атома водорода. Строение атома. Постулаты Бора. Спектр атома водорода по Бору. Опыт Франка и Герца.)
- •5.Теория атома водорода по бору
- •5.1.Модель атома Резерфорда
- •5.2. Линейчатый спектр атома водорода
- •5.3. Строение атома. Постулаты Бора
- •5.4. Спектр атома водорода по Бору
- •5.5. Опыт Франка и Герца
- •Лекция 13
- •6. Физика атомного ядра
- •6.1.Состав атомного ядра и энергия связи ядра Законы радиоактивных превращений
- •6.2.Кинетика естественного радиоактивного распада
- •6.3. Ядерные реакции и их классификация
- •6.4.Управляемая реакция деления ядер
- •6.5. Использование ядерных превращений
- •6.5.1.Ядерная энергетика
- •6.5.2.Атомная бомба
- •6.5.3.Реакция синтеза атомных ядер
- •Библиографический список
4.2. Дифракция электронов. Опыт Дэвисона и Джермера
Пучок монохроматических электронов из электронной пушки Р падал на поверхность кристалла Никеля (рис.4.1). Рассеянные от кристалла электроны улавливались приемником, который мог перемещаться так, чтобы улавливать электроны, рассеиваемые под различными углами.
В процессе измерений было установлено, что распределение потока отраженных электронов согласуется с формулой Вульфа - Брэггов:
![]()
Т .е.
движущиеся электроны проявляют волновые
свойства; причем полученное из этой
формулы значение
хорошо совпадает с длиной волны де
Бройля для электронов, имеющих данную
скорость. Этот результат представляет
собой прекрасное доказательство
правильности идеи де Бройля.
.е.
движущиеся электроны проявляют волновые
свойства; причем полученное из этой
формулы значение
хорошо совпадает с длиной волны де
Бройля для электронов, имеющих данную
скорость. Этот результат представляет
собой прекрасное доказательство
правильности идеи де Бройля.
Впоследствии дифракционные явления были обнаружены для нейтронов, протонов, атомных и молекулярных пучков. На частицы вещества переносится связь между полной энергией ε частицы и частотой ν волн де Бройля: ε = hν, т.е это универсальное соотношение, справедливое как для фотонов, так и для любых других микрочастиц.
4.3. Соотношение неопределенностей
Классическая теория считает возможным постановку эксперимента, из которого можно одновременно и с кокой угодно точностью определить координату частицы х и её импульс mv (или скорость v). Однако, немецкий физик /ФРГ/ Гейзенберг показал, что в области микромира это не достижимо. Рассмотрим один из мысленных опытов Гейзенберга.
Пусть требуется
определить в одном и том же опыте
координату и импульс электрона,
движущегося вдоль оси х. Самый точный
способ определения расстояния - оптический
- с помощью интерферометра Майкельсона.
В данном случае точность измерения
координаты
![]() достигает длины волны излучения,
используемого в интерферометре
.
По Эйнштейну свет представляет собой
поток фотонов, каждый из которых имеет
импульс Рф=h/
.
При столкновении фотона с электроном
электрон может получить дополнительный
импульс, следовательно, импульс электрона
может измениться на величину порядка
Рф.
Составим произведение:
достигает длины волны излучения,
используемого в интерферометре
.
По Эйнштейну свет представляет собой
поток фотонов, каждый из которых имеет
импульс Рф=h/
.
При столкновении фотона с электроном
электрон может получить дополнительный
импульс, следовательно, импульс электрона
может измениться на величину порядка
Рф.
Составим произведение:
![]()
Итак:
![]()
Это- соотношение неопределенностей Гейзенберга.
Т.е. произведение
погрешностей одновременного измерения
координаты и импульса электрона не
может быть меньше постоянной Планка h.
Если мы
стремимся уменьшить погрешность
измерения координаты
![]() ,
то необходимо использовать жесткое
излучение (с малым
),
но это приведет к увеличению
,
то необходимо использовать жесткое
излучение (с малым
),
но это приведет к увеличению
![]() и
и
![]() .
.
Лекция 11
(Волновая функция. Уравнение Шредингера. Операторы физических величин. Электрон в «потенциальной яме». Квантование энергии.)
4.4. Волновая функция. Уравнение Шредингера
Невозможность одновременного точного нахождения координаты и импульса (координаты и скорости) частиц микромира заставило отказаться от классической механики в применении к рассматриваемому объекту, снять задачу о точном знании положения частиц и перейти к определению вероятности нахождения частицы в том или ином месте пространства. В результате была разработана специальная механика, изучающая поведение и состояния частиц микромира,- квантовая механика.
Одной из главных
задач квантовой механики является
нахождение волновой функции
= x,y,z,t).
Произведение квадрата модуля волновой
функции на элемент объема пространства
2dV
физически толкуется как вероятность
того, что действие частицы будет
обнаружено в элементе объема dV.
Следовательно, 2
толкуется как плотность вероятности
обнаружения частицы (электрона). Сумма
величин 2dV
по всему пространству, т.е.
![]() есть вероятность обнаружения частицы
где бы то ни было в пространстве. Но т.к.
частица существует, следовательно,
-функция должна удовлетворять условию:
есть вероятность обнаружения частицы
где бы то ни было в пространстве. Но т.к.
частица существует, следовательно,
-функция должна удовлетворять условию:
![]() =1 - УСЛОВИЕ НОРМИРОВКИ.
=1 - УСЛОВИЕ НОРМИРОВКИ.
Если известна -функция, описывающая состояние, то вероятности всевозможных процессов определяются однозначно.
Наличие волновых свойств у частиц микромира наводит на мысль о том, что к частицам должно быть применимо волновое уравнение, из которого как раз и может быть найдена волновая функция :
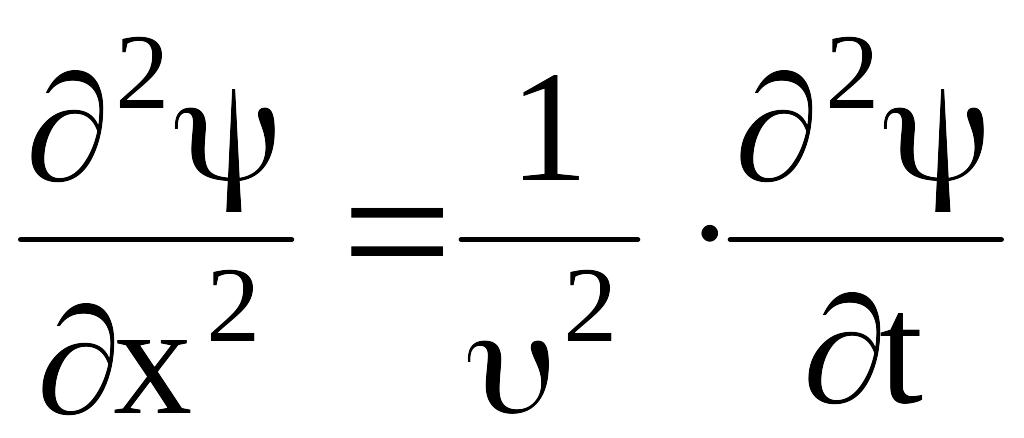 (4.5)
(4.5)
где - скорость распространения волны де Бройля. Удовлетворяющая этому дифференциальному уравнению функция (x,t) имеет вид:
(x,t) = 0 cos (ωt – kx) (4.6)
Беря вторую производную по времени от -функции, заданной уравнением (4.6), получим:
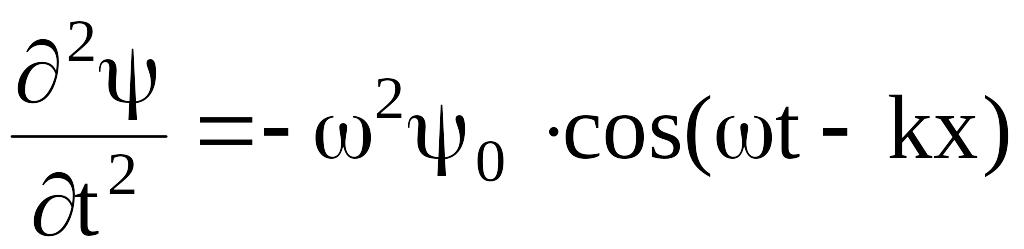 (4.7)
(4.7)
Подставляя (4.7) в
(4.5), находим:
![]()
или поскольку
![]() ,
,
то
![]() (4.8)
(4.8)
В соответствии с гипотезой де Бройля заменим в выражении (4.8) величину =h/P:
![]() (4.9)
(4.9)
Т.к.
![]()
![]()
где Е и ЕП - соответственно полная и потенциальная энергия частицы, то
![]()
Это - СТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА.
