10. Линейная модель авторегрессионного процесса первого порядка
В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков должна быть устранена.
Устранить автокорреляцию остатков модели регрессии можно с помощью включения в модель автокорреляционного параметра, однако на практике данный подход реализовать весьма затруднительно, потому что оценка коэффициента автокорреляции является величиной заранее неизвестной.
Авторегрессионной схемой первого порядка называется метод устранения автокорреляции первого порядка между соседними членами остаточного ряда в линейных моделях регрессии либо моделях регрессии, которые можно привести к линейному виду.
На практике применение авторегрессионной схемы первого порядка требует априорного знания величины коэффициента автокорреляции. Однако в связи с тем, что величина данного коэффициента заранее неизвестна, в качестве его оценки рассчитывается выборочный коэффициент остатков первого порядка ρ1.
Выборочный коэффициент остатков первого порядка ρ1 рассчитывается по формуле:
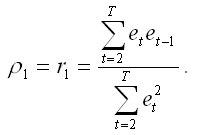
В общем случае коэффициент автокорреляции порядка l рассчитывается по формуле:
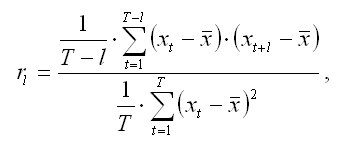
где l – временной лаг;
T – число наблюдений;
t – момент времени, в который осуществлялось наблюдение;
x – среднее значение исходного временного ряда.
11. Обобщенный метод наименьших квадратов
Обобщённый
метод наименьших квадратов —
метод оценки параметров регрессионных
моделей,
являющийся обобщением классического метода
наименьших квадратов.
Обобщённый метод наименьших квадратов
сводится к минимизации «обобщённой
суммы квадратов» остатков регрессии —
, где 
—
вектор остатков, 
—
симметрическая положительно определенная
весовая матрица. Обычный МНК является
частным случаем обобщённого, когда
весовая матрица пропорциональна
единичной.
Необходимо отметить, что обычно обобщённым методом наименьших квадратов называют частный случай, когда в качестве весовой матрицы используется матрица, обратная ковариационной матрице случайных ошибок модели.
Известно,
что симметрическую положительно
определенную матрицу можно разложить
как 
,
где P- некоторая невырожденная квадратная
матрица. Тогда обобщённая сумма квадратов
может быть представлена как сумма
квадратов преобразованных (с помощью
P) остатков 
.
Для линейной
регрессии 
это
означает, что минимизируется величина:
где 
,
то есть фактически суть обобщённого
МНК сводится к линейному преобразованию
данных и применению к этим данным обычного
МНК. Если в качестве весовой
матрицы
используется
обратная ковариационная
матрица 
случайных
ошибок 
(то
есть 
),
преобразование P приводит к тому, что
преобразованная модель удовлетворяет
классическим предположениям
(Гаусса-Маркова), следовательно оценки
параметров с помощью обычного МНК будут
наиболее эффективными в классе линейных
несмещенных оценок. А поскольку параметры
исходной и преобразованной модели
одинаковы, то отсюда следует
утверждение — оценки ОМНК являются
наиболее эффективными в классе линейных
несмещенных оценок (теорема Айткена).
Формула обобщённого МНК имеет вид:
Ковариационная матрица этих оценок равна:
