6. Компоненты динамического ряда, аддитивная и мультипликативная модели динамичного ряда

Динамический ряд ( временной ряд, ряд динамики) – совокупность последовательных значений некоторого показателя, характеризующих его изменение в дискретном времени

В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется адитивной моделью временного ряда. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда. Основная задача исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.

• обобщенная аддитивная модель динамического ряда

• о бобщенная мультипликативная модель динамического ряда

7. Автокорреляция уровней динамического ряда. Автокорреляционная функция.

Автокорреляция

● Корреляционную зависимость между

последовательными уровнями временного ряда

называют автокорреляцией уровней ряда.

Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Коэффициент корреляции имеет вид:

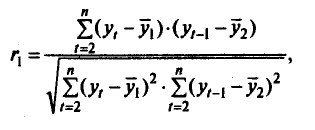
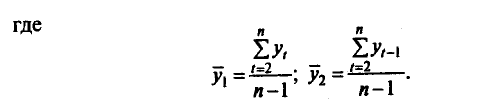
Коэффициент автокорреляции первого порядка измеряет зависимость между соседними уровнями ряда t и t-1, т.е. при лаге 1.

Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков.

Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Некоторые авторы считают целесообразным для обеспечения статистической достоверности коэффициентов корреляции использовать правило – максимальный лаг должен быть не больше (n/4).

Отметим два важных свойства коэффициента автокорреляции.

Во-первых, он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной (или близкой к линейной) связи текущего и предыдущего уровней ряда. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю.

Во-вторых, по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда.

Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага называется коррелограммой.

Анализ автокорреляционной функции и графика можно выявить структуру ряда. Если наиболее высоким оказался коэффициент автокорреляции 1го порядка, то ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент порядка – то содержит циклические колебания с периодичностью в моментов времени. Если ни один из коэффициентов не является значимым, то 2 предположения: 1. ряд не содержит тенденции и циклических колебаний, 2. ряд содержит сильную нелинейную тенденцию.

Вопрос № 8

От сезонных и циклических колебаний следует отличать единовременные изменения характера тенденции временного ряда, вызванные структурными изменениями в экономике или иными факторами. В этом случае, начиная с некоторого момента времени t, происходит изменение характера динамики изучаемого показателя, что приводит к изменению параметров тренда, описывающего эту динамику. Тренд это среднее поведение колебаний. Временной ряд это последовательность статистических данных, собранных в определенный момент времени. Существует несколько подходов к анализу структуры временных рядов, содержащих сезонные или циклические колебания. 1 подход: построение аддитивной или мультипликативной модели временного ряда. Аддитивная модель имеет вид x(t)=F(t)+P(t)+E(t), где F(t)-трендовая компонента, P(t)-периодическая составляющая от тенденции(или сезонная компонента) и E(t)- случайные ошибки. Мультипликативная модель имеет вид x(t)=F(t)*(t)(кси). (t) находится как квадрат ошибок. Если временной ряд плохо прогнозируется, то целесообразно прологарифмировать данные и проделать построение модели снова.

Вопрос №9

Для того, чтобы определить стили тренда выписывается Автокорреляционная функции (АКФ). Значения коэф. Корреляции должны быть одного знака и достаточно велики. Если же нет, то можно заложить квадратическую или кубическую функцию. Если коэф. Корреляции приближается к 0, то возможно стационарное изучение процесса. Построение аналитической функции при моделировании тренда, в любой задаче по эконометрике на временные ряды, называют аналитическим выравниванием временного ряда и в основном применяются функции: линейную, степенную, гиперболичческую, параболическую и т.д.

Параметры тренда определяются как и в случае линейной регрессии методом наименьших остатков, где в качестве независимой переменной выступает время, а в качестве зависимой переменной – уровни временного ряда. Критерием отбора наилучшей формы тренда служит наибольшее значение коэффициента детерминации, критерии фишера и Стьюдента.

Автокорреляция в остатках – корреляционная зависимость между значениями остатков за текущий и предыдущие моменты времени. Для определения автокорреляции остатков используется критерий Дарбина – Уотсона: 2*(1-автокорреляция по последним ошибкам). Далее определяем в какой зоне на автокорреляционной прямой находится наше значение. Границы на данной прямой находятся по значениям в таблице, а также по значениям коэффициента корреляции. Может оказаться, что значение находится в зоне неопределенности, т.е. при таких результатах сложно точно сказать есть ли автокорреляционная зависимость. Возможно, что автокорреляция прослеживается, либо ее нет.