3. Множественная линейная регрессия. Корреляционная матрица.

Множественная линейная регрессия является обобщением парной линейной регрессии на несколько объясняющих переменных. При выполнении предпосылок Гаусса-Маркова оценки параметров уравнения множественной линейной регрессии, полученные методом наименьших квадратов, обладают свойствами несмещенности, эффективности и состоятельности. Статистическая значимость коэффициентов и качество подбора уравнения проверяются с помощью распределений Стьюдента и Фишера. Коэффициент при объясняющей переменной показывает, на сколько единиц изменится зависимая переменная, если объясняющая вырастет на одну единицу при фиксированном значении остальных объясняющих переменных. В случае множественной регрессии дополнительно предполагается отсутствие мультиколлинеарности объясняющих переменных.

Модель множественной регрессии строится в том случае, если коэффициент множественной корреляции показал наличие связи между исследуемыми переменными.

Общий вид линейной модели множественной регрессии:

где y – значение i-ой результативной переменной, i=1,n;

x1…xN – значения факторных переменных;

a,b1…bN – неизвестные коэффициенты модели множественной регрессии;

Е – случайные ошибки модели множественной регрессии.

При построении нормальной линейной модели множественной регрессии учитываются пять условий:

1) факторные переменные x1…xN – неслучайные или детерминированные величины, которые не зависят от распределения случайной ошибки модели регрессии a,b1;

2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:

3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:

4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т.е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):

5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2: εi~N(0, G2).

Корреляционная матрица — это квадратная таблица, в которой на пересечении соответствующих строки и столбца находится коэффициент корреляции между соответствующими параметрами.  В MS Excel для вычисления корреляционных матриц используется процедура Корреляция из пакета Анализ данных. Процедура позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами.

4. Метод включения факторов, метод исключения факторов

Методы построения уравнения множественной регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии к разным методам:

1) метод исключения (отсев факторов из полного его набора);

2) метод включения (дополнительное введение фактора);

3) шаговый регрессионный анализ (исключение ранее введенного фактора).

Каждый из этих методов по-своему решает проблему отбора факторов, давая в целом близкие результаты.

Метод пошагового включения переменных состоит в выборе из всего возможного набора факторных переменных именно те, которые оказывают существенное влияние на результативную переменную.

Метод пошагового включения осуществляется по следующему алгоритму:

1) из всех факторных переменных в модель регрессии включаются те переменные, которым соответствует наибольший модуль линейного коэффициента парной корреляции с результативной переменной;

2) при добавлении в модель регрессии новых факторных переменных проверяется их значимость с помощью F-критерия Фишера. При том выдвигается основная гипотеза о необоснованности включения факторной переменной xk в модель множественной регрессии. Обратная гипотеза состоит в утверждении о целесообразности включения факторной переменной xk в модель множественной регрессии. Критическое значение F-критерия определяется как Fкрит(a;k1;k2), где а – уровень значимости, k1=1 и k2=n–l – число степеней свободы, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров. Наблюдаемое значение F-критерия рассчитывается по формуле:

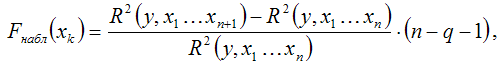
где q – число уже включённых в модель регрессии факторных переменных.

При проверке основной гипотезы возможны следующие ситуации.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл›Fкрит, то основная гипотеза о необоснованности включения факторной переменной xk в модель множественной регрессии отвергается. Следовательно, включение данной переменной в модель множественной регрессии является обоснованным.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл≤Fкрит, то основная гипотеза о необоснованности включения факторной переменной xk в модель множественной регрессии принимается. Следовательно, данную факторную переменную можно не включать в модель без ущерба для её качества

3) проверка факторных переменных на значимость осуществляется до тех пор, пока не найдётся хотя бы одна переменная, для которой не выполняется условие Fнабл›Fкрит.

Вопрос №5

Гомоскедастичность остатков (ошибок) означает, что дисперсия остатков одна и та же для каждого значения Xi. Гетероскедастичность - дисперсия объясняемой переменной (а следовательно, и случайных ошибок) не постоянна. Тест Гольдфельда- Куандта проверяет, зависит ли дисперсия случайных остатков от какого- то конкретного показателя. Тест применяется, как правило, когда есть предположение о прямой зависимости дисперсии ошибок от величины некоторой объясняющей переменной, входящей в модель. Например, с помощью этого теста можно проверить зависят ли E(остатки) от изменения фактора х1. Для данного теста нужно упорядочить (сделать сортировку) все данные (у, х1,х2) по возрастанию какого – либо фактора(например, х1). Далее необходимо разделить все данные на 3 блока (причем 1 и 3 части должны быть равны) и с помощью метода наименьших квадратов находить показатели. Такие как коэффициент детерминации (R^2) и распределение Фишера (F). Данные показатели покажут отклоняются ли ошибки от изменения фактора. Если да, то они гетероскедастичны, если нет, то гомоскедастичны. Для полноты наблюдения можно проверить таким образом на гетеро и гомоскедастичность и другие факторы (например, у). Проверка на гетеро и гомоскедастичность может осуществляться и с помощью теста ранговой корреляции Спирмана. Ранг – порядок данных, расположенных либо в порядке возрастания, либо в порядке убывания. Данный тест показывает имеется ли влияние фактора(например,х1) на величину ошибок. При выполнении теста необходимо найти модули фактора и сделать сортировку х1 по убыванию вместе с модулями данного фактора и сортировку рангов х1. Найти разницу между получившимися значениями. Тест Спирмана = ( Коэф. Корреляции * (n-2)^0,5)/((1-Коэф коррел^2)^0,5). Данное значение сравнивается с табличным и если оно больше, то ошибки гетероскедастичны.