Вопрос 36: Линейные интегрирующие цепи.

Применяются для интегрирования во времени электрических сигналов.

_t

U_вых (t) = U_вых (0) + k ∫ U_вх (t) dt

⁰

k – коэффициент пропорциональности.

В составе выходного сигнала есть постоянная составляющая.

U_вых (0) = 0

_t

U_вых (t) = (1 / C) ∫ i (t) dt

⁰

i = (U_вых – U_вх) / R

_{t t}

U_вых (0) = 0

(1 / C) ∫ (U_вых – U_вх) / R dt = – (1 /RC) ∫ (U_вых – U_вх) dt

^{0 0}

| U_вых| << | U_вх|

_t

U_вых (t) = (1 / RC) ∫ U_вх / R dt – выражение для интегрирования входного сигнала.

⁰

Для того, чтобы цепь была интегрирующей, нужно U_вых (t) было мало, а так как U_вых зави­сит от τ, то возрастанием τ приводит к возрастанию точности интегрирования. Т.о., необходимо 2 условия: U_вых (t) должно быть мало и τ должно быть большим. Рассмотрим прохождение прямоугольного импульса через RC – цепочку. Пусть имеется прямоугольный импульс.

U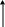 _вых

_tи

Допустим, в момент t = 0 U_вых = U_с = 0,

U_вых (0) = U_вх (1 – e^{t / τ}), τ = RC.

Разложим e^{t / τ} в ряд Маклорена.

f(x) = f (0) + (x / 1!) f ‘ (0) + (x² / 2!) f ‘‘ (0) +(x³ / 3!) f ‘‘‘ (0) +…

U_вых (t) = U_вх (1 – 1 + t / τ + (1 / 2!) (t / τ)² + …+ (1 / n!) (t / τ)ⁿ)

U_вых (t) = U_вх (t / τ) (1 – t / 2τ)

U_вх (t / τ) – при идеальном интегрировании

U_вх (t² / 2τ²) –ошибка интегрирования

γ – относительная погрешность интегрирования.

γ = δ / U_вх (t_и / 2τ)

Чтобы γ = 0.01 (1%), тогда t_и / τ = 0.02, т.е. τ = RC → RC ≥ 50t_и.

В дальнейшем при t > t_и должно быть постоянно ( ), но через 2τ ÷ 3τ станет 0.

Импульс растягивается по ширине и меняет свою форму. Легко рассчитать такую цепь. И погрешность 1%.

Для серии импульсов:

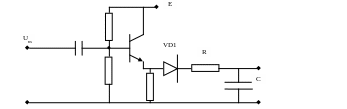
Диод предотвращает разряды. Для создания качественного интегрирования используют ОУ, в котором U_вых, благодаря глубокой ОС, практически не зависит от коэффициента усиления.

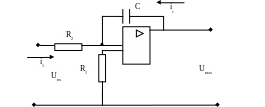
_tи

U_c = U_вых = (1 / C) ∫ i_с dt

⁰

i = U_вх / R, i = – i_с

Если U_вх = const, тогда

_tи

U_вых = – (1 / RC) ∫ U_вх dt = – (U_вх / RC) t_и

⁰

При подаче на вход интегратора скачка напряжения, выходное напряжение растет по экс­понентациальному закону.

U_вых (t) = – U_вх * k (1 – e^-t/τc); τ_c = k*R*C

Выходное напряжение такого интегратора в k раз больше, чем в простой цепи. γ = t_и / 2τ.

Значит, относительная погрешность в k раз упадет.

С ключом – аналоговое запоминающее устройство.

Заряд, существовавший на конденсаторе, в момент отключения мало меняется с течением времени. Это режим хранения. Интегратор выступает как запоминающее устройство. В этом режиме конденсатор разряжается только за счет собственной утечки, либо входного тока (ток нА). Эти параметры ограничивают минимальную длительность хранения сиг­нала. Можно использовать интегратор – сумматор, интегрирующий несколько сигналов от раз­нообразных источников.

Вопрос 37: Дифференцирующие цепи (пассивные rc и на оу (активные)).

Для преобразования импульсов напряжения U_вх (t) в сигнал U_вых (t), изменяющийся по за­кону U_вых (t) = m d U_вх / dt, где m – постоянная. Простейшая дифференциальная цепь:

U_вых (t) = i * R = C dU_c / dt *R = RC dU_c / dt.

U_вых (t) = RC (dU_вх / dt – dU_вых / dt)

При условии, что dU_вх / dt >> dU_вых / dt, тогда U_вых (t) = RC dU_вх / dt. Следовательно, погрешность, вносимая в цепь, dU_вых / dt. Оценим эту величину. Продиф­ференцируем это выражение.

dU_вых / dt = RC d² U_вх / dt²

d² U_вых / dt² = 0

U_вых (t) = RC (dU_вх / dt – d² U_вх / dt²)

Для улучшения дифференцирования необходимо, чтобы dU_вх / dt >> d² U_вх / dt². τ = RC должно быть как можно меньше. При дифференцировании импульса активная ширина спектра ограничена частотой f_гр. Для дифференцирования синусоидального сигнала необходимо соблюсти условие: ωRC ≤ 0.25. Если это условие выполняется при ω = 2π f_гр, то оно будет выполняться и для всех других частот спектра. Т.о., требования к постоянной времени дифференциальной цепи 2π f_гр RC = 0.25. При t_фронта = f_среза (сигнал ), следовательно, f_гр = k₀ / t_фронта, k₀ = 0.2÷0.4. Тогда, RC = 0.25 t_фронта / 2π k₀ = 0.25 t_фронта / 2π*0.4 = 0.1 t_фронта Постоянная времени должна быть в 10 раз меньше длительности фронта дифференциаль­ного импульса. Недостатки простейших дифференциальных цепей: уровень сигнала на выходе очень мал; существенные погрешности преобразования. Применение ОУ устраняет этот недостаток.

Дифференциальный усилитель:

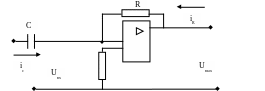
Если на вход подано входное напряжение U_вх, то в связи малого отличия потенциала не­инвертирующего входа от 0, то U_вх будет полностью приложено к емкости и вызовет по­явление тока заряда. i_с = C dU_вх / dt i_с + i_R = 0 (по Кирхгофу) i_с = – i_R => i_R = – C dU_вх / dt; U_вых (t) = i_R * R = – RC dU_вх / dt. Недостаток схемы: она может самовозбуждаться из-за спада коэффициента усиления на высоких частотах и из-за дополнительных связей, вносимых RC – цепью ОС и на высоких частотах могут усилиться собственные шумы и исказить сигнал.

Здесь спад

Поэтому на практике применяют модифицированную схему, которая имеет вид:

На частотах до ω₁ = 1 / C₁R₂ сигнал дифференцируется, от частоты ω₁ до ω₂ усиливается, а от ω₂ = 1 / C₂R₁ сигнал интегрируется.

При дифференцировании однополярного импульса на выходе двухполярные импульсы.

Длительность выходного импульса много меньше длительности дифференциального им­пульса. На их основе строятся укорачивающие цепи.

U_с

U_вх

Пусть на входе идеальный прямоугольный импульс. Конденсатор начинает заряжаться U_c = U_вх (1 – e^–t/RC), зарядный ток протекает через резистор, создает экспоненциальный импульс. U_вых = i * R = U_вх e^–t/RC. Затухает задолго до окончания действия входного им­пульса. После окончания входного импульса равновесие в цепи нарушается, происходит разряд конденсатора через резистор. Выходной импульс имеет обратную полярность.

t_u' = 2.3 τ = 2.3 RC

RC = τ = t_u' / 2.3

τ_диф ≤ 0.1 t_и

τ_интег ≥ 50 t_и

Если нужно ещё больше укоротить импульс, то уменьшиться выходное напряжение и со­противление нагрузки. Лучше уменьшить емкость. В реальной цепи сколь угодно короткий импульс получить нельзя. Часто стоит обратная задача – пропустить импульс через RC – цепь с минимальными по­терями.

К1

К2

К3

Э та задача при проектировании многокаскадных усилителей с импульсными сигналами.

U_вх

t

При подаче скачка на вход конденсатора будет скачок тока i = U_вх / R.

Появляется скачок тока на выходе U_вых = i * R = U_вх

U_вых = U_вх e^–t/RC

∆А = λ (t) = t_и / τ – спад вершины; τ >> t_и

U_вых

∆А

U_вх

t

Зная параметры входного импульса, можно так подобрать RC, чтобы обеспечить мини­мально допустимые искажения.