11. Гиперболические функции

О. Функции гиперболического синуса и гиперболического косинуса комплексного аргумента определены тождествами

С. Для всех справедливы тождества

С. Функции sh z и ch z определены и непрерывны на всей комплексной плоскости.

С. Нули функций sh z и ch z лежат на мнимой оси, более того

О. Функции гиперболического тангенса th z и гиперболического котангенса cth z определены тождествами

C. функция th z непрерывна на всей комплексной плоскости за исключением точек z=iπ(k+1/2), k принадлежит Z. Функция cth z непрерывна на всей комплексной плоскости за исключением точек z=iπk k принадлежит Z.

11. Логарифмическая функция

О. Логарифмической функцией комплексного аргумента z называется функция обратная к

В силу определения.

С. Логарифмическая функция комплексного аргумента определена на всей комплексной плоскости кроме z=0 и принимает конечное число значений

C. Для всех z₁, z₂ принадлежащих С отличных от нуля, имеет мест тождество Ln(z₁*z₂)=ln z₁ +ln z₂

11. Обратная показательная функция

11. Обратные тригонометрические и гиперболические функции.

11. Гармонические функции

Уравнение Лапласа: ∆U≡U_xx+U_yy+U_zz=0, в полярный координатах

Функции U=U(x,y) на плоскости и U=U(x,y,z) в пространстве, имеющие непрерывные частные производные второго порядка и удовлетворяющие, соответственно, уравнению Лапласа в некоторой области D, называются гармоническими в этой области. Простейшими примерами гармонических функций являются линейные функции: U = ах + by + с на плоскости и U = ax + by + cz + d в пространстве.

11. Интеграл фкп, его свойства и вычисление.

Пусть ФКП f(z) определена в точках не самопересекающейся дуги (l)=AB, расположенной в z–плоскости. Дуга (l) ориентирована от точки A к точке B, причем точка A соответствует z=z_A, точка B z=z_B.

Рассмотрим произвольное разбиение дуги AB системой точек 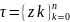такое, что z₀=z_A, z_n=z_B и z₁,z2, … ,z_n упорядочены по длине дуги от точки z_a до конечной точки разбиения z_B.

Выберем на дуге AB произвольную систему точек так, чтобы точка ξ лежала на дуге между точками z_k и z_k+1 (см. рисунок). Сумма , где , называется интегральной суммой функции f(z) по дуге (l), соответствующей разбиению τ и выбору точек системы ξ, ее значение зависит от разбиения τ и выбора точек ξ. Обозначим – диаметр разбиения.

Интегралом ФКП f(z) по дуге (l) называется число (вообще говоря, комплексное число), обозначаемое и равное пределу интегральной суммы функции f(z) при , независимое от разбиения τ и выбора точек системы ξ, т.е.

. (1)

Доказано (см. [2]), что для непрерывной на дуге ФКП и кусочно-гладкой дуги интеграл (1) существует. Впредь будем предполагать эти условия выполненными.

СВОЙСТВА интеграла

Cвойства криволинейных интегралов 2 рода (по координатам) переносятся на интеграл ФКП (1).

1) (аддитивность по функции);

,(k-const) (однородность);

– смена знака значения интеграла при изменении ориентации дуги.

2)

3)Если дуга (l) – контур, т.е. z_A=z_B, то интеграл ФКП по контуру (l) обозначается . Если , то интеграл называется несобственным интегралом.

4) Оценка интеграла ФКП проводится по формуле

если f(z) ограничена на (l), т.е. существует число M>0 такое, что на (l); S – длина дуги (l).

5) Если дуга (l) задана параметрически т.е. то вычисление интеграла (1) проводится с помощью вычисления соответствующих криволинейных интегралов (2) сведением к определенному интегралу с использованием уравнений дуги:

. (4)

6) , так как на окружности f имеем и . (5)

Определенный интеграл с переменным верхним пределом, формула Ньютона-Лейбница. Интегрирование по частям и замена переменной в определенном интеграле.