Завдання №5

Розв’язати задачу Коші для системи ДР на основі загального розв’язку. Для однорідної системи стала h = 0, а для неоднорідної системи h = 1.

1 Щоб одержати диференціальне рівняння для однієї з невідомих функцій або , вибираємо одне з рівнянь системи і диференціюємо його.

Тепер скористаємося ДР для похідної іншої невідомої функції

В останньому рівнянні є інша невідома . Її можна виразити через вибрану невідому функцію і її похідну за допомогою вибраного ДР

Останнє рівняння переписуємо у стандартному вигляді (2.23)

Ми одержали ЛНДР другого порядку зі сталими коефіцієнтами і правою частиною спеціального вигляду.

2 Спочатку знаходимо загальний розв’язок ЛНДР за прикладом 3.3.

Таким чином,

З вибраного ДР знаходимо другу невідому функцію:

В результаті одержуємо загальний розв’язок системи ЛДР

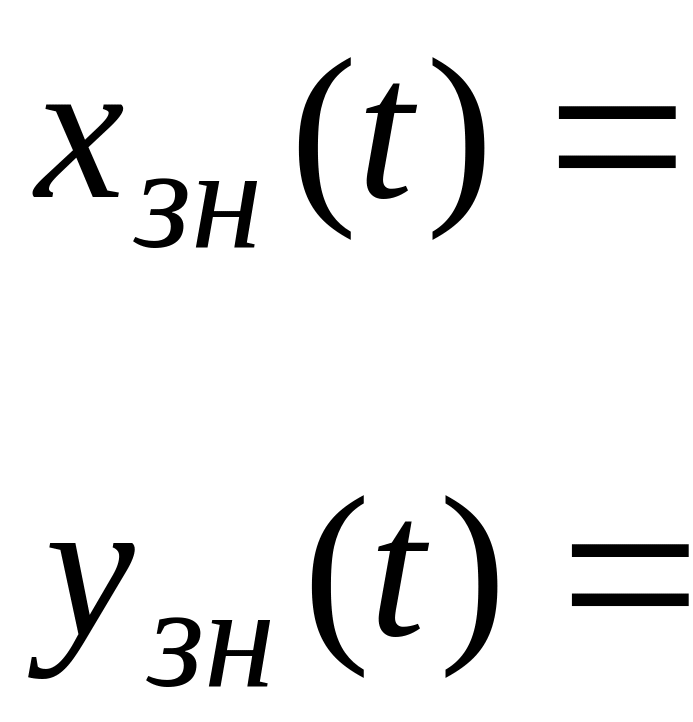
Для розв’язання задачі Коші прирівнюємо і і одержуємо систему для :

Розв’язок цієї системи підставляємо в і і одержуємо розв’язок задачі Коші