Українська державна академія залізничного транспорту

ФАКУЛЬТЕТ УПРАВЛІННЯ ПРОЦЕСАМИ ПЕРЕВЕЗЕНЬ

КАФЕДРА ВИЩОЇ МАТЕМАТИКИ

Диференціальні рівняння

Частина І

Завдання і методичні вказівки

до контрольної роботи з розділу дисципліни “Вища математика” для студентів загально-технічних спеціальностей

Виконав студент .

групи________________

_____________________

_____________________

Варіант № ___________

Перевірив____________

____________________

Харків – 2006

Завдання і методичні вказівки призначені для студентів загально-технічних спеціальностей безвідривної форми навчання. Розглянуті і рекомендовані до друку на засіданні кафедри вищої математики УкрДАЗТ, протокол № 6 від 7.02.2005 р.

Укладачі:професор Куліш Ю. В.,

ст. викладач Рибачук О. В.

Рецензент доцент Р.О. Єфременко

Вступ

Дані методичні розробки разом з робочим зошитом складені для виконання студентами загально-технічних спеціальностей завдань з теми диференціальні рівняння. Ці методичні вказівки основані на МВ: Куліш Ю.В., Рибачук О.В.  ’’Диференціальні рівняння’’ УкрДАЗТ. Харків. 2002. 54 ст. (№1005). Далі ми будемо посилатися на ці МВ наступним чином: ДР-1005. В даних МВ ми зберігаємо нумерацію розділів, формул і прикладів з ДР-1005.

Диференціальним називається рівняння, яке містить незалежні змінні, невідому функцію і її похідні. Диференційне рівняння (ДР) для функції однієї змінної називається звичайним ДР, а для функції багатьох змінних – ДР в частинних похідних. Порядком ДР називається порядок старшої похідної в ньому.

1 Диференціальні рівняння першого порядку

1.1 Рівняння з відокремлюваними змінними

Ці рівняння можна представити у вигляді

Тобто похідна може бути представлена у вигляді добутку функції тільки ( ) на функцію тільки . При цьому .

2. Однорідне рівняння першого порядку

В цьому рівнянні похідна може бути представлена у вигляді функції відношення , тобто

Для розв’язання (1.4) вводимо нову змінну і

Останнє рівняння представляє собою рівняння з відокремлюваними змінними .

1.3 Лінійні рівняння

Рівняння першого порядку:

називають лінійним. Функції називаються коефіцієнтами. Якщо то лінійне рівняння називається однорідним або ДР без правої частини. Якщо то лінійне рівняння називається неоднорідним або ДР з правою частиною.

1.5.1 Приклади розв’язання завдань

Приклад 1.5.1 (до завдання №1)

(1.16)

Це рівняння з відокремлюваними змінними (1.2), де , . Ми одержуємо послідовно:

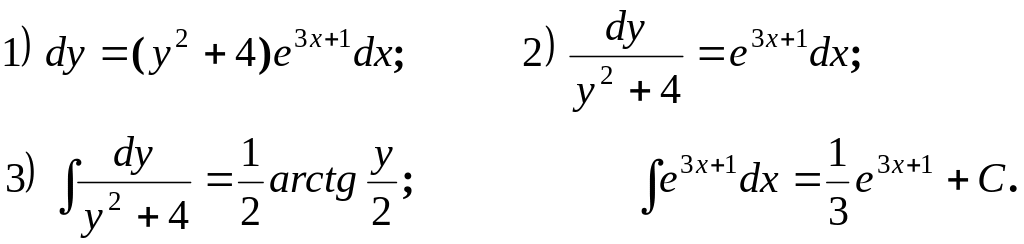
Результат розв’язання ДР можна записати у вигляді загального інтеграла і загального розв’язку:

. (1.17)

Приклад 1.5.2 (до завдання №1)

Це однорідне рівняння першого порядку. При цьому . Вводимо .

Тоді рівняння (1.20) прийме вигляд або .

Отримали ДР з відокремлюваними змінними.

Далі одержуємо Знайдемо загальний інтеграл:

.

Для обчислення вводимо нову змінну . Тому загальний інтеграл має вигляд:

.

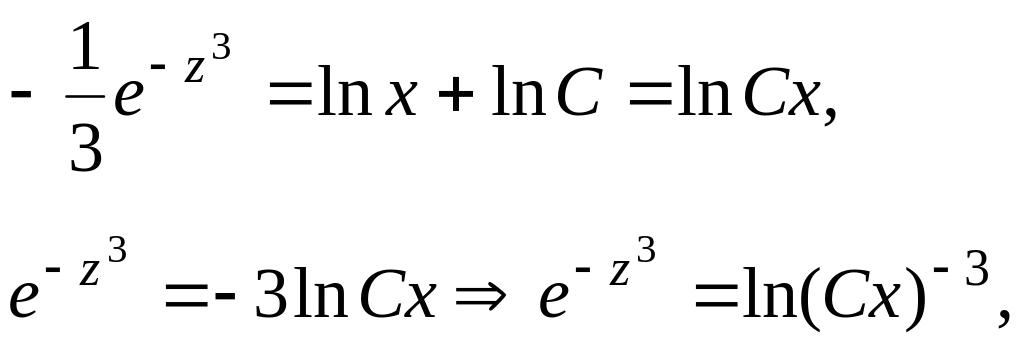
Загальний розв’язок має вигляд

. (1.19)

Приклад 1.5.3 (до завдання №2)

(1.20)

Це лінійне неоднорідне рівняння (1.7) з , .

Нехай Для u маємо ДР з відокремлюваними змінними

Знайдемо його розв’язок :

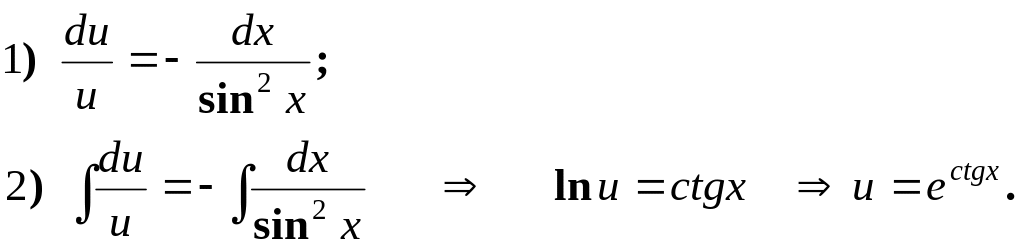
Для v(x) одержуємо

Загальний розв’язок ДР (1.18) має вигляд

. (1.21)

При цьому

2 Диференціальні рівняння другого порядку

2.1 Рівняння другого порядку які допускають зниження порядку

Найбільш просто знижується порядок і навіть інтегрується ДР вигляду . Для інтегрування цього ДР достатньо двічі проінтегрувати ліву і праву частини цього рівняння.

Розглянемо інші ДР які допускають зниження порядку.

1. Рівняння виду . Ці рівняння не містять невідомої функції . До таких рівнянь відносяться ДР

. (2.2)

Для їхнього інтегрування позначимо . Тоді і ми одержуємо ДР першого порядку для функції :

. (2.3)

Якщо позначити розв’язок цього рівняння , то можна одержати загальний розв’язок

. (2.4)

2. Рівняння виду . В таких рівняннях немає явно незалежної змінної . Прикладом таких ДР є рівняння

. (2.5)

Для інтегрування цього ДР вводимо заміну . Тоді

і ми одержуємо ДР

. (2.6)

Це ДР першого порядку для функції , яку розглядаємо як функцію від - невідомої функції ДР (2.5). Якщо знайдено загальний розв’язок (2.6)

, (2.7)

то можна написати загальний інтеграл ДР (2.5)

. (2.8)

Приклад 2.1.1 (до завдання №3)

(2.9)

Це рівняння не містить явно у. Як і в (2.2) вводимо Тоді

Це лінійне рівняння першого порядку для функції р(х). Нехай тоді

.

Для v(x) маємо

,

,

і

.

Знайдемо з допомогою інтегрування частинами:

=

.

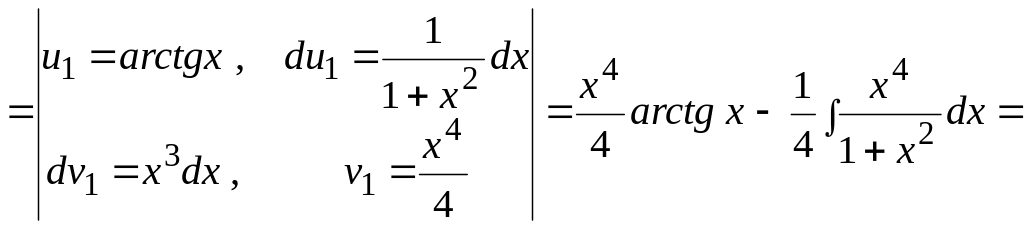
Тому

(2.10)