Екстремуми функції двох змінних

Точка називається точкою екстремуму функції двох змінних , а саме точкою максимуму або точкою мінімуму, якщо функція визначена в околі точки , та її значення в цій точці є відповідно найбільше або найменше значення функції в цьому околі. Значення функції в точках екстремуму називаються екстремальними.

Розглянемо необхідні і достатні умови існування екстремуму.

ТЕОРЕМА. Необхідна ознака екстремуму.

Якщо в точці функція , що диференціюється, має екстремум, то точка є стаціонарною.

Точка , в якій частинні похідні дорівнюють нулю: , або хоча б одна з них не існує називається стаціонарною точкою функції .

Проте умови (вони називаються умовами стаціонарності функції) не є достатніми, тобто їх виконання не гарантує існування екстремуму в точці .

ТЕОРЕМА. Достатня ознака екстремуму.

Нехай функція має в точці неперервні частинні похідні другого порядку (двічі неперервно дифференційовна) і точка – її стаціонарна точка. Позначимо через визначник

.

Тоді:

a) Якщо , то в точці є екстремум, причому

у випадку (або ) – мінімум

а у випадку (або ) – максимум.

б) Якщо , то в точці екстремуму немає (такі точки називаються сідловими).

в) Якщо , то для відповіді на питання про існування екстремуму потрібне додаткове дослідження з використанням диференціалів третього або більш високого порядку (невизначений випадок).

Приклад 11. Знайти екстремуми функції

.

Знайдемо стаціонарні точки:

Таким чином, функція має дві стаціонарні точки і . Обчислюємо значення визначника й :

Звідки , значить, в точці є екстремум, а оскільки , то цей екстремум – максимум і його значення .

, значить, в точці екстремуму немає. Це – сідлова точка.

Визначення емпіричної залежності методом найменших квадратів

Експерементальні дані часто використовують для встановлення функціональної залежності одних величин від інших. Наприклад, при різних температурах виміряна довжина металевого стержня , тобто отримана таблично задана функція . Виникає задача визначення за експерементальними даними аналітичної формули для цієї функції. Такі формули називаються емпіричними.

П

Мал.. 5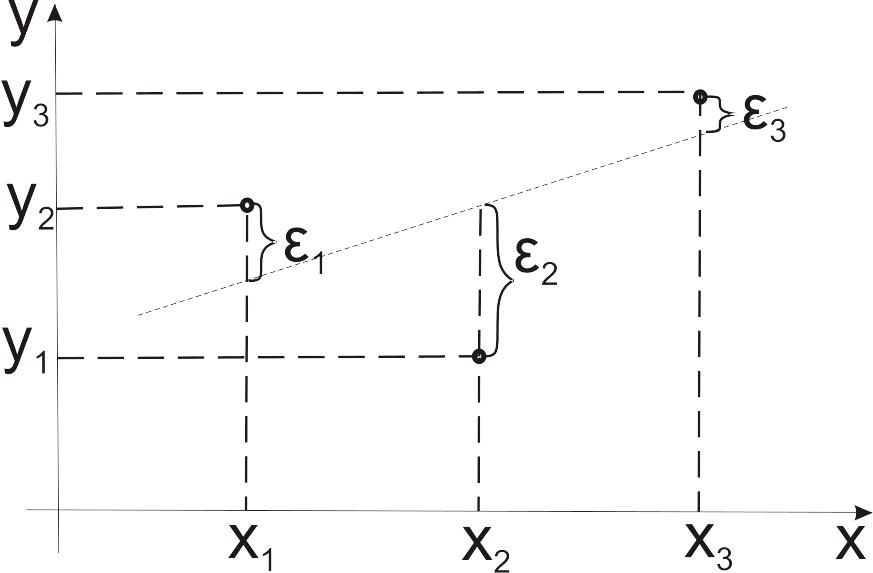

ри розв'язанні цієї задачі, перш за все, з аналізу експерементальних даних або інших міркувань встановлюється вид шуканої залежності. Наприклад, передбачається наявність лінійної залежності . Можуть розглядатися і складніші функції: квадратична , дробово-раціональна та інші. Тут ми розглянемо найпростіший випадок визначення лінійної залежності . Задача звелася до визначення відповідних коефіцієнтів а і b.

Представимо експерементальні дані на графіку (мал.5), на якому зобразимо також шукану функцію (її графік – пряма). Позначимо через нев'язки або похибки формули, тобто різниці експерементальних даних і теоретичних значень цієї величини: . Поява нев'язки практично неминуча, оскільки, навіть якщо між величинами у і x є точна лінійна залежність, наврядчи вдасться провести пряму через усі експерементальні точки внаслідок існування помилок вимірювань.

Природно вважати найкращою таку залежність, для якої невязки в сукупності будуть (в деякому розумінні) найменшими. Суть методу найменших квадратів полягає в тому, що параметри а і b підбираються так, щоб була мінімальною сума квадратів всіх невязок. Таким чином, задача зводиться до визначення точки мінімуму функції

(14)

Знайдемо стаціонарні точки з умови .

.

Позначаючи

,	(15)
приходимо до системи ,		(16)

з

мал.6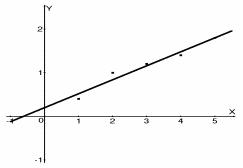

відки, знаходимо . Перевіряючи достатні умови існування екстремуму, можна переконатися, що знайдена стаціонарна точка (а;b) і є шукана точка мінімуму (це витікає, втім, із змісту задачі).

	1	2	3	4	5
	0,4	1,0	1,2	1,4	1,8

Приклад 12. Знайти за допомогою методу найменших квадратів рівняння лінійної залежності за експерементальними даними, зведеними в таблицю

Розв'язок. За формулами (15) знаходимо F=5, оскільки в таблиці наведено 5 пар ( , ), G=1+2+3+4+5=15, H= =55, A=0,4+1,0+1,2+1,4+1,8=5,8, B= =20,6. Далі, розв‘язуючи систему (16) , знаходимо . Таким чином, шукана залежність має вигляд . Представимо знайдену лінійну залежність і експерементальні дані на графіку (мал. 6). Бачимо, що знайдена залежність достатньо добре апроксимує дані.