
- •1. Необходимые и избыточные измерения. Невязки.
- •3. Математическая постановка задачи совместного уравнивания нескольких измеренных величин.
- •4.Вычисление весовых коэффициентов по способу Ганзена.
- •5. Принцип наименьших квадратов.
- •10. Составление условных и нормальных уравнений коррелат в нивелирных сетях
- •11.Нормальные уравнения поправок к выбранным параметрам
- •13. Нахождение неизвестных и поправок в результаты измерений
- •14. Линейные условные уравнения
- •15. Порядок уравнивания параметрическим способом
- •17.Алгоритм Гаусса
- •18. Необходимость решения задачи уравнивания и сущность уравнивания в коррелятном способе.
- •19. Сокращенная схема решения нормальных уравнений
- •20. Лемма Гаусса
- •21 Составить условное уравнение дирекционных углов , если измерены все промежуточные углы, которые близки по величине.
- •22. Промежуточный контроль составления и решения нормальных уравнений
- •24. Выразить поправки в углы четырехугольника проф.Зубрицкого через коррелаты.
- •33. Таблица коэффициентов условных уравнений. Порядок заполнения и вычисления
19. Сокращенная схема решения нормальных уравнений
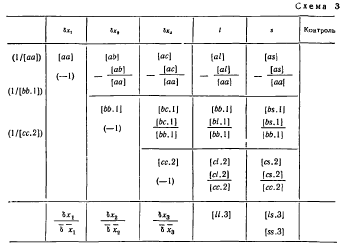
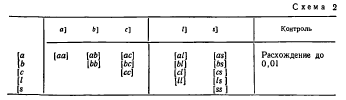
Схема представляет собой сокращенную схему Гаусса, в которой
опущены промежуточные записи, связанные с раскрытием алгоритмов. Все алгоритмы Гаусса в этой схеме получаются методом накопления на счетчиках механических или электрических вычислительных машин. Если выполнить порядковую нумерацию строк в схеме, опустив элиминационные строки, то можно сформулировать следующее правило вычисления коэффициентов этих строк; любой коэффициент, расположенный в i-й строке и j-м столбце схемы, равен соответствующему коэффициенту из схемы 2 плюс сумма произведений уже полученных чисел элиминационных строк из столбца / на числа из столбца j, расположенные над ними (в эквивалентных строках).
Неизвестные
 вычисляются по следующему правилу:
неизвестное
вычисляются по следующему правилу:
неизвестное
 с j
равно числу j-й
элиминационной строки из столбца l
плюс сумма произведений уже вычисленных
неизвестных
на расположенные над ними числа из этой
же элиминационной
с j
равно числу j-й
элиминационной строки из столбца l
плюс сумма произведений уже вычисленных
неизвестных
на расположенные над ними числа из этой
же элиминационной
строки.
20. Лемма Гаусса
Лемма Гаусса имеет вид АТРV = 0.
21 Составить условное уравнение дирекционных углов , если измерены все промежуточные углы, которые близки по величине.
 При
уравнивании полигонометрических сетей
условные уравнения чаще всего составляют
для отдельных ходов, входящих в сеть. В
каждом ходе возникает три условных
уравнения – 2 условных уравнения
координат и 1 -уравнение дирекционных
углов, которое имеет вид
При
уравнивании полигонометрических сетей
условные уравнения чаще всего составляют
для отдельных ходов, входящих в сеть. В
каждом ходе возникает три условных
уравнения – 2 условных уравнения
координат и 1 -уравнение дирекционных
углов, которое имеет вид

Где
 - поправки приближенных значений узловых
- поправки приближенных значений узловых
направлений, а невязка

Если
 безошибочны, то поправки
равны
нулю
безошибочны, то поправки
равны
нулю
22. Промежуточный контроль составления и решения нормальных уравнений
В таблице коэффициентов условных уравнений подсчитывают [a], [b], [f], [S] - cуммы чисел по столбцам.
Д ля контроля последующих вычислений по строкам таблицы находят суммы коэффициентов Si = ai + bi + fi , (i = 1, 2, …, n).
[S] = [a] + [b] + [f] - контроль вычисления Si.
При
решении нормальных уравнений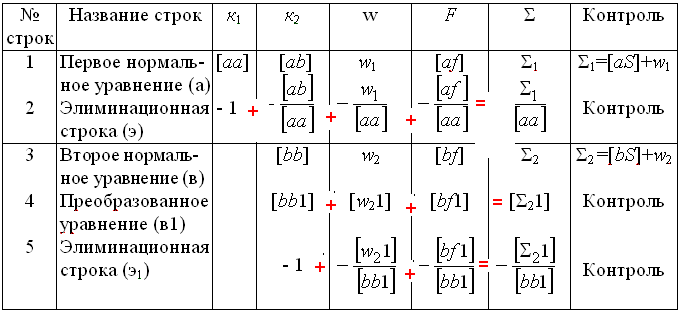 сумма
по элиминационной строке или преобразованной
без ячейки столбца ∑ должна равнятся
полученной в ячейке ∑
сумма
по элиминационной строке или преобразованной
без ячейки столбца ∑ должна равнятся
полученной в ячейке ∑
Заключительный контроль решения нормальных уравнений осуществляется подстановкой коррелат в суммарное уравнение:
([aS] - [af])к1 + ([bS] - [bf])к2 + ... + ([rS] - [rf])кr + [w] = 0
24. Выразить поправки в углы четырехугольника проф.Зубрицкого через коррелаты.
В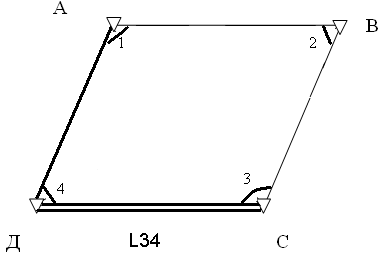 4-угольнике Зубрицкого измеряются все
четыре угла и одна сторона, значит
количество выполненных измерений n=5,
а необходимых измерений t=4-
по количеству измеренных углов
4-угольнике Зубрицкого измеряются все
четыре угла и одна сторона, значит
количество выполненных измерений n=5,
а необходимых измерений t=4-
по количеству измеренных углов
Число независимых условных уравнений r=5-4=1
Невязка в четыге
33. Таблица коэффициентов условных уравнений. Порядок заполнения и вычисления
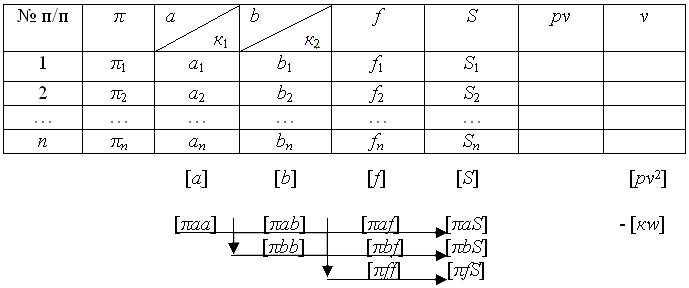
 –
обратный вес результата
измерения
–
обратный вес результата
измерения

Н апример имеем нивелирную сеть Система условных уравнений поправок
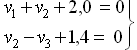
Весовая функции F=HI=f0+ν1
Таблица
коэффициентов условных уравнений
38. Нормальные уравнения коррелат.
Имеют вид
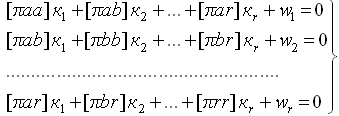
– обратный вес результата измерения
Для нахождения коэффициентов
