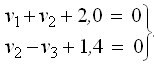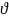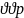10. Составление условных и нормальных уравнений коррелат в нивелирных сетях

Пусть r = 2 и от системы условных уравнений поправок

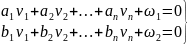
требуется перейти к системе нормальных уравнений коррелат

Подлежит оценке точности весовая функция

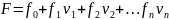
С этой целью коэффициенты условных уравнений и функции записывают по столбцам в таблицу. Под таблицей помещают вычисленные значения коэффициентов нормальных уравнений коррелат, а также величины [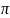 af], [ bf], [ ff], необходимые для дальнейшей оценки точности функции. Столбцы pν и ν заполняют позднее

Таблица коэффициентов условных уравнений и функции

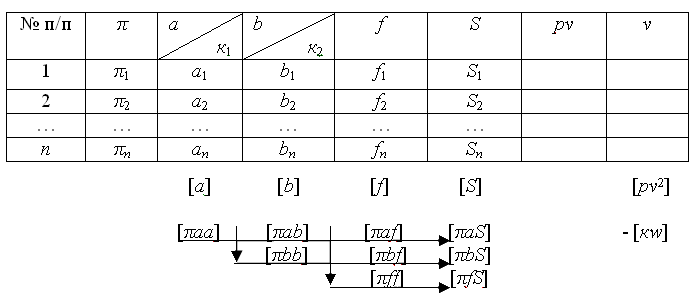
Здесь [a], [b], [f], [S] - cуммы чисел по столбцам.

[πaa] = π₁a₁a₁ + π₂a₂a₂ +...+ π_na_na_n; [πab] = π₁a₁b₁ + π₂a₂b₂ +...+ π_na_nb_n и т.д.

Для контроля последующих вычислений по строкам таблицы находят суммы коэффициентов

S_i = a_i + b_i + f_i , (i = 1, 2, ..., n).

[S] = [a] + [b] + [f] - контроль вычисления S_i.

Контроль вычисления коэффициентов нормальных уравнений

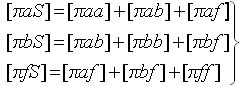
11.Нормальные уравнения поправок к выбранным параметрам

Нормальные уравнения в параметрическом способе имеют вид

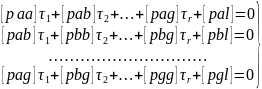
Где 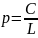– вес, 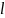– свободные члены. Из решения этой системы получают поправки к приближенным значениям неизвестных.

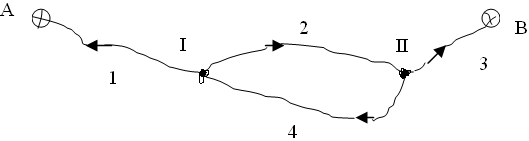
Для составления нормальных уравнений поправок (НУП) сначала выбирают параметр – например высоту неизвестного пункта Н_I, H_II, потом находят их приближенные значения 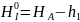, 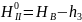По этим значениям находим свободные члены

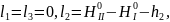
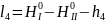
Потом составляем таблицу для нахождения коэффициентов нормальных уравнений 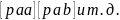(табл. 1 лабор), по полученным внизу таблицы коэффициентам составляют НУП, которые например примут вид

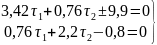
13. Нахождение неизвестных и поправок в результаты измерений

При уравнивании параметрическим способом при решении системы нормальных уравнений поправок (СНУП) получают поправки , прибавив их к приближенным значениям неизвестных получают искомую неизвестную

Например в нивелирном ходу 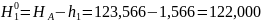м

После решения СНУП

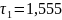
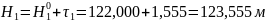
Искомые значения можно получить и вторым способом – найти поправки в превышения ходов, получить уравненные превышения и по ним найти неизвестную высоту

Поправку вычисляют по формуле

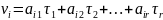
№№ хода	Вес, p	a1	a2	Свободные члены l	∑
1	2	-1		0	-1	-1.555
2	1	-1

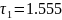
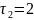
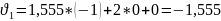
14. Линейные условные уравнения

имеют вид

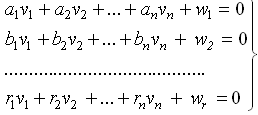
Например в нивелирной сети

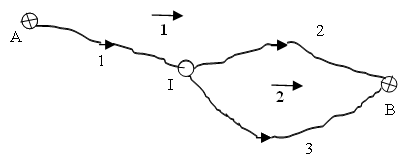
условные уравнения связи

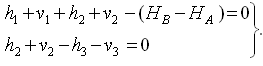
Для перехода к условным уравнениям поправок достаточно вычислить невязки.

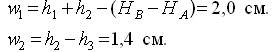
Условные линейные уравнения поправок имеют вид: