1. Необходимые и избыточные измерения. Невязки.

Необходимые измерения( k)- измерения, которых было бы достаточно для определения искомых величин.

На практике число выполненных измерений п всегда больше числа необходимых измерений.

Избыточные измерения (r) – это разность между выполненными измерениями и необходимыми r = п — k

В полигонометрическом ходе выполнено п_S измерений длин сторон и п_β = п_S + 1 измерений углов. n=п_S + п_β= п_S+ п_S+1= 2п_S+1. Число необходимых измерений равно удвоенному числу определяемых пунктов, так как для каждого пункта необходимо получить 2 координаты: х и у, т . е. k= 2(п_S — 1)

r=2п_S+1-2(п_S — 1)=3

В сети триангуляции пункты А, В, С, О, Е исходные. Для определения координат 3 пунктов (1, 2, 3) измерен 21 угол. Получаем r = 21 — 2*3=15. В нивелирной сети r = 5 — 2 = 3.

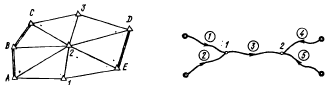
Невязка – разность между значением функции, вычисленным по результатам измерений, и истинным ее значением, возникающая вследствие неизбежных погрешностей измерений.

Разновидности невязок:

- фактическая и допустимая (найденная по формуле) - cравнивая их определяют качество выполненных работ.

- относительная и абсолютная - характеризуют качества работы

- угловая, линейная, высотная - невязки характеризующие погрешность определенного вида измерений.

Наличие избыточных измерений позволяет определить величину невязки, а значит повысить точность искомых величин, выполнить оценку точности самих измерений и надежно их проконтролировать.

3. Математическая постановка задачи совместного уравнивания нескольких измеренных величин.

Главная задача, которая должна быть решена при уравнивании. — устранение всех невязок, для чего, необходимо исправить результаты измерении. Другая задача — оценка точности по материалам уравнивания.

Пусть для решения некоторой задачи измерено п величии, истинные значения которых обозначим через X₁…Х_n. Результаты измерений х₁ …х_п этих величии получены соответственно с весами р₁… р_п. По условию задачи известно, что измеренные величины связаны между собой уравнениями

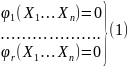
Система состоит только из независимых между собой уравнений, называемых условными, число которых = числу избыточно измеренных величии r, которое всегда меньше п, поэтому система содержит уравнений меньше, чем неизвестных и допускает бесконечное множество решений.

Система с измеренными величинами имеет вид:

Так как измерения содержат ошибки, то в правых частях не 0, а величина невязки W. При уравнивании сначала проверяют допустимость невязок и отбраковывают измерении, не в допуске и с грубыми ошибками.

Обозначая исправленные результаты измерений через 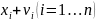, где 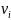— искомые поправки, получаем

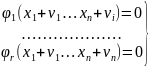
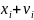называют уравненными значениями измеренных величин. Эта система, как и (1) неопределенная и допускает бесконечное множество решений.

Цель уравнивания — найти такие поправки к измеренным значениям 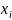, которые позволили бы ликвидировать невязки W_i. При выборе пути решения задачи уравнивания надо стремиться, чтобы поправки были близки по абсолютной величине ошибкам измерений с противоположным знаком. Тогда, значения искомой величины, полученные разными путями будут равны (уравнены)