1.Закон сохранения электрического заряда. Закон Кулона.
Электрический
заряд- это физическая величина являющая
количественной мерой способности
большинства элементарных частиц
образующих тело оказывать особое
(электрическое) воздействие друг на
друга. Электрические заряды бывают
полож и отриц. З-н
сохранения зарядов:
в электрически изолированной системе
полный заряд т.е. алгебраическая сумма
полож и отриц зарядов с течением времени
не изменяется при любых процессах
происходящих в этой системе. Математически
этот закон записывается
,
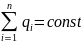Заряд квантуется q=Ne.
Заряд является реалитивистки-инвариантный,
т.е. не зависит от того движется он или
покоится.
Количественно взаимодействие оценивается по закону Кулона
2.Электрическое поле и его основные характеристики-напряженность, потенциал. Принцип суперпозиции электрических цепей.
Всякий электрический заряд изменяет определенным образом свойства окружающего его пространства, т.е. создает электрическое поле. Это поле проявляет себя в том, сто помещенный в какую-либо точку другой, «пробный» заряд, заряд испытывает действие силы.
Силовой характеристикой электростатического поля является напряженность E=F/qпр. Если положить qпр=1, то численно E=F. Напряженность поля точеного заряда в вакууме
.
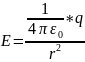Если поле образовано несколькими
зарядами, то согласно принципу
суперпозиции
.
Величина φ=Wр/qпр называется потенциалом поля в данной точке. Потенциал численно равен потенциальной энергии которой обладает в данной точке единичный положительный заряд. Значит, потенциал является электрической характеристикой электростатического поля.
По другому: потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки в бесконечность φ=Ар/q.
Потенциал
поля точечного заряда
.
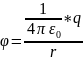И поля системы зарядов
.
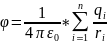В вакууме.
3.Напряженность как градиент потенциала.
Потенциал вектора Е на координатные оси выражается через потенциал следующим образом
,
,
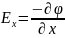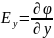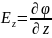тогда
=
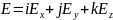Выражение стоящее в скобках называется градиентом скаляра φ и обозначается qrad φ. E=- qrad φ, что представляет собой связь между напряженностью и потенциалом.
Градиент потенциала характеризует быстроту изменения потенциала в направлении силовой линии.
Вектор Е направлен в сторону убывания потенциала, это свидетельствует знак минус.
Для
однородного поля Е и φ связаны.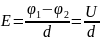
,
где
d-расстояние
между точками 1 и2, φ1-φ2=U-разность
потенциалов между этими точками.
4.Поток вектора напряженности. Теорема для электростатического поля в вакууме.
С помощью вектора напряженности эл.ст./п. определяют направление поля и его величину.
Для определения направления поля вводят понятие линии напряженности или силовые линии- линии касательные к которым в каждой точке совпадают с направлением вектора E. Поток вектора напряженности эл.ст./п. – есть физ. величина равная скалярному произведению
dФ=E
dS
cosα=E
ds;
Ф=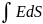
Теорема Гаусса:
Поток
вектора напряженности эл.ст./п. в вакууме
через любую замкнутую поверхность равна
алгебраической сумме зарядов заключенных
внутри данной замкнутой поверхности
деленной на 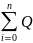ε₀
=
/ε₀