3.Исследование напряженно-деформированного состояния

В предыдущих главах были рассмотрены простые виды деформации: растяжение-сжатие, сдвиг, кручение, изгиб, где в условие прочности входило одно напряжение: либо нормальное σmax, либо касательное τmax. Чтобы перейти к рассмотрению общего случая нагружения тела (к сложному сопротивлению), при котором величины σ и τ в точке тела могут быть одного порядка, надо вначале получить общую форму записи условия прочности, в которой бы учитывалось влияние и σ и τ.

В общей постановке уравнения связи между перемещениями, деформациями, напряжениями и внешними нагрузками рассматриваются в механике деформируемого твердого тела и в теории упругости. В этой главе приводятся только основные сведения, необходимые для решения поставленных задач.

Рассмотрим напряжения и деформации, которые возникают в некоторой точке тела при произвольном нагружении.

3.1. Напряжения

В теле произвольной формы, нагруженном произвольными силами выделим элементарный объем. По граням этого элемента действуют векторы полных напряжений величина и направление, которых неизвестны. Для определения этих векторов представим каждый из них в виде проекций на оси координат xyz.

Пусть объем выделенного элемента стремится к нулю, тогда можно считать, что напряжения на противоположных гранях элемента одинаковы и определяют напряженное состояние в точке тела, около которой выделен этот объем.

Запишем напряжения, действующие по граням элемента, в упорядоченном виде, в виде матрицы размерностью 3х3. Каждый столбец этой матрицы представляет собой совокупность напряжений, действующих на одной из граней элемента. такая матрица называется тензор напряжений.

(3.1)

Следует отметить, что тензор не просто матрица. Компоненты тензора подчиняются строгим правилам преобразования, излагаемым в тензорной алгебре. Механика деформируемого твердого тела. теория упругости. численная механика строятся на таких ключевых понятиях, как тензор напряжений и тензор деформаций. Без них невозможно создание численных методов расчета, таких, как метод конечных элементов и метод граничных элементов. В сопротивлении материалов используются не сами тензоры

23

напряжений и деформаций, а лишь их отдельные компоненты.

При повороте осей координат, совпадающих с нормалями к граням выделенного элемента, компоненты напряжений изменяются. Вращая выделенный элемент вокруг осей координат, можно найти такое положение элемента, при котором все касательные напряжения на гранях элемента равны нулю.

Площадка, на которой касательные напряжения равны нулю, называется главной плошадкой. Нормальное напряжение на главной площадке называется главным напряжением.

Нормаль к главной площадке называется главной осью напряжений. В каждой точке можно провести три взаимно-перпендикулярных главных площадки. Различают три вида

напряженного состояния: линейное, плоское и объёмное.

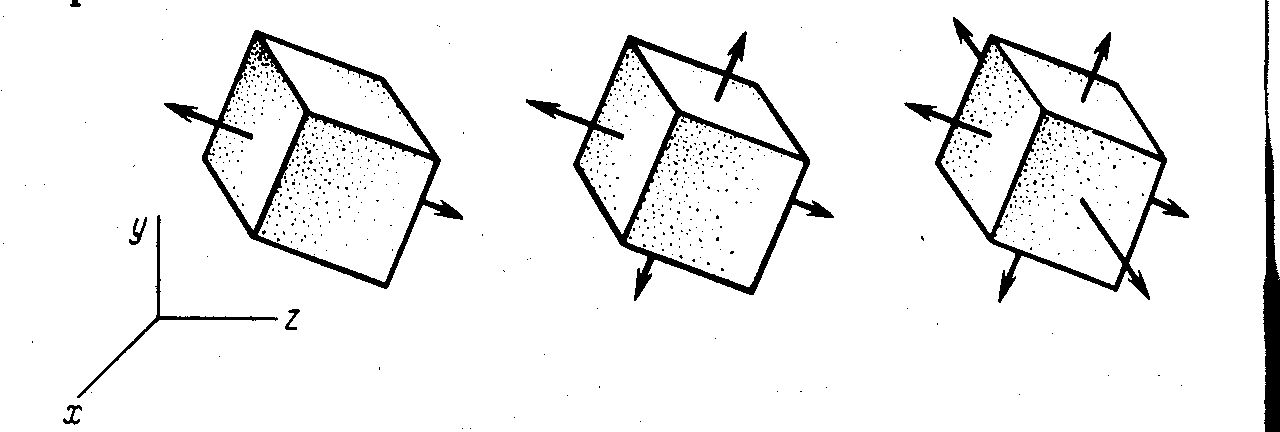
Рис.3.1.Линейное,плоское и объемное напряженное состояние, представленные главными напряжениями

В зависимости от величины каждого из трёх главных напряжений им присваивается индекс от 1 до 3.

σ1 > σ2 > σ3 (3.2)

Линейное напряженное состояние возникает, когда одно главное напряжение не равно нулю.

Плоское напряженное состояние возникает, когда два главных напряжения не равны нулю.

Объёмное напряженное состояние возникает, когда три главных напряжения не равны нулю.

Правило знаков для напряжений:

Для нормальных напряжений растяжение «+», для касательных ,при обходе элементарного объёма против хода часовой стрелки- «+».

3.2. Линейное напряженное состояние (одноосное)

Присуще растяжению или сжатию прямых стержней.

Рис.3.2.Напряженное состояние в растянутом стержне по сечению mn

Полное напряжение в сечении mn

(3.3)

24

нормальное напряжение, действующее по наклонной площадке.

Касательное напряжение (3.4)

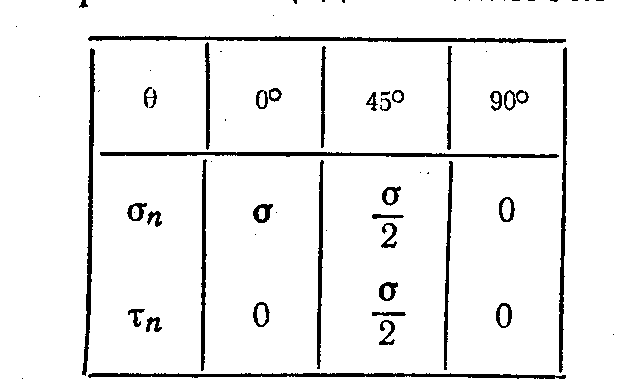
σ_max= σ_n при =0 (3.5)

max= n при =45° (3.6)

s₁₌ σ_max ; σ₂= σ₃=0. (3.7)