2.2. Влияние собственного веса на напряжения и деформации стержней
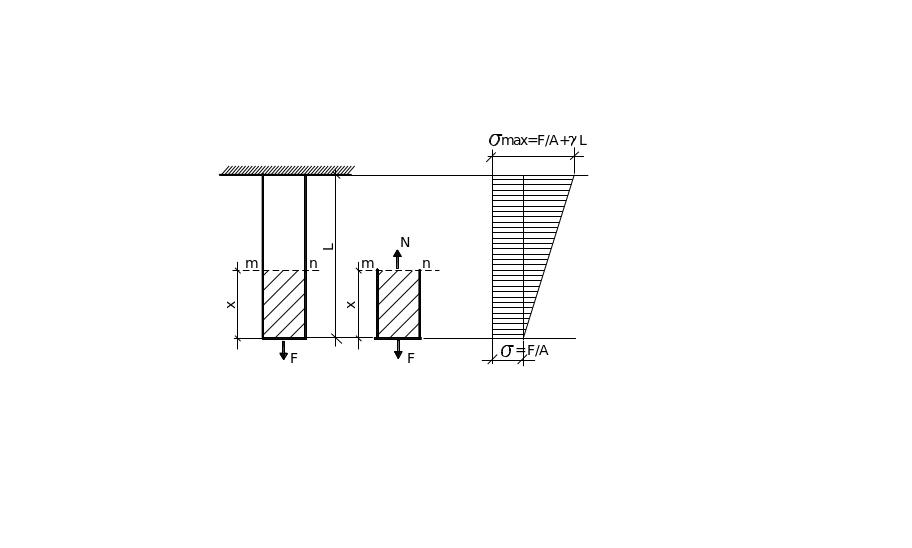
Рис.2.4. Влияние собственного веса
По рис.2.4 в сечении mn , на расстоянии х от нижнего конца, из условия равновесия
N= F+ Qx = F+ x A (2.12)
где -объёмный вес материала стержня.
14
Напряжение в
сечении mn
σ=
+
x
Условие прочности
σmax=
+ L
O
[σ]
(2.13)
Деформация стержня Δ dx = σ dx/ E = N dx/(AE)+ x dx/E
ΔL= Δ dx=N L/(AE) + L2/(2E) (2.14)
Можно показать, что при длине стержней порядка нескольких метров влияние собственного веса составляет 1-3%. Поэтому в таких случаях влиянием собственного веса можно пренебречь.
2.3. Статически определимые стержневые конструкции
Расчет заключается в определении усилий в стержнях, определении деформаций, вычислении напряжений
и в определении перемещений. Признаком таких конструкций является разрешимость с помощью уравнений статики.
Пример.
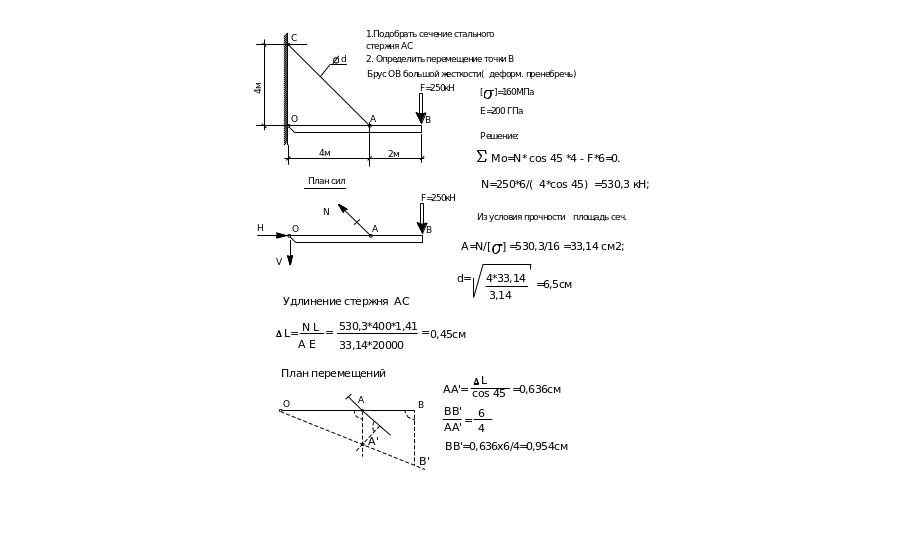
Пример. 1.Определить усилия в стержнях.
2.Определить напряжения и проверить прочность стержней.
3.Вычислить деформации стержней.
4.Определить перемещения точки С.
15
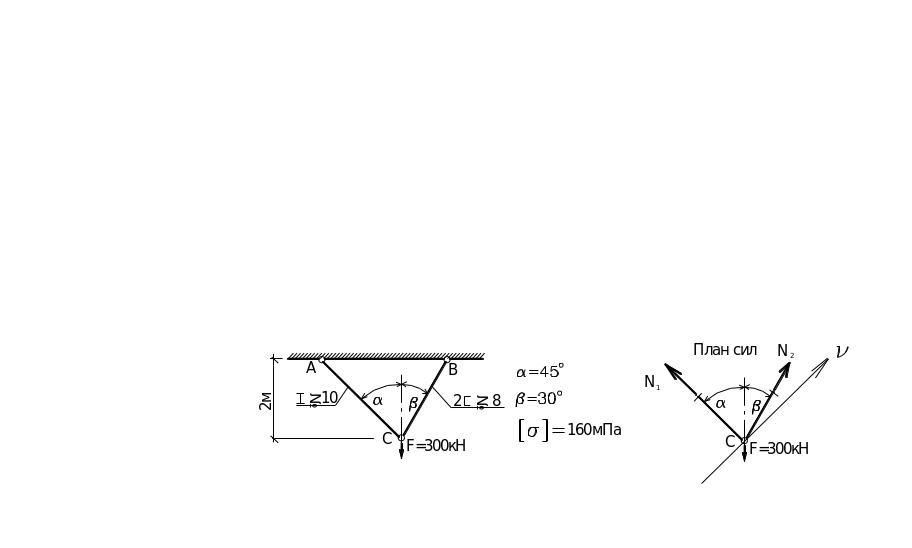
Sn=0; N2` cos 15° - F` cos 45°=0; N2=300` cos 45°/ cos 15°=219,62 кН;
SZ=0; N1` cos 45° + N2` cos 30° -300 =0; N1 = (300 - 219,62 ` cos 30°)/ cos 45°=155,29 кН ;
Оба стержня растянуты
По сортаменту ГОСТ для прокатной стали А1 = 12 см2 ; А2 = 17,96 см2 ;
Проверка прочности
s1 = N1 / А1 =155,29 /12=12,94 кН/см2 <16 кН/см2;
s2 = N2 / А2 =210,62 /17,96=112,23 кН/см2 <16 кН/см2;
Удлинение стержней
DL1= N1` L1 /(А1` E)= 155,29` 200 •1,41/ (2000•12)=0,182 см;
DL2= N2` L2 /(А2` E)= 219,62` 200 /sin 30°/ (2000•17,96)=0,141 см;
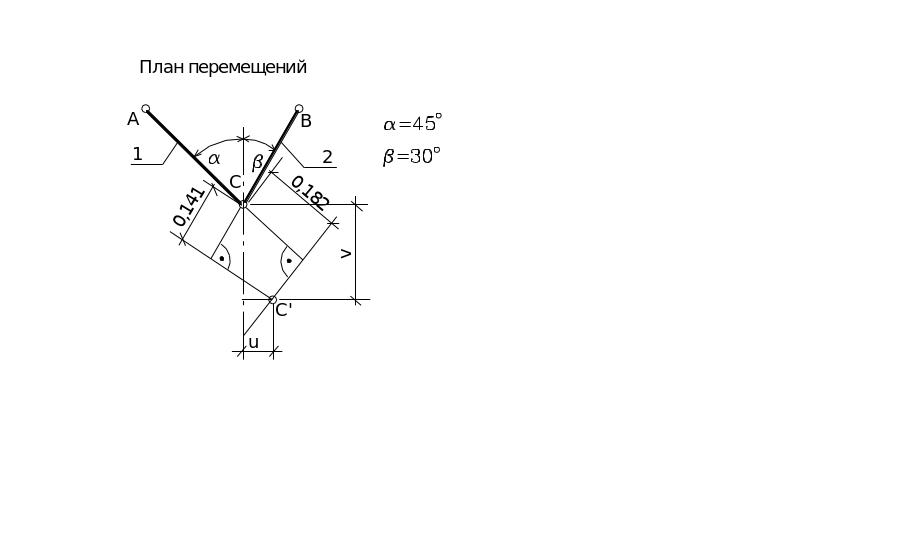
v= DL1/cos 45°-u tg 45°
v = DL2/cos 30°+ u tg 30°
Решая систему из двух уравнений, получим: u=0.06 cм, v=0.197 cм .
2.4. Статически неопределимые стержневые конструкции
Для присоединения очередного узла в стержневых неизменяемых системах требуется, как минимум, два стержня. В таких случаях говорят о минимуме необходимых стержней для обеспечения геометрической
неизменяемости. Образованные т.о. системы могут быть разрешены с помощью одних уравнений статики, а сами конструкции относят к статически определимым.
Если число стержней превосходит необходимый минимум, тогда говорят о «лишних» связях, саму систему
квалифицируют как «статически неопределимую». Для разрешения такой системы требуется составлять дополнительные уравнения. При наличии лишних стержней перемещения не могут быть произвольными и должны быть связаны определенными зависимостями. Деформации стержней не должны разъединять узловые соединения, т. е. необходимо обеспечить совместную деформацию.
Для всякой пространственной системы сил можно составить систему из 6-и уравнений равновесия и, решив ее, найти 6 неизвестных сил. Однако среди этих уравнений могут быть тождества, обращающиеся в нуль при любых значениях нагрузок. Это бесполезные уравнения и, следовательно, число неизвестных сил
должно быть равно числу уравнений минус число тождеств.
Для произвольной плоской системы сил можно составить 3 уравнения, не являющихся тождествами, например, сумму проекций всех сил на 2 любые оси и одну сумму моментов всех сил, относительно какой-либо точки.
16
Для плоской системы сходящихся сил можно составить лишь 2 уравнения, не являющихся тождествами. Сумма моментов всех сил относительно точки их пересечения тождественно равна нулю. Из 2-х уравнений (любых) можно определить лишь 2 неизвестные силы.
Для плоской системы параллельных сил бесполезной оказывается сумма проекций на ось, перпендикулярную силам. Соответственно из 2-х любых уравнений равновесия можно найти лишь 2 неизвестные силы.
Для системы коллинеарных сил (действующих вдоль одной прямой линии) можно составить лишь одно полезное уравнение „ сумму проекций всех сил на эту прямую, которая равна просто сумме сил.
Система называется статически неопределимой, если число неизвестных в ней больше числа полезных уравнений равновесия.
Степень статической неопределимости равна разности между числом неизвестных и числом полезных уравнений равновесия.
Для раскрытия статической неопределимости существуют разные способы, которые будут рассмотрены далее. Заметим лишь, что всякая реакция возникает в местах наложения внешних связей (ограничений движения системы). Нет ограничения- нет реакции. Есть ограничение - есть реакция. В то же время любая наложенная связь (любое ограничение движения) позволяет составить дополнительное уравнение, называемое уравнением совместности перемещений. В результате появляется возможность сделать число уравнений равным числу неизвестных и решить систему уравнений.
При большом количестве опор и шарниров определить степень статической неопределимости довольно трудно. Проще это сделать следующим образом: мысленно отбрасываем связи по одной до тех пор, пока система не превратится в механизм. Верните на место одну связь (любую). Система станет статически определимой. В таком виде число отброшенных связей равно степени статической неопределимости системы.
Решение статически-неопределимых задач значительно более сложная и трудоемкая задача.
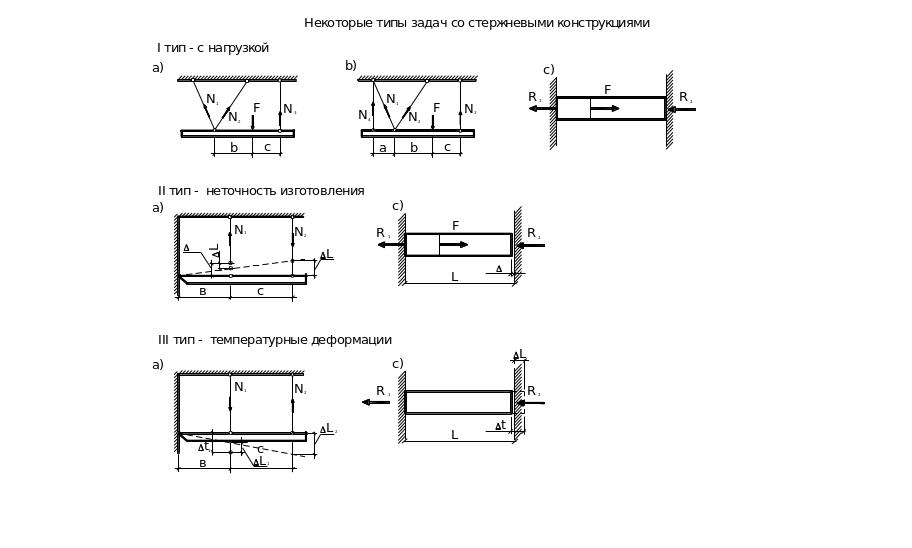
Рис.2.5. Примеры расчётных схем стержневых конструкций
Алгоритм решения статически неопределимых задач
а)определить количество лишних неизвестных;
б)составить необходимое количество дополнительных уравнений, устанавливающих связь с деформациями;
в)выразить деформации через неизвестные усилия и решить их в системе с уравнениями равновесия статики.
17