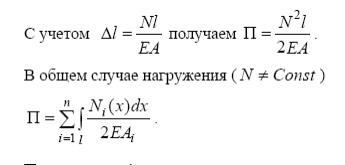1.4 Напряжения

Напряжением называется интенсивность действия внутренних сил в точке тела или, внутреннее усилие, приходящееся на единицу площади. Рассечем тело произвольным сечением (рис. 1.5). Выделим малую площадку dA. Внутреннее усилие, действующее на нее, обозначим dR. Полнoе среднее напряжение, на этой площадке p=dF/dA. Найдем предел этого отношения при dA0 . Это и будет напряжение в точке тела

(1.11)

Рис. 1.5.Определение напряжений в точке

Чтобы задать вектор полного напряжения в точке надо задать его модуль и направление в пространстве, или задать его проекции на оси координат. Спроектируем вектор dR на оси x, y и z, из которых ось х направлена вдоль нормали к сечению, а оси y и z лежат в плоскости сечения. Найдем проекции полного напряжения на оси x, y, и z.

8

– нормальное напряжение;

– касательное напряжение вдоль оси у; (1.12)

– касательное напряжение вдоль оси у;

Полные продольное усилие и поперечные силы для всего поперечного сечения есть интеграл от приведенных выражений по площади сечения А.

1.5. Простейшие типы деформаций на примере стержней

Большинство инженерных конструкций имеют форму, при которой размеры поперечного сечения меньше длины. Для стержней можно привести несколько типов деформаций.

Следует различать деформации и перемещения.

Перемещение - изменение положения точки в пространстве.

Деформация -изменение формы и размеров тела

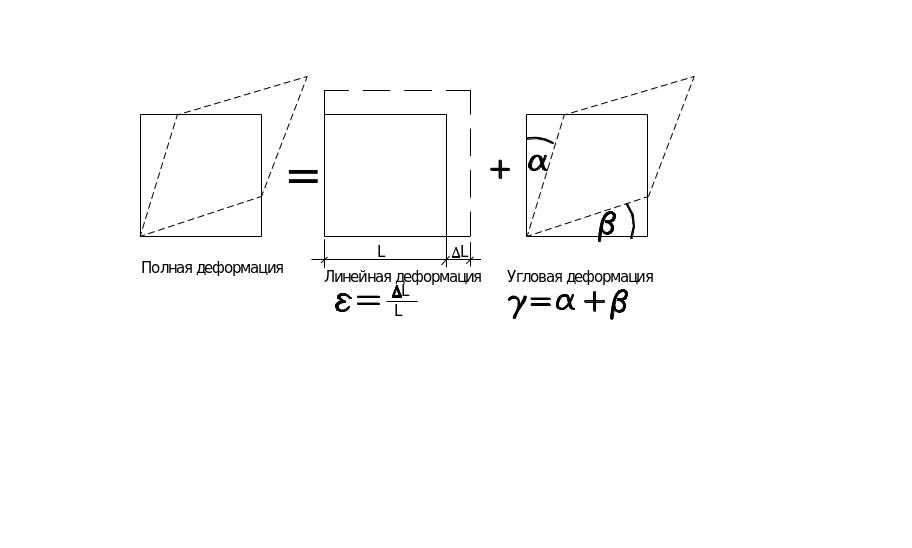
В отдельных случаях их величины могут совпадать, например, при растяжении стержня, но в общем случае это разные вещи. Деформации могут быть угловые и линейные (рис. 1.6).

; ;

Рис.1.6.Схема линейной и угловой деформаций

Линейная деформация характеризует изменение размеров тела. Она бывает абсолютная ΔL и относительная ε=ΔL/L. Использование относительной деформации предпочтительно, так как она не зависит от размеров тела. Угловая деформация характеризует изменение формы тела и чаще всего называется углом сдвига.

9

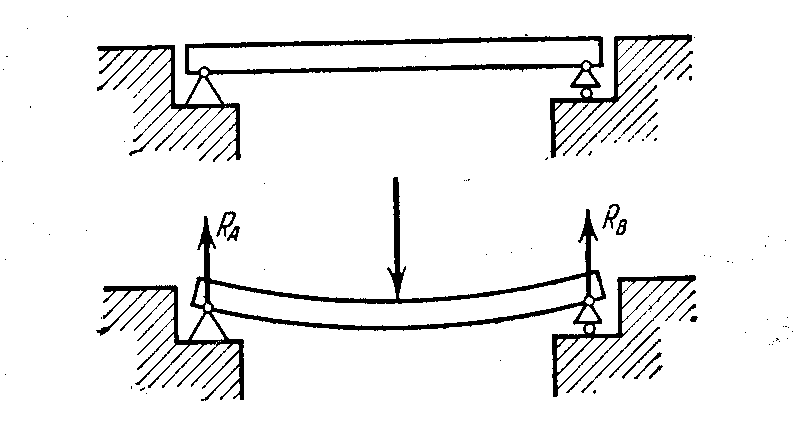
Растяжение-сжатие Изгиб

Сдвиг-смятие Кручение

Рис.1.7. Простейшие типы деформаций

10

2.Осевое растяжение-сжатие призматических стержней

2.1 Внутренние усилия и напряжения в растянутых и сжатых стержнях. Условие прочности.

При растяжении-сжатии все силы направлены вдоль оси стержня. В поперечных сечениях стержня действует только одно внутреннее усилие: продольное. Возможно действие сосредоточенных и распределенных нагрузок.

Правило знаков

Продольное усилие равняется сумме сил, расположенных по одну сторону от рассматриваемого сечения. Положительным считается растягивающее усилие, отрицательным - сжимающее.

При растяжении и при сжатии в поперечных сечениях стержней действует только продольное усилие. Расчетные формулы для растянутых и сжатых стержней одинаковы. Различаются только знаком продольного усилия.

Математически это правило можно записать следующим образом:

(2.1)

Рассмотрим стержень, нагруженный силой F (рис.2.1). Внутренние усилия в поперечных сечениях стержня определяются методом сечений. Из уравнений равновесия отсеченной части стержня продольное усилие N=F, поперечная сила Q=0. , изгибающий момент M=.0;

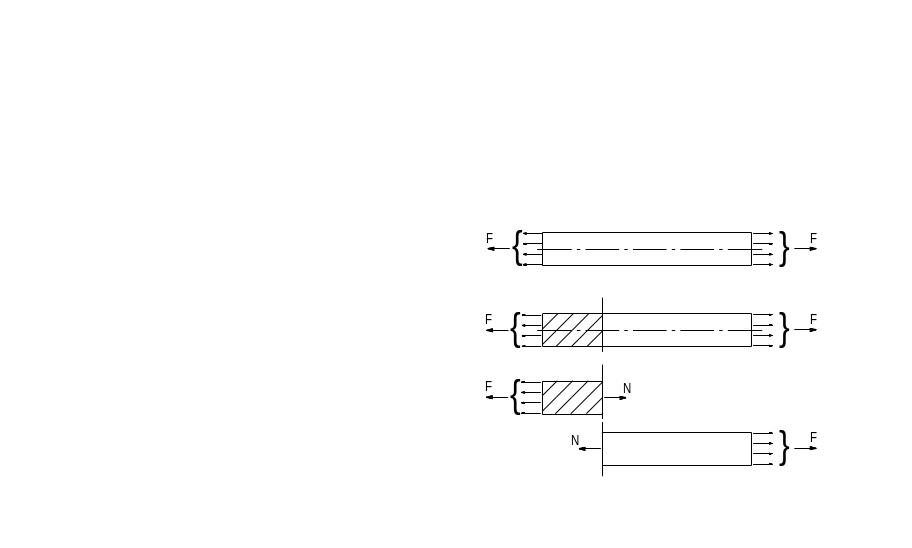
Рис.2.1.Распределение внутренних усилий по сечению

Укажем на стержне произвольное поперечное сечение 1-1. Продольное усилие N для рассматриваемого стержня не зависит от выбранного сечения и эпюра продольных усилий (график распределения продольного усилия по длине стержня) представляет собой прямоугольник. с ординатой F.

Так как напряжение - это внутреннее усилие N, приходящееся на единицу площади, формула для нормальных напряжений σ при растяжении

(2.2)

Поперечная сила при растяжении Q=0, следовательно, вызываемые ею касательные напряжения . τ =0

При растяжении σ >0, при сжатии σ <0.

Условие прочности при растяжении-сжатии

(23)

11

Выражения для max σ взято по модулю, так как допускаемое напряжение всегда положительное.

2.2.Деформации стержней

На рисунке 2.2 показан стержень до и после растяжения. Его длина увеличилась, а поперечный размер уменьшился. Введем понятия абсолютной и относительной деформации.

Под действием силы F стержень удлинился на величину Δl(абсолютное удлинение) , но в силу гипотезы плоских сечений осталось плоским и параллельным своему исходному положению. Перемещения всех точек поперечного сечения одинаковы, деформации и напряжения (в силу закона Гука) также одинаковы. Испытания показывают, что « в упругих телах усилия пропорциональны деформациям». В последствии закон Гука был уточнен, т.к. тела ведут себя подобно упругой модели только в определённом диапазоне.

Современная трактовка закона Гука: « Малые упругие относительные деформации при растяжении и сжатии, не зависящие от времени деформирования, пропорциональны напряжениям».

σ= Е  (2.4)

Е- коэффициент пропорциональности, называемый модулем упругости и имеющий размерность напряжения (давления). Иногда его можно встретить под названием - модуль Юнга.

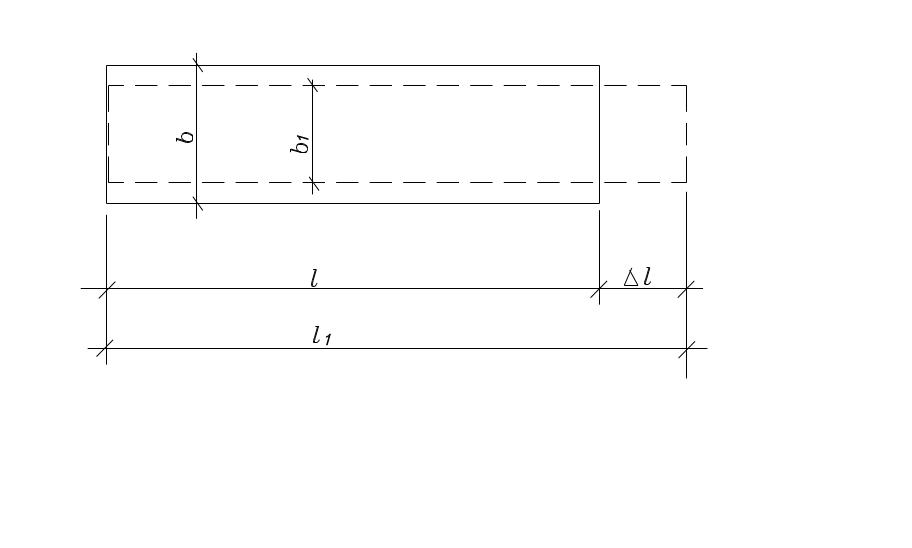
Рис.2.2. Схема удлинения стержня при растяжении

Экспериментально установлено, что при растяжении происходит увеличение длины стержня и уменьшение поперечных размеров см. рис 2.2..

Удлинение Δl= l1-l

l-первоначальная длина;

l1-длина стержня в деформированном состоянии.

Относительное удлинение

e= Δl/l

Аналогично для поперечных размеров

Сужение Δb=b1-b

Относительное сужение

e`= Δb/b; e’=−n⋅ε,

Относительные поперечная и продольная деформации связаны между собой эмпирической зависимостью

где n коэффициент Пуассона, определяемый опытным путем. Знак минус показывает, что при растяжении стержня его поперечное сечение сужается.

12

Коэффициент Пуассона является упругой константой материала. В дальнейшем будет показано, что при упругой деформации 0<n<.0,5. Значения коэффициента для различных материалов приводятся в справочниках. Например,для пробки n≈0; для стали n≈0,3; для резины .n=0,49.

Заменив в формуле (2.4) σ=N/A и  = Δl/l получим формулу для вычисления удлинения стержня

(2.5)

Выражение EA наз. жесткостью стержня при растяжении.

Эта формула справедлива в случае действия одной сосредоточенной силы, то есть продольное усилие постоянно по длине стержня. N

Если на стержень действует несколько сосредоточенных сил, то стержень разбивается на несколько участков (от силы до силы) и полное удлинение равно сумме удлинений каждого участка в отдельности

(2.6)

В общем случае, если продольное усилие на некоторых участках величина переменная, то есть действует распределенная нагрузка, то удлинение пропорционально площади эпюры продольных усилий

(2.7)

Для определения потенциальной энергии воспользуемся, известным из теоретической механики началом возможных перемещений

Начало возможных перемещений

Если тело находится в состоянии равновесия, то сумма работ внешних и внутренних сил равна нулю на любых возможных (согласованных со связями) перемещениях. внешW и внутрW

Заметим, что реальные перемещения- всегда возможные.

Wвнеш+W внутр =.0 (2.8)

При упругой деформации, потенциальная энергия равна работе внутренних сил П

П=W внутр =−Wвнеш. (2.9)

Потенциальная энергия не бывает отрицательной и численно равна площади диаграммы нагружения стержня (при упругой деформации площади треугольника (рис. 4.3)

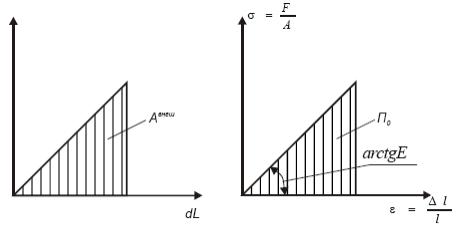
F

Рис.2.3. Диаграммы растяжения в упругой части: dL=f(F) и σ=f()

Поскольку напряжения σ=N/A и деформации ε= ΔL/L есть нагрузка и перемещение, деленные на константы A и L, то и напряжения прямо пропорциональны деформациям. На графике (рис. 2.3) зависимость σ от ε изображается прямой линией. Следовательно, можно записать из (2.5)

σ=Eε, (2.10)

13

где E- коэффициент пропорциональности, называемый модулем продольной упругости или модулем Юнга. Модуль Юнга E- константа материала (как и коэффициент Пуассона n ) приводится в справочниках.

Для стали E=210 ГПа=2.10⁵ МПа=2.10⁴кН/cм²;

Для чугуна E=100 ГПа=1.10⁵ МПа=1.10⁴кН/cм²;

Для дерева E= 10 ГПа.=1.10⁴МПа=1.10³кН/cм²

Потенциальная энергия не бывает отрицательной и численно равна площади диаграммы нагружения стержня (при упругой деформации площади треугольника (рис. 2.3)