7.2.Энергетические методы расчёта деформаций стержней

Практически использовать аппарат решений дифференциальных уравнений для произвольных,мрого раз статически неопределимых стержневых систем довольно трудоёмко. Кроме того, чаще необходимо иметь лишь сведения о деформациях в отдельных точках систем по фиксированным направлениям. Такую задачу успешно решает метод, предложенный Максвеллом для ферм и развитый для любых упругих систем О.Мором. Этот метод основывается на использовании принципа возможных перемещений.

В общем случае нагружения ( растяжении - сжатии, изгибе со сдвигом, кручении) в поперечных сечениях возникают внутренние усилия. Это служит причиной деформаций и накопления потенциальной энергии.

Потенциальная энергия бруса может рассматриваться как сумма независимых работ, каждого из шести

силовых факторов в сечениях, т. е. сумма энергий от каждого внутреннего усилия. Для наиболее общего подхода к воздействиям и деформациям от них введем понятия обобщенных сил и обусловленных ими обобщенных перемещениях.

Из теоретической механики известно, что если тело закреплено от смещения, то работа всех сил на возможных перемещениях равна нулю.

Деформация физического упругого тела связана с его энергетическим состоянием. Деформируемое тело способно отдавать накопленную энергию, т.е. производить работу за счёт накопленной потенциальной энергии.

Иначе, работа затраченная на деформацию, превращается в потенциальную энергию, т.е. она обратима.

Теорема Клапейрона.

Потенциальная энергия деформации в упругой системе равна половине суммы произведения обобщённых сил на обобщённые перемещения от действия всех сил.

Будем обозначать возможные перемещения с помощью индексов:

ni, где n- номер точки, в которой ищется перемещение;

i- номер точки причины, вызвавшей деформацию.

Причинами деформаций могут быть: нагрузки, изменение температуры, усадка, ползучесть, неравномерная осадка опор и т.п. Изменение или приращение потенциальной энергии связаны с произведенной дополнительной работой.

dU = dA; иначе dU - dA = 0;

Эта формулировка закона сохранения энергии выражает мысль в том, что при перемещениях внутри системы, без нарушения равновесия сумма работ всех сил равна нулю. Потенциальная энергия деформации U численно равна работе всех сил, приложенных к данному телу.

Принцип возможных перемещений: Для системы сил, находящихся в равновесии, суммарная работа этих сил на любых возможных перемещениях равна нулю.

В теоретической механике этот принцип сформулирован для твердых тел. Определению потенциальной энергии предшествует анализ внутренних силовых факторов, возникающих в брусе. Находятся величины внутренних усилий при помощи метода сечений и строятся эпюры внутренних усилий. Эпюры строятся на линии параллельной оси бруса.

Потенциальная энергия в простейших видах деформаций

Растяжение или сжатие dU (N) = ;

Сдвиг dU(Q) = ;

Кручение dU(Мk) = ;

Изгиб dU(М) = ; (7.7)

Каждому из шести силовых факторов внутренних усилий соответствует своя работа на перемещениях, а потенциальная энергия может рассматриваться, как сумма независимых шести работ.

=dU(N)+ dU(Qz)+ dU(Qy)+dU(My)+ dU(Mz)+ dU(Mk) (7.8) U= + + + + (7.9)

69

Если конструкция бруса состоит из нескольких участков или конструкций из брусьев, то после интегрирования по участкам производится суммирование энергии по числу составляющих элементов. Потенциальная энергия всегда положительна, т.к. является функцией второй степени от независимых внутренних усилий.

Теорема Кастильяно: частная производная от потенциальной энергии системы по силе равна перемещению точки по направлению этой силы.

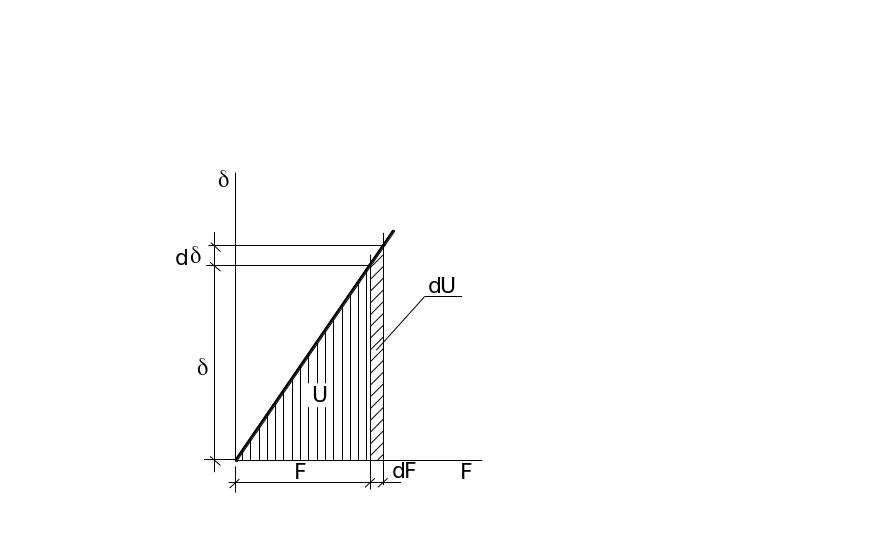
Рис.7.2.Потенциальная энергия деформации

При переходе упругой системы при изменении нагрузки меняется энергетическое состояние.

U₁=U+ dU; где dU= dF•+ 0,5d•dF (7.9)

Допустим, что величина второго порядка малости 0,5d•dF y0; тогда при изменении dU потенциальной энергии деформации, являющейся функцией сил F₁, F₂, F₃, …., произошло за счёт очень малого приращения одной из независимых переменных F_­1

=(cU/cF₁) (7.10)

70

Пример. Определить прогиб в точке приложения силы на конце консольной балки.

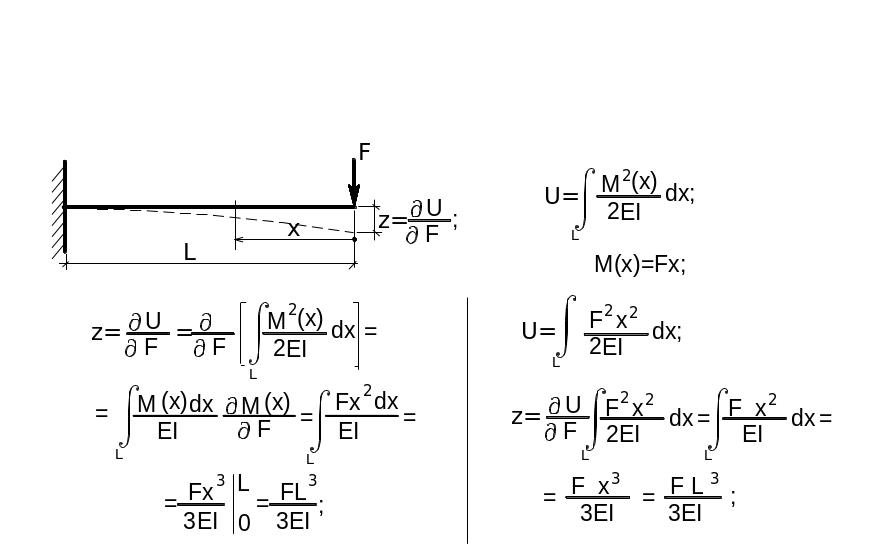
Замечание:

Производная cМ(x)/cF=-x; момент М(x)=-Fx; Обратим внимание, что cМ(x) /cF=МB(х) от F=1;

тогда прогиб:

= = = ; (7.11)

Выражение (7.11) по сути есть формула Максвелла-Мора. Если необходимо определить перемещение в точке, в каком либо направлении, где не приложена внешняя нагрузка, то необходимо приложить фиктивную силу Ф, в интересующем нас направлении. Тогда изгибающий момент в брусе будет:

М=М­_F+M_Ф (7.12)

Cилу Ф можно представить как M₁• Ф, а потенциальную энергию:

U= = (7.13)

(7.13) продифференцируем по Ф

=  (7.14)

(7.14) – Интеграл Максвелла – Мора. Вычисление перемещения сводится интегралу от произведения эпюр изгибающих моментов, от сдвига, растяжения-сжатия и кручения. Т.е. перемещение является суммой всех воздействий (всех видов деформаций) от обобщенной силы:

= + + + + + (7.15)

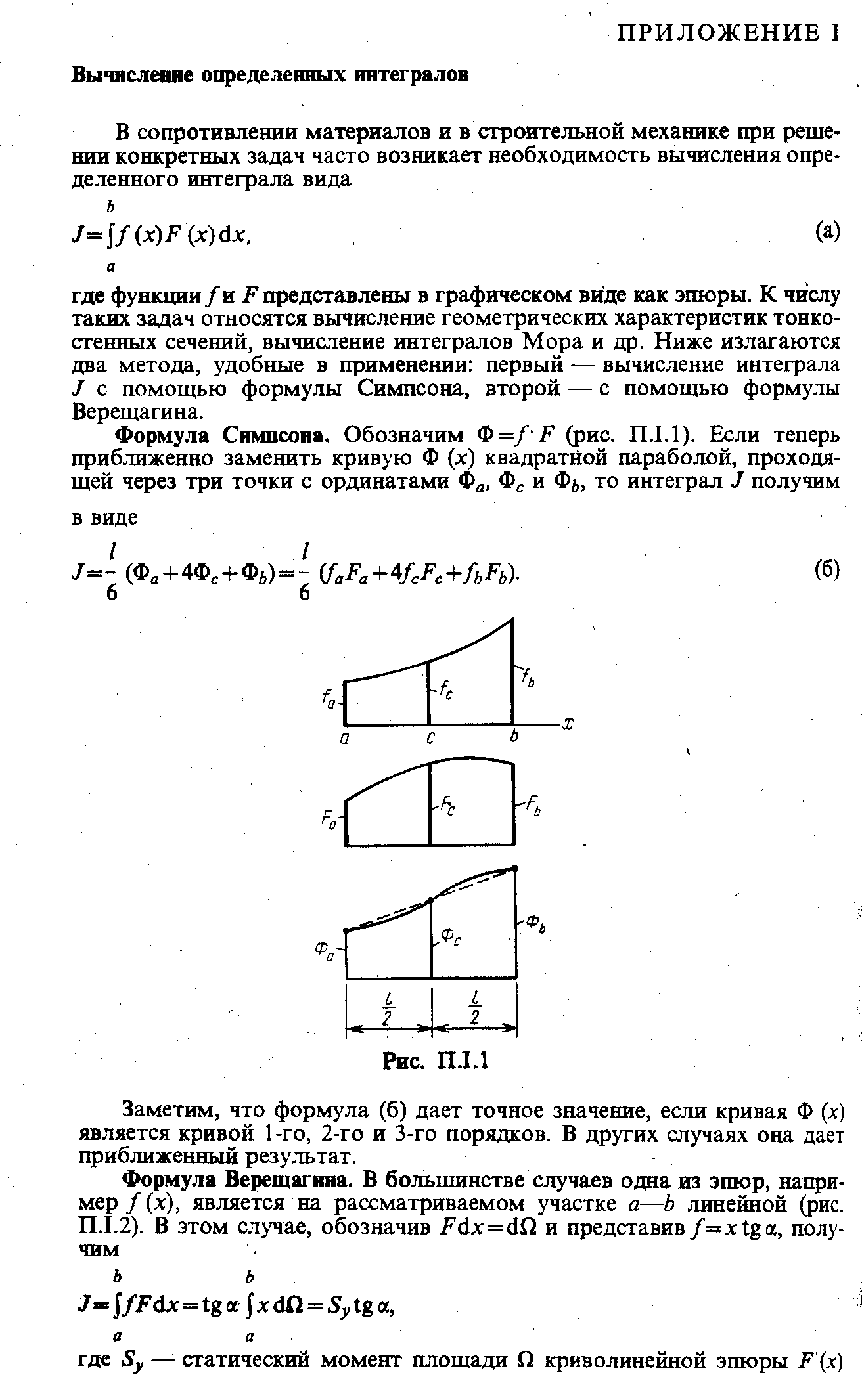
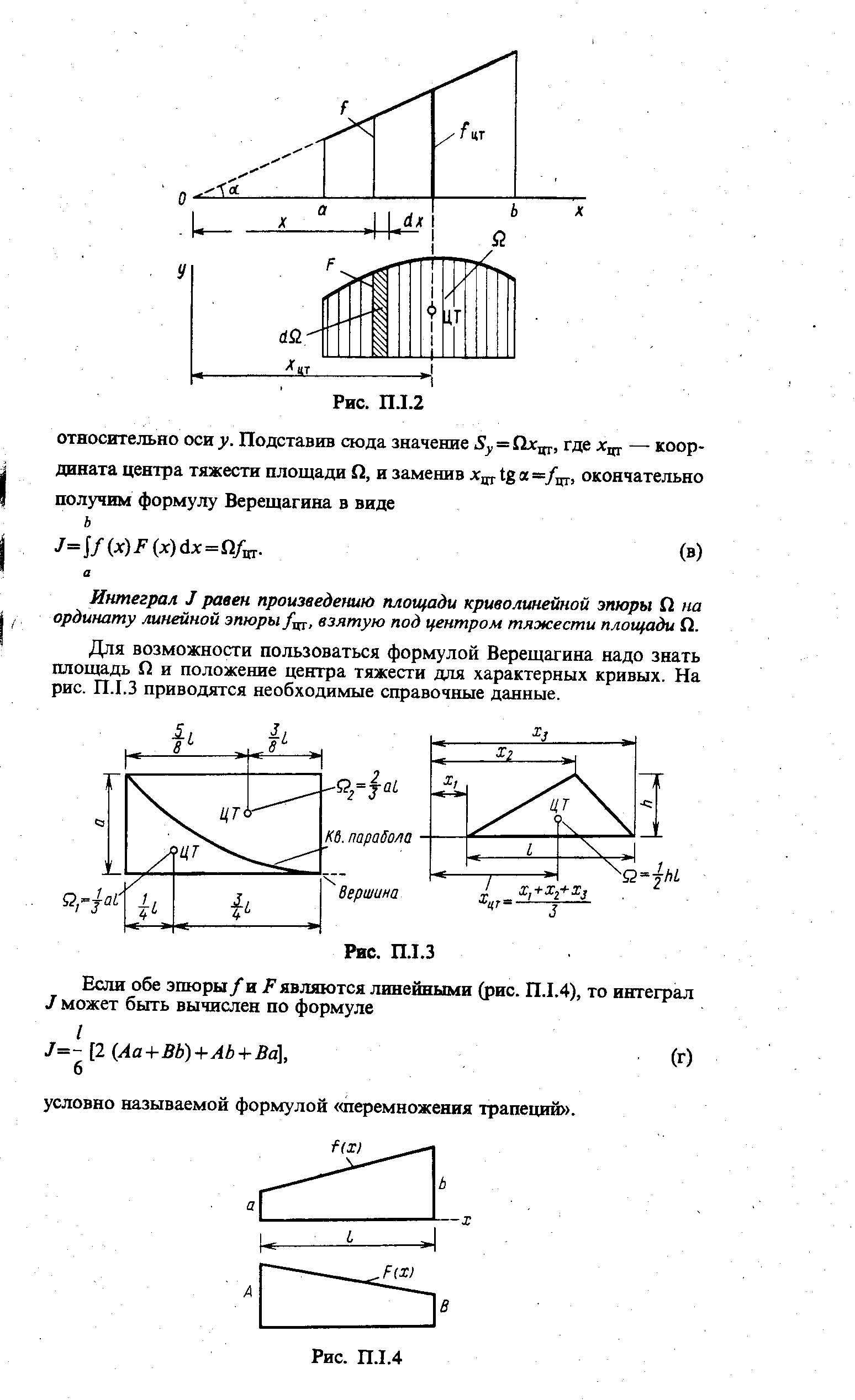
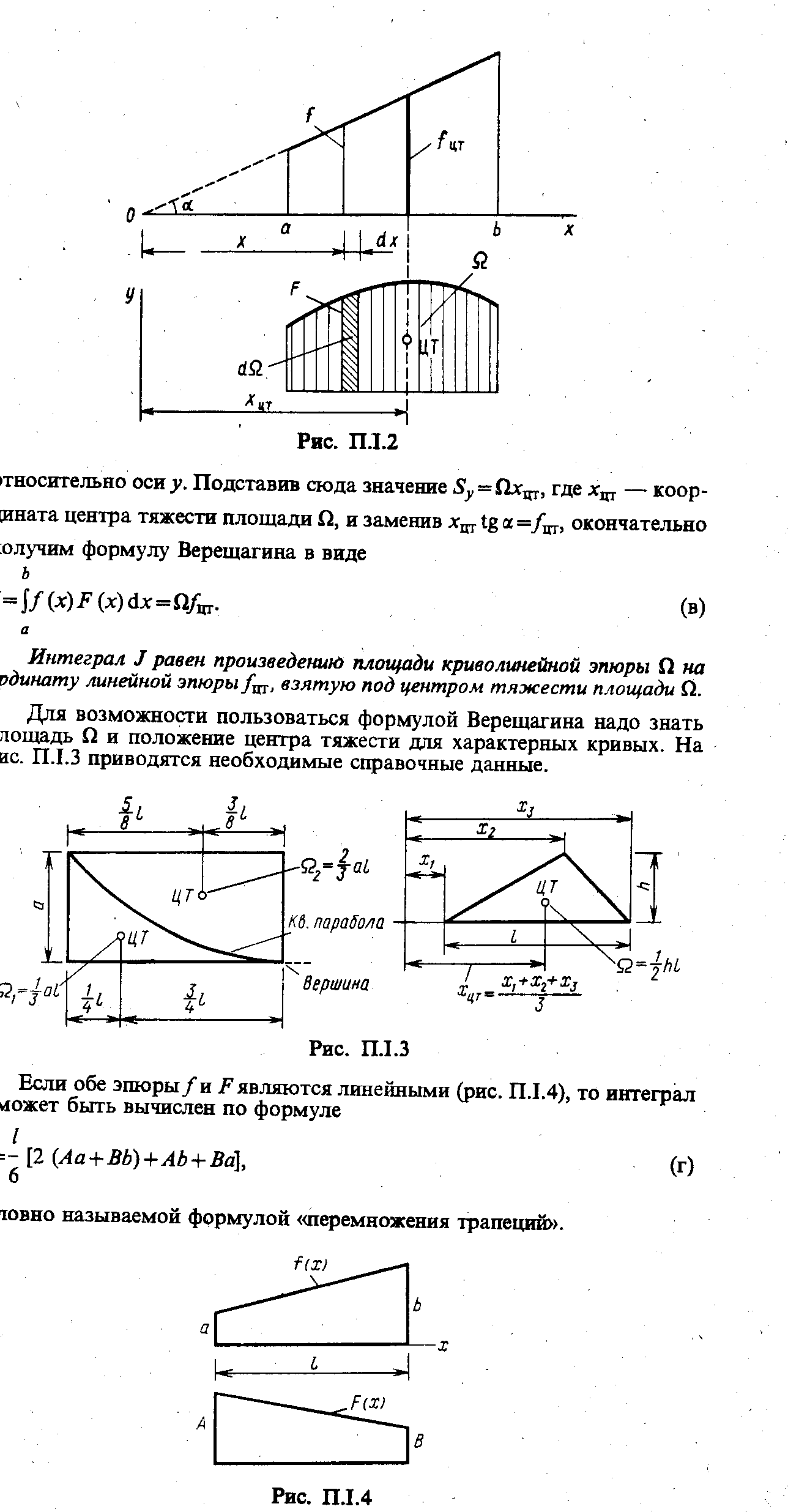
Вычисление определённых интегралов

71

72

73

Пример: Определить прогиб.

.

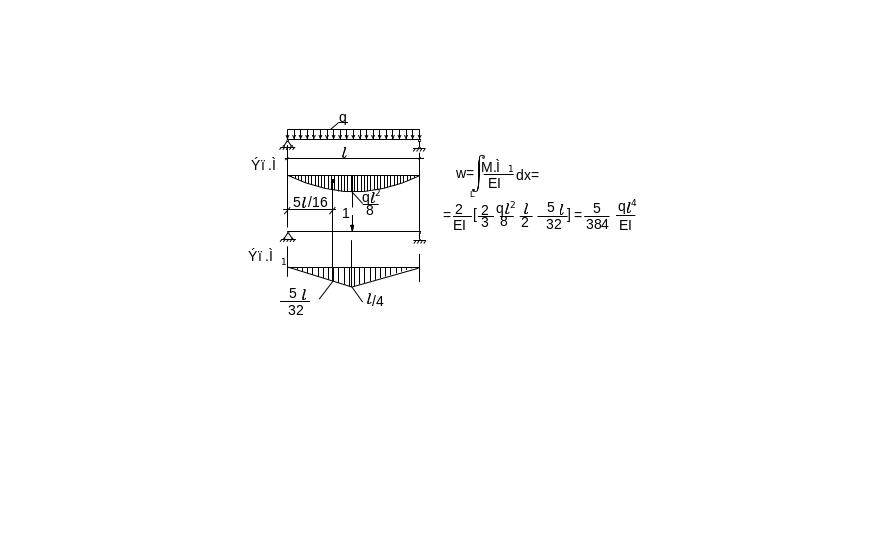
74