6.6.Понятие о центре изгиба

Если равнодействующая поперечной нагрузки в сечении проходит через центр изгиба, то недолжно возникать кручения.

Точка приложения равнодействующей касательных сил в поперечном сечении при изгибе без кручения наз центром изгиба.

Для сечения, имеющего две оси симметрии, центр изгиба лежит на пересечении этих осей, т.е. совпадает с центром тяжести сечения. В других случаях эти точки не совпадают.

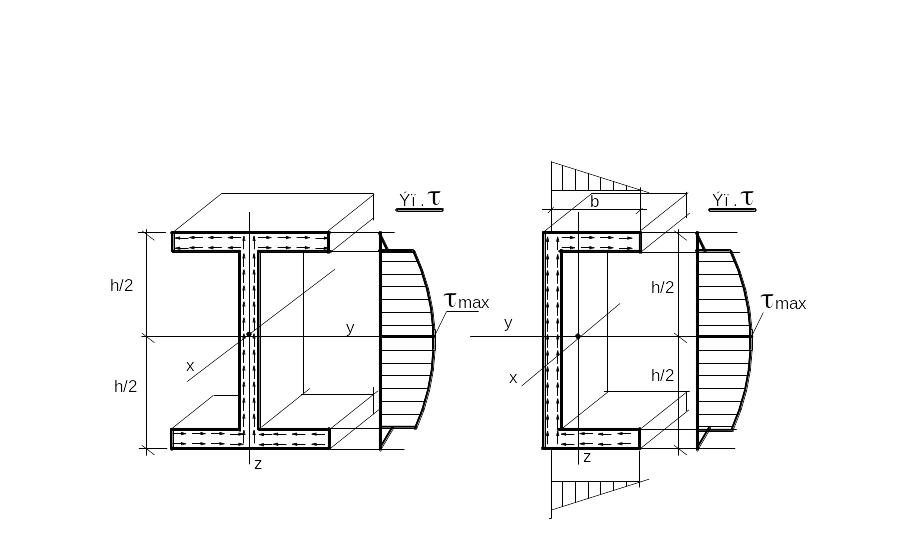
Рис. 6.12. Касательные напряжения в сечениях тонкостенных балок при поперечном изгибе:

а)в двутавровой; b) в швеллере

Знание положения центра изгиба необходимо для предотвращения деформации кручения. Стержни открытого профиля слабо сопротивляются кручению. В качестве примера найдём центр изгиба для швеллера рис.6.13. В полках от изгиба возникают в вертикальной плоскости (по площадкам с нормалью «х»)горизонтально направленные касательные напряжения, направленные вдоль оси «у».

63

Сумма моментов относительно точки О.

M_o=0; T_y•h-T_­z•=0; = T_y•h/ T_­z; T_­z=Q;

_xz=Q S^отс /(b Iy)=Q•(b••0,5h)/(•_y) =0,5•Q• b• h/_y;

_yy2• b••(h/2)²+_СТ• h³/12; =3b/(6+h•_СТ/(b•);

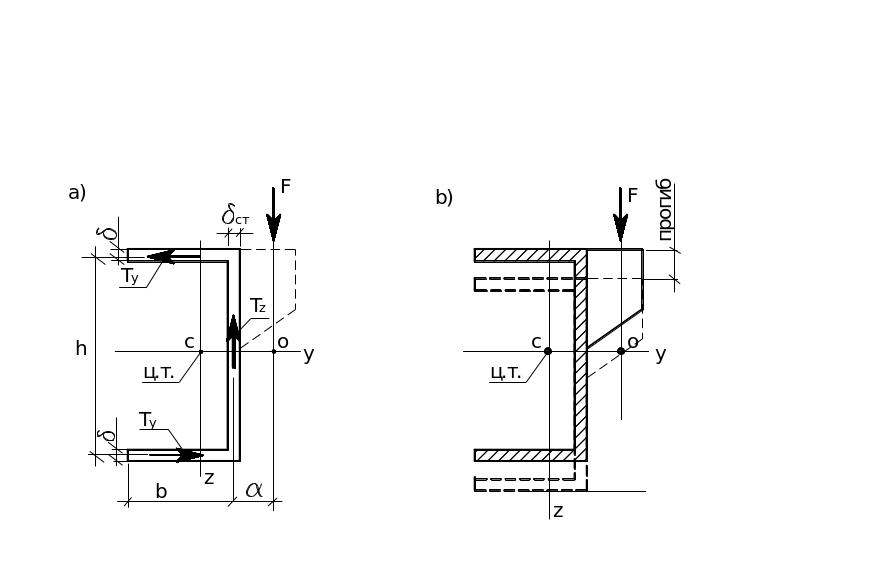
Рис. 6.13. Определение положения центра изгиба (кручения) тонкостенного профиля типа швеллера

64

7. Перемещения при изгибе

При действии внешних сил балка изменяет кривизну. При этом каждое сечение получает два перемещения: линейное - прогиб и угловое -угол поворота сечения (рис. 7.1).

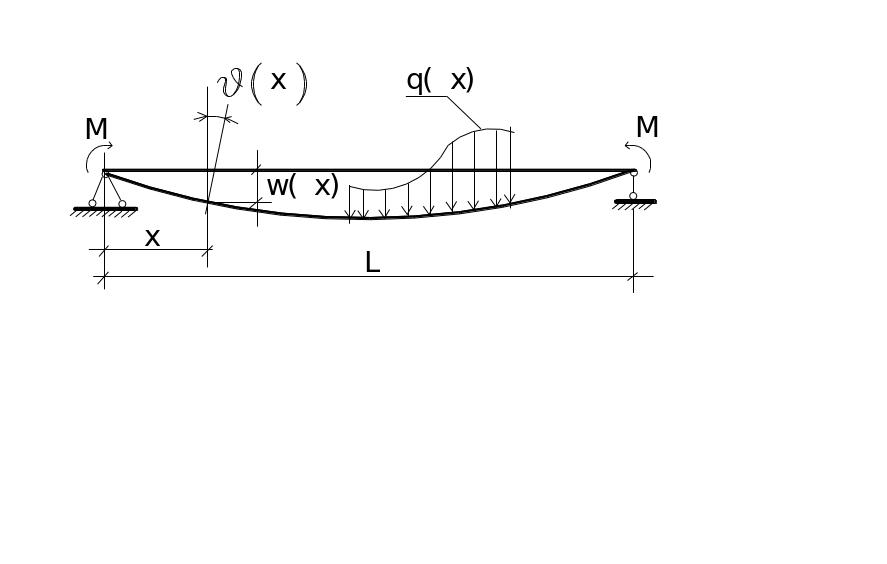
7.1. Перемещения балки при изгибе

При проектировании нормы ограничивают прогибы, т.е. требуют обеспечения жесткости конструкций для обеспечения эксплуатационной пригодности. При расчете статически неопределимых конструкций возникает необходимость в составлении дополнений к уравнениям статики. Обычно такими служат уравнения совместных деформаций.

Основной вклад в деформацию изгиба вносят изгибающие моменты, вызывающие искривление каждого элемента балки длиной dx, а деформациями сдвига от поперечных сил обычно пренебрегают из-за их малости. Прогибом наз. перемещение центра тяжести сечения в направлении вертикальной оси w(x). По сути уравнение w(x) является уравнением упругой линии балки или линией прогибов.

Угол поворота по сути угол наклона касательной к линии прогибов. Согласно гипотезе плоских сечений, каждое сечение остаётся нормальным к оси, т.е. можно считать его и углом поворота сечения.

tg (x)= wB(x) (7.1)

При малых углах поворота tgy, поэтому имеем простую зависимость. Такая модель носит название Эйлера-Бернулли.