5.2.Потенциальная энергия при чистом сдвиге

Работу совершает касательная сила Q на грани элемента, длиной равной 1. Q= •h• 1 на перемещении .

А=0,5 Q =0,5γ h² и τ=Gγ (5.11)

Отнесем эту работу к единице объёма U=A/( h²•1)= 0,5γ h²/( h²•1)=0.5 G γ² (5.12)

где U-плотность энергии деформации сдвига или удельная потенциальная энергия.

44

5.3.Кручение стержней круглого поперечного сечения. Касательные напряжения и угол закручивания

Стержень нагружен только парами сил, вращающих стержень вокруг продольной оси x. При этом в поперечных сечениях стержня действует только одно внутреннее усилие- крутящий момент, Mк=Mx, численно равный сумме моментов всех сил, расположенных по одну сторону от рассматриваемого сечения.

Знак крутящего момента обычно безразличен, так как прочность стержня при кручении зависит только от величины крутящего момента и не зависит от его направления. Тем не менее, для упорядочения расчетов в ряде учебников рекомендуется считать крутящий момент положительным, если при взгляде со стороны любого конца стержня мы видим внешний закручивающий момент, действующим против часовой стрелки.

В технике наиболее часто используются стержни круглого или кольцевого поперечного сечения. Оказывается и расчет таких стержней на кручение значительно проще, чем стержней с другой формой поперечного сечения. С этого случая и начнем изучение деформации кручения стержней.

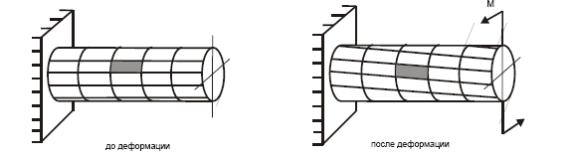
Рис. 5.3. Деформация при кручении стержня с прямоугольной сеткой

Рассмотрим результат следующего эксперимента. На поверхность резинового стержня круглого поперечного сечения нанесем прямоугольную сетку (рис. 5.3).

Нагрузим стержень парой сил, закручивающей стержень вокруг продольной оси. При этом поперечные сечения стержня поворачиваются относительно друг друга, и нанесенная сетка линий искажается. Первоначально прямоугольные элементы сетки становятся параллелограммами.

Изменение формы элемента сетки свидетельствует о деформациях сдвига, происходящих при кручении стержня круглого сечения.

Основные гипотезы

Вывод формул для напряжений и перемещений при кручении начнем с гипотез, принимаемых для упрощения расчетов.

Итак на гранях элемента стержня, вырезанного плоскостями, перпендикулярными осям x, отсутствуют нормальные напряжения-σ и действуют только касательные τ (рис.5.4). Такой случай напряжения называется чистым сдвигом. Следовательно, кручение-частный случай чистого сдвига и все зависимости, полученные при рассмотрении деформации сдвига, могут быть использованы при кручении стержней.

45

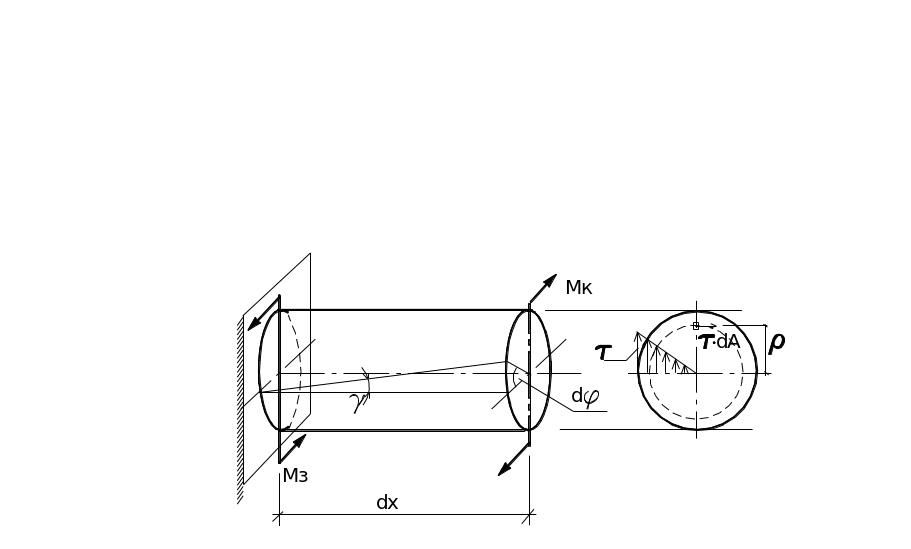
Рис.5.4.Деформация элемента стержня при кручении

Относительный угол закручивания = d/dx; τ= γ G;

Изменение угла поворота сечения происходит за счет сдвигов, при этом в сечении возникают касательные напряжения . Cоставим уравнение равновесия в сечении относительно оси х.

Мк– ∫ •dA•

^A

Мк  A∫ G (d/dx) d=G (d/dx) ∫² dA

d/dx= Мк./( GIp); = Мк•L/( GIp) ; 

τ= γ G; τ= Мк• ./Ip; τmax= Мк•r./Ip= Мк/Wp 

  

Если на стержень действуют несколько внешних нагрузок, то сумма берется по числу участков n на стержне. Границами участков являются сечения, где либо приложены нагрузки, либо изменяются форма и размеры поперечного сечения.

6

Где l- длина соответствующего участка.

46