4.2.2. Моменты инерции сечений относительно параллельно перенесённых осей
Пусть известны моменты инерции относительно центральных осей 0z и 0y для сечения площадью A. Найти моменты инерции относительно осей z1 и y1, перенесенных параллельно 0z и 0y на расстояния a и b.
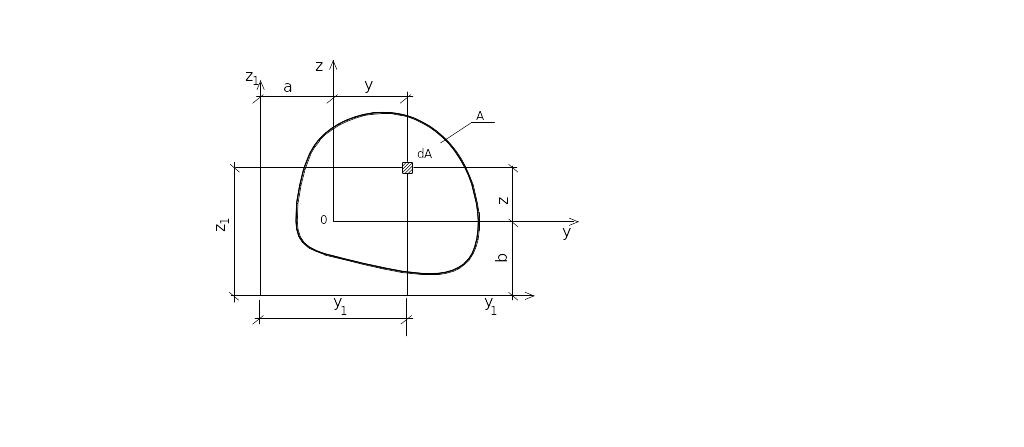
Рис.4.6. Схема к преобразованию осевых моментов инерции при параллельном переносе
координатных осей
Пусть известны геометрические характеристики сечения относительно осей y и z , которые параллельны y1 и z1. Координаты в новой систем y1=y+a ; z1 =z+b.
(4.14)
Аналогично получим формулу относительно Z1
(4.15)
Для центробежного момента инерции
Для исходных моментов инерции, определённых относительно центральных осей Sy=0 и Sz=0.
(4.16)
Последние формулы называют переходными от центральных осей к любым параллельным.
4.2.3. Моменты инерции сечений при повороте осей, главные оси
Будем считать, что моменты инерции относительно осей y и z известны
.
(4.17)
40
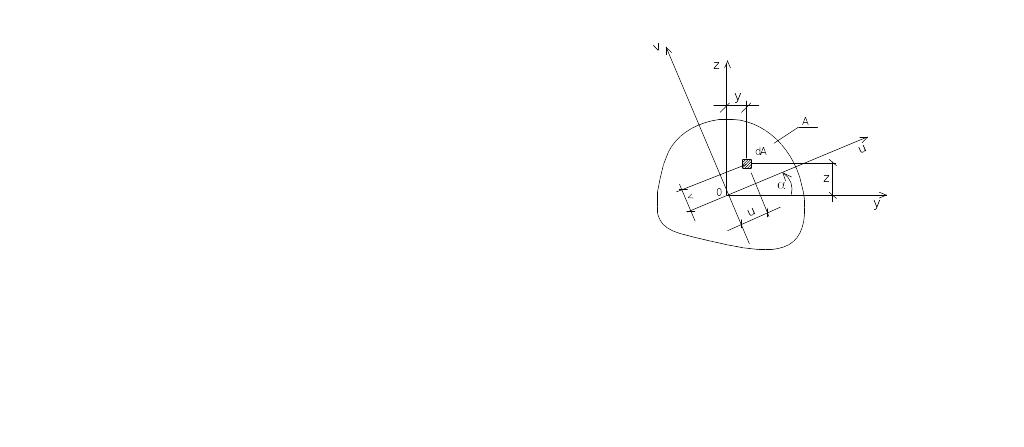
Рис.4.7. Схема к выводу зависимостей моментов инерции при повороте осей
Запишем новые координаты элементарной площадки dA.
(4.18)
Подставим (4.18) в (4.17)
;
(4.19)
;
(4.20)
Отметим, что
,
поэтому
.
Теперь получим центробежный момент
инерции
;
(4.21)
Для удобства при вычислениях формулы (4.19) и (4.20) можно привести тригонометрическим преобразованием
к виду
(4.22)
Главные оси характеризуются экстремальным значением осевых моментов инерции и равенством нулю центробежного.
=0;
41
Угол наклона
главных осей к ортогональным
(4.23)
По этой формуле
определяются два значения угла
и
+90°
и положение главных
осей, которые являются взаимно
перпендикулярными. Значения осевых
моментов инерции относительно главных
осей являются экстремальными.
;
(4.24)
Верхний знак «+» соответствует максимальному моменту инерции, а нижний «–» минимальному.
Очевидно, по аналогии с напряжённым состоянием, можно заключить, что изменение осевых моментов с центробежным можно изобразить в виде круга Мора.Часто вместо формулы (4.23) используют определение положения главных осей по выражениям (4.25):
(4.25)
–угол
между осью y
и осью, относительно которой момент
инерции равен
,
а угол
угол
между осью z
и осью, относительно которой
.
42