CПбГАСУ

Кафедра «Сопротивления материалов»

Сопротивление материалов

Краткий конспект лекций

Часть I

Доц. Рощин В.В.

Санкт-Петербург

2009г.

1

Предисловие

Краткий конспект лекций по сопротивлению материалов предназначен для специальностей с сокращённой программой для бакалавров и дипломированных специалистов. Это направление специалистов должно получить знания о принципах и методах расчетов на прочность, жесткость и устойчивость простейших элементов систем при нагружении и иметь опыт в таких расчетах.

Примерное количество часов :

Общая трудоемкость дисциплины	114/165
Аудиторные занятия	64/95

С одним экзаменом или зачётом. Это так называемая группа- блок 2.

Разделы дисциплины и виды занятий (кол. Часов)

№ п/п	Раздел дисциплины	Лекции	Практические	Кол. работ
1.	Введение	2	-	-
2.	Центральное растяжение-сжатие	4	6	1
3.	Сдвиг	2	-	-
4.	Геометрические характеристики поперечных сечений стержня	2	2	-
5.	Прямой поперечный изгиб	5	7	2
6.	Кручение	3	3	1
7.	Косой изгиб и внецентренное растяжение-сжатие	2	3	1
8.	Напряженное и деформированное состояние в точке тела	2	2
9.	Теории прочности	3	3	-
10.	Устойчивость сжатых стерней	3	4	-
11.	Расчет на прочность при циклически меняющихся во времени напряжениях	2	-	-

2

1.Введение

1.1.Основные понятия

Сопротивление материалов – наука, изучающая поведение материалов (физических тел),

при нагрузках, силовых и др. воздействиях. Обеспечивает прочность, жесткость, устойчивость и эксплуатационную пригодность элементов конструкций и сооружений, при минимуме затрат.

Сопротивление материалов является разделом механики, а основу его составляют:

-физика твердого тела;

-механика деформирования сплошных сред.

Прочность- способность материала конструкции сопротивляться внешним воздействиям.

Жесткость- способность элементов конструкций сохранять исходную форму в допустимых пределах.

Устойчивость – способность конструкций сохранять первоначальную форму равновесия.

Надёжность- обеспечение безопасной эксплуатации и работоспособности элементов конструкций.

   Согласно ГОСТ 27.002—89 «Надежность в технике. Термины и определения» надежность конструкции есть свойство сохранять во времени способность к выполнению требуемых функций в заданных режимах. Одним из основных понятий теории надежности конструкций является понятие предельного состояния. Условие прочности по существу есть условие обеспечения прочностной надежности.

Долговечность- обеспечение нормированного срока службы сооружения или конструктивного элемента.

Сопротивление материалов опирается на созданные этой наукой расчетные схемы

реальных объектов, сведения о свойствах материалов, теоретическую механику, математику (статистические методы обработки экспериментов, дифференциальное и интегральное исчисления и др.),

Расчётная схема, представляющая реальный объект, отличается от последнего схематизацией и упрощением свойств материалов, нагрузок и способов закрепления объектов. В процессе решения задачи подбираются надежные размеры сечений элементов конструкций или проверяется надежность уже существующей (подбор сечения или проверка прочности). Т.е. расчетная схема является математической моделью реального объекта, у которого отброшены несущественные свойства, позволяющие решить задачу относительно несложными математическими способами.

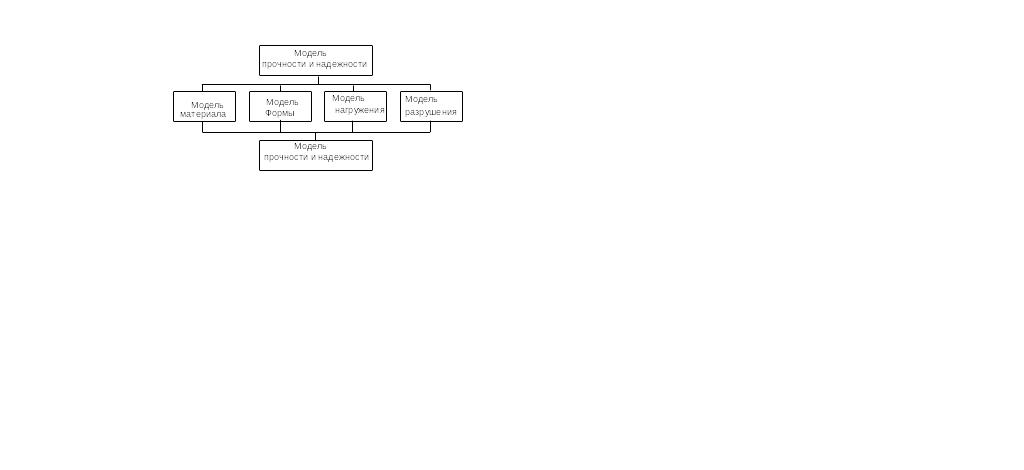
3

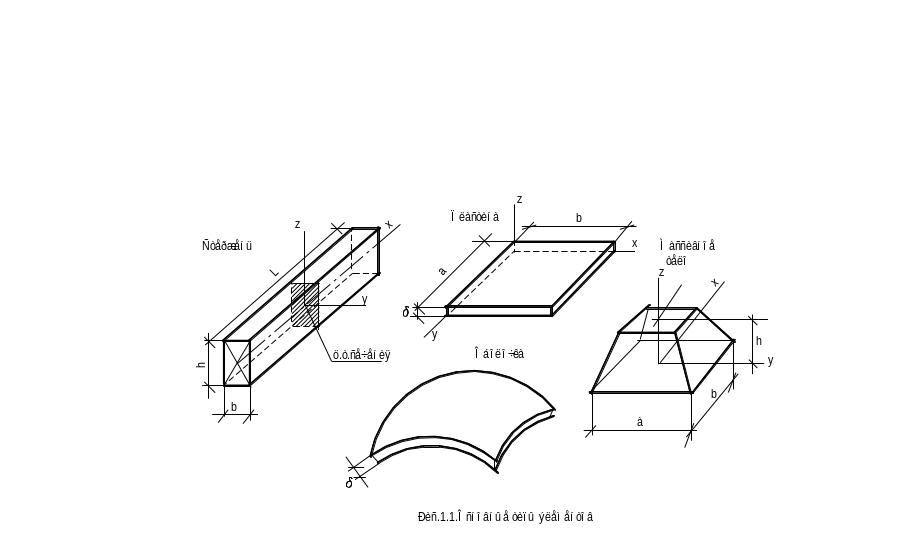
Применение методов в сопротивлении материалов ограничивается расчетами отдельных элементов (стержень, балка, пластинка, оболочка, массивное тело, балка на упругом основании, рама, ломаный стержень, соединительные элементы, пружины и т.п.).

. 1.2. Внешние и внутренние силы

Внешние нагрузки или силы и моменты являются результатом давления поверхностей элементов

с внешней стороны тел или воздействия с другими явлениями ( снег, ветер, сейсмика, инерционные нагрузки, силы гравитации, температурными колебаниями внешней среды, нагрузками от оборудования, от скопления людей, колёсные и гусеничные нагрузки транспорта, давления грунтов и жидкостей и т.п.).

Поверхностная нагрузка характеризуется:

- величиной, определяемой главным вектором и главным моментом от суммы вех сил и моментов; интенсивностью, величиной отнесённой к единице площади или единице длины для равномерно распределённой нагрузки

q = F /w [ МПа, кПа, Па] (1.1)

q = F /L [ МН/м, кН/м, Н/м] (1.2)

q – интенсивность нагрузки; F – величина нагрузки; w – площадь приложения нагрузки, L – длина

участка приложения нагрузки.

Нагрузка может быть не равномерно распределённой, тогда говорят об интенсивности в точке с координатами, изменяющейся по закону qz=q(x,y):

q(x,y) = [ МПа, кПа, Па] (1.3)

Интенсивность поверхностной нагрузки в общем случае определяется как предел отношения равнодействующей сил на рассматриваемом участке к её площади,стремящейся к нулю.

Величина равнодействующей нагрузки по площадке w связана с интенсивностью соотношением

(см. рис.1.2): F = q(х,у) dх dу (1.4)

Момент от такой нагрузки относительно оси х будет:

4

М_х = (1.5) .

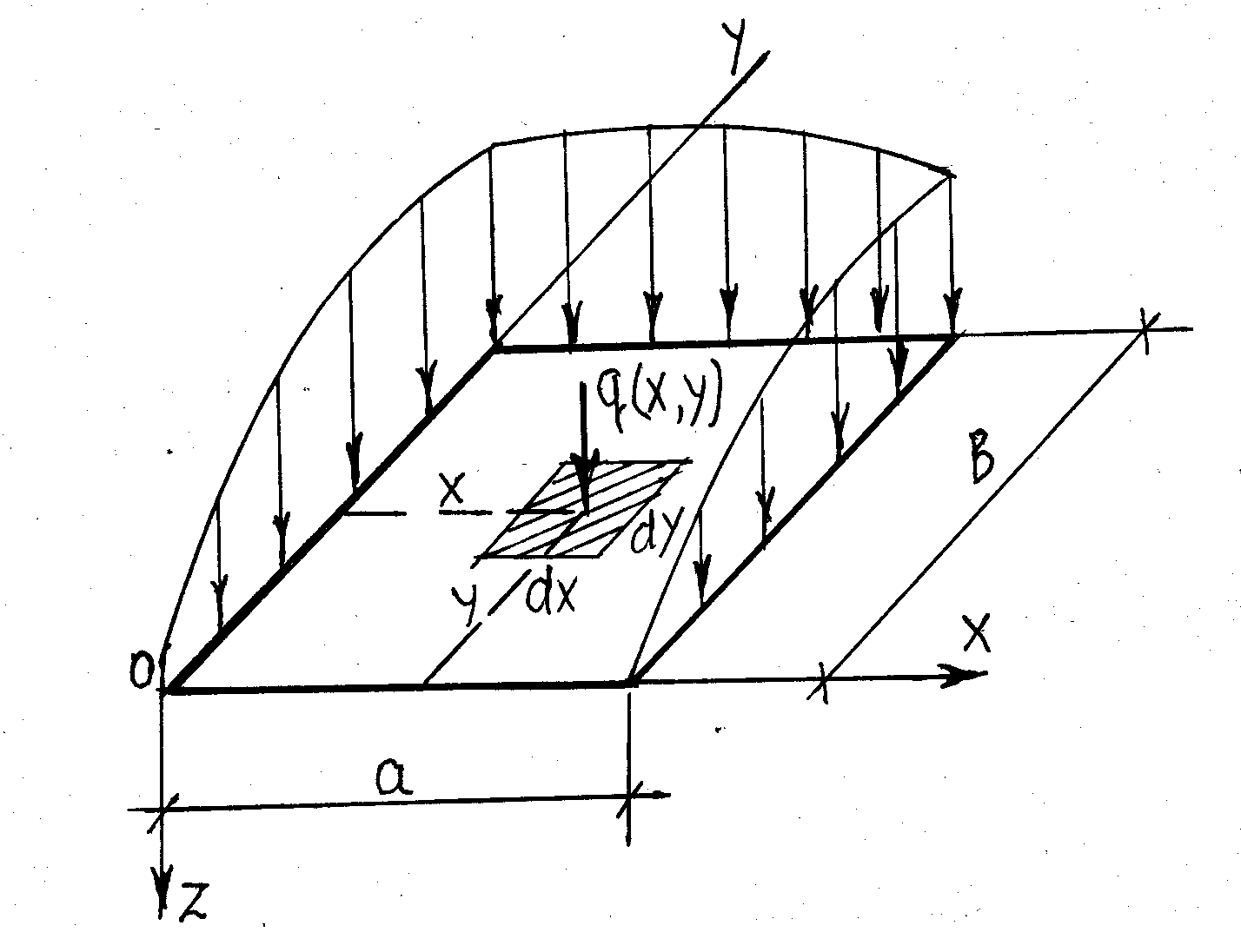
Рис.1.2.Схема к определению действия распределенной нагрузки

Правило знаков: при совпадении направленности вектора нагрузки с направлением соответствующей оси координат знак «+».

Реакции связей относятся к внешним поверхностным силам. В задачах со статическими силами реакции находятся из условий равновесия рассматриваемого тела.

SX=0; SY=0; SZ=0;

SMx=0; SMy=0; SMz=0. (1.6)

Все нагрузки передаются на физические тела через некоторые площадки. Если размеры площади для передачи нагрузки малы, то последние можно представить в расчетной схеме в виде сосредоточенной силы, приложенной в точке (рис.1.3).

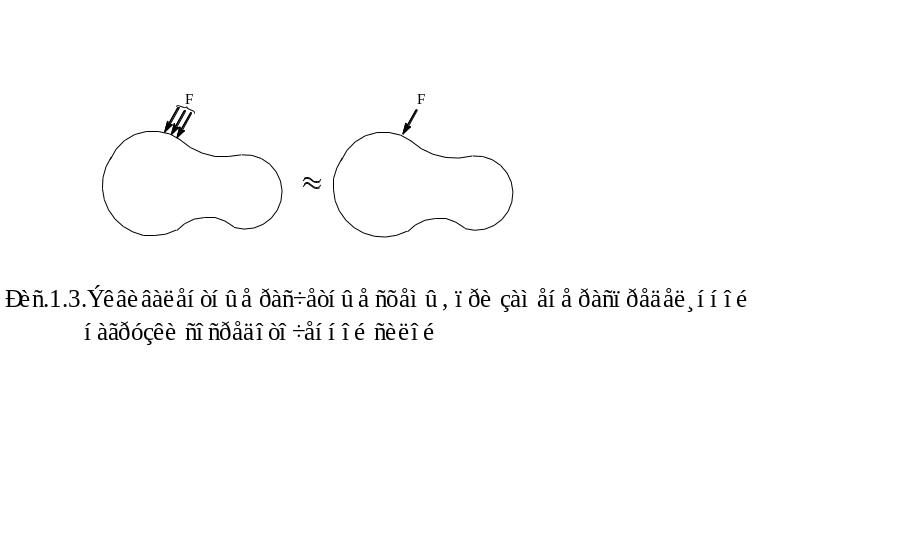
Помимо нагрузок поверхностных , существуют такие, которые приложены к любой части объёма. Их называют объёмными. Например, силы гравитации или собственный вес тела, силы инерционные и т.п.

При составлении уравнений равновесия необходимо знать точку, в которой расположена равнодействующая распределенной нагрузки (см. Рис.1.4).

5

Рассмотрим два случая распределения нагрузки:

- для равномерно распределённой линейной нагрузки:

F=q a; точка приложения . (1.7)

• для изменяющейся линейно (по закону прямой линии):

; (1.8)

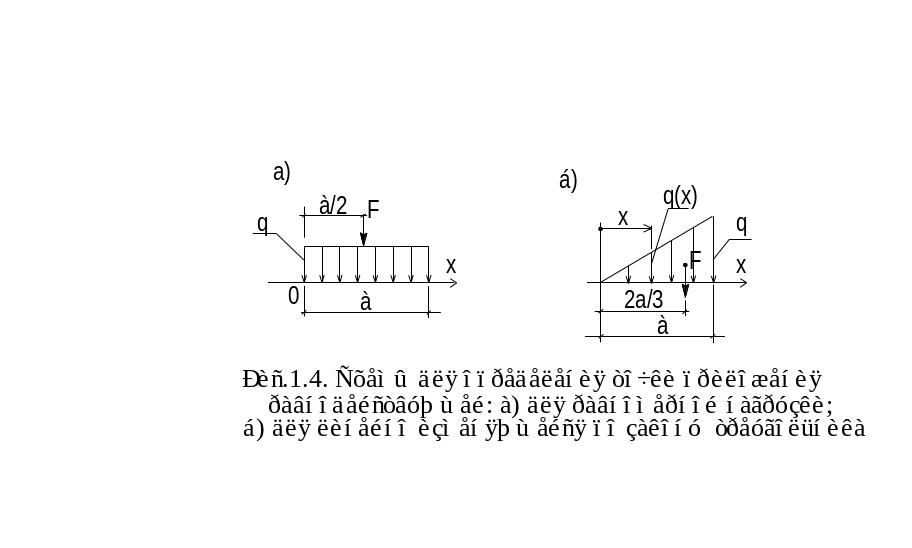
В обоих случаях точка приложения равнодействующей совпадает центром площади нагрузки. Классификация нагрузок и воздействий для строительных целей приводится в нормах проектирования

СНиП 2.01.07-85* «Нагрузки и воздействия». Нагрузки в зависимости от продолжительности действия

различают как постоянные и временные (длительные, кратковременные, особые).

Отдельно учитывают нагрузки, возникающие при изготовлении, хранении и транспортировании.

По характеру действия различают статические нагрузки и динамические, вызывающие значительные ускорения и инерционные воздействия.

Под действием внешних сил всякое физическое тело изменяет форму и размеры, т.е. возникают изменения, которые называют деформациями.

Различают деформации:

а) упругие, т.е. обратимые, полностью исчезающие после снятия нагрузки;

б) остаточные, т.е. необратимые, не исчезающие после прекращения действия нагрузок.

Разрушение материала в виде трещин, отколов и т.п. влечёт за собой появление остаточных деформаций.

Остаточная деформация, не сопровождающаяся местными разрушениями наз. пластической.

Мысленно рассекаем тело произвольным сечением (рис. 1.3, а), отбрасываем одну часть тела и рассматриваем равновесие оставшейся части. Если бы не было внутренних сил, оставшаяся неуравновешенная часть тела начала бы двигаться под действием внешних сил. Поскольку сечение мысленное и тело находится в равновесии, действие отброшенной части тела заменяем внутренними силами (рис. 1.3, б), приложенными к каждой частице тела. Из теоретической механики известно, что любая система

6

сил может быть приведена в любую точку пространства в виде главного вектора сил и главного момента сил RM (рис. 1.3, в). Модуль и направление этих векторов неизвестны. Удобнее всего определять проекции этих векторов на оси x,y,z, где ось х - нормаль к сечению, y и z –ортогональные оси, лежащие в плоскости сечения. Начало координат в центре тяжести сечения (рис. 1.3, г). Дадим название внутренним усилиям .

Проекции векторов:

N-продольное усилие по оси х;

поперечные усилия, соответственно вдоль осей с аналогичными индексами;

крутящий момент;

изгибающие моменты вокруг осей у и z.

В общем случае определения внутренних усилий имеется шесть уравнений с шестью неизвестными.

SFx=0; для Nx,

SFy=0; для Qy ,

SFz=0; для Qz ,

SM(F)x=0; для Mx, (1.10)

SM(F)y=0; для My,

SM(F)z=0; для Mz,

Внутренние усилия могут изменяться по величине и направлению. Диаграммы(графики) изменения

величины внутреннего усилия по длине наз. эпюрами.